
题目列表(包括答案和解析)
17、(14分)一个总体中的1000个个体编号为0,1,2,…,999,并依次将其分为10个小组,组号为0,1,2,…,9,要用系统抽样方法抽取一个容量为10的样本,规定如果在第0组随机抽取的号码为x,那么依次错位地得到后面各组的号码,即第k组抽取的号码的后两位数是x+33k的后两位数。
(1)当x=24时,写出所抽样本的10个号码;
(2)若所抽取样本的10个号码中有一个的后两位是87,求x的取值范围。
16、(14分)某校参加高考学生1500人,该次考试服从平均数为65,标准差为15的正态分布,试问在60分以下的有多少人?
(二)填空题(每小题6分,共30分)
11、正态曲线 (
( >0,-∞<x<+∞)的对称轴是____________。
>0,-∞<x<+∞)的对称轴是____________。
12、从1000件新产品中抽取20件检查,采用系统抽样的方式,应将总体分成______部分。
13、正态总体N(μ, 2)在区间(μ-3
2)在区间(μ-3 ,μ+3
,μ+3 )内取值的概率是________。
)内取值的概率是________。
14、一个容量为n的样本分成若干组,已知某组的频数和频率分别为80和0.125,则n=__________。
15、一个工作有若干个车间,今采用分层抽样的方法从全厂某天的2048件产品中抽取一个容量为128的样本进行质量检验,若某一车间这一天生产256件产品,则从车间抽取的产品件数为________。
(一) 选择题
1、为了调查全国人口的寿命,抽查了十一个省市的2500名城镇居民,则该问题中的2500名城镇居民是:
A、总体 B、个体 C、样本 D、样本容量
2、一个容量为100的样本分成若干组,已知某组的频率为0.4,则该组的频数是:
A、4 B、40 C、10 D、400
3、利用简单随机抽样从含有6个个体的总体中抽取一个容量为3的样本,则总体中每个个体被抽到的概率是:
A、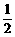 B、
B、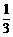 C、
C、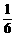 D、
D、
4、如果x-N(μ, 2),则( )-N(0,1):
2),则( )-N(0,1):
A、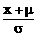 B、
B、 C、
C、 D、1
D、1
5、如果提出统计假设,某学生数学成绩x服从正态分布N(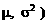 。下列哪种情况下可以说假设不成立:
。下列哪种情况下可以说假设不成立:
A、 B、
B、
C、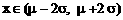 D、
D、
6、如图是一批产品中抽样得数据在频率分布图,从图中可以看出数据所落在范围的频率最大的是:
 A、(8.1,8.3) B、(8.2,8.4) C、(8.4,8.5) D、(8.5,8.7)
A、(8.1,8.3) B、(8.2,8.4) C、(8.4,8.5) D、(8.5,8.7)
7、一个容量为20的样本,分组后,组距与频数如下:
|
组距 |
(10,20) |
(20,30) |
(30,40) |
(40,50) |
(50.60) |
(60,70) |
|
频数 |
2 |
3 |
4 |
5 |
4 |
2 |
则样本在区间(-∞,50)上频率为:
A、5% B、25% C、50% D、70%
8、 三条正态曲线对应的标准差分别为
三条正态曲线对应的标准差分别为 1,
1, 2,
2, 3,如图,则:
3,如图,则:
A、 1>
1> 2>1>
2>1> 3 B、
3 B、 1>
1> 2=1>
2=1> 3
3
C、 3>
3> 2>1>
2>1> 1 D、
1 D、 3>
3> 2=1>
2=1> 1
1
 9、如图是正态分布N(0,1)的正态曲线图,下面4个式子中,能表示图中阴影部分面积的个数为:
9、如图是正态分布N(0,1)的正态曲线图,下面4个式子中,能表示图中阴影部分面积的个数为:
①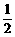 -
- (-a) ②
(-a) ② (-a)
(-a)
③ (a)-
(a)-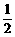 ④
④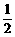 [
[ (a)-
(a)- (-a)]
(-a)]
A、1个 B、2个 C、3个 D、4个
10、利用随机抽样从含有12个个体的总体中抽取一个容量为4的样本,设个体a被抽到的概率为P1,个体a没有在第二次抽到的概率为P2,则P1与P2的大小关系是:
A、P1>P2 B、P1=P2 C、P1<P2 D、不确定
例1、写出抽样过程:从拥有500个分数的总体中用简单随机抽样方法抽取一个容量为30的样本。
解:①将总体的500个分数从001开始编号,一直至500号;
②从随机数表第1页第0行至第2页第4列的758号开始使用该表;
③抄录入样号码如下:335,044,386,446,027,420,045,094,382,215,342,148,407,349,322,027,002,323,141,052,177,001,456,491,261,036,240,115,143,402;
④按以上编号从总体中将相应数取出组成样本,即可。
例2、求正态总体在下面区间取值的概率。
(1)已知:x-N(0,1),求P(-1<x<2),P(x>2);
(2)已知x-N(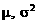 ),求F(μ-1.96
),求F(μ-1.96 ,μ+1.96
,μ+1.96 )。
)。
解:(1)P(-1<x<-2)= (2)-
(2)- (-1)=
(-1)= (2)-[1-
(2)-[1- (1)]=
(1)]= (2)+
(2)+ (1)-1
(1)-1
=0.9773+0.8413-1=0.8186
P(x>2)=1- (2)=1-0.9773=0.227
(2)=1-0.9773=0.227
(2)∵ F(μ+1.96 )=
)= (
( )=
)= (1.96)
(1.96)
F(μ-1.96 )=
)= 
 =
= (1.96)=1-
(1.96)=1- (1.96)
(1.96)
∴ F(μ-1.96 ,μ+19.6
,μ+19.6 )=2
)=2 (-1.96)-1=0.95
(-1.96)-1=0.95
例3、某年级的一次信息技术测试成绩近似服从正态分布N(70,100),如果规定低于60分为不及格,不低于85分为优秀,那么:
(1)成绩不及格的学生约占多少?
(2)成绩优秀的学生约占多少?
解:依题意,求题得分少于60分的学生的比为F(60),少于85分的学生的比为F(85)
(1)F(60)= (
( =
= (-1)=1-
(-1)=1- (1)=1-0.8413=0.1587
(1)=1-0.8413=0.1587
(2)F(85)= 
 =
= (1.5)=0.9332
(1.5)=0.9332
∴ 1-F(85)=1-0.9332=0.0668
∴ 成绩优秀的同学约占6.68%
6、通过本章的学习,要强化理论联系实际,运用数学知识建立实际问题的模型的能力,熟悉运动思想,用有限代替无限的思想。
4、概率密度曲线是某一函数的图象,其中最重要最常见的是正态分布函数。
正态分布函数的解析式: ,x∈(-∞,+∞),其中μ,
,x∈(-∞,+∞),其中μ, (
( >0)分别表示总体的平均数与标准差,可简记为x-N(μ,
>0)分别表示总体的平均数与标准差,可简记为x-N(μ, 2)。此时曲线称为正态曲线:
2)。此时曲线称为正态曲线:
当μ=0, =1时,称为标准正态分布,简记为x-N(0,1),分布密度函数用
=1时,称为标准正态分布,简记为x-N(0,1),分布密度函数用 (x)表示,即
(x)表示,即 ,-∞<x<∞。
,-∞<x<∞。
一般正态分布的问题可以转化为标准正态变量来处理;若ξ-N(μ, 2),作代换
2),作代换 (ξ-μ)/
(ξ-μ)/ ,则ξ-N(0,1)。
,则ξ-N(0,1)。
3、用样本的频率分布估计总体分布,分两种情况:
(1)当总体中的个数体取不同数值很少时,其频率分布表由所取样本的不同数值及其相应的频率来表示,其几何表示就是相应的条形图。例如射击的环数,掷单粒骰子时出现的点数等;
(2)当总体中的个体取不同值较多甚至无限时,此时需要对样本数据进行整理,其频率分布表列出的是在各个不同区间内取值的频率,相应的直方图是用图形面积的大小来表示在各个区间内取值的频率。
画第二种情况频率分布图的步骤是:
①计算最大值与最小值的差;
②决定组距与组数;
③决定分点,通常使分点比数据多一位小数,并且把第一小组的起点稍微减小一点;
④列出频率分布表;
⑤画出频率分布直方图
频率分布将随着样本容量的增大而更加接近总体分布,当样本容量无限增大且分组的组距无限缩小时,频率分布直方图就会演变成一条光滑曲线--反映总体分布的概率密度曲线。正因为频率分布与相应的总体分布的关系,通常是从总体中抽取一个样本,用样本的频率分布去估计相应的总体分布。
2、抽样方法的分类:按照抽取样本时总体中的每个个体被抽取的概率是否相等
本章只研究等概率抽样
等概率抽样
常用的三种抽样方法的比较:
|
类 别 |
共同点 |
不同点 |
联 系 |
适用范围 |
|
简单随 机抽样 |
抽样过程中每个个体被抽取的概率相等 |
从总体中逐个抽取 |
是后两种方法的基础 |
总体个数较少 |
|
系统 抽样 |
将总体均分成几部分,按事先确定的规则在各部分抽取 |
在超始部分抽样时用简单随机抽样 |
总体个数较多 |
|
|
分层 抽样 |
将总体分成几层,分层进行抽取 |
各层抽样时采用简单随机抽样或系统抽样 |
总体由差异明显的几部分组成 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com