
题目列表(包括答案和解析)
2、当a<0时,f(x)在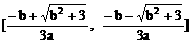 上单调递增;在(-∞,
上单调递增;在(-∞, ,
,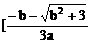 ,+∞)上单调递减。
,+∞)上单调递减。
例6、用总长为14.8m的钢条制作一个长方体容器的框架,如果所制容器的底面的一边比另一边长0.5m,那么为多少时容器的容积最大?并求出它的最大容积?
解题思路分析:
设容器底面短边长为xm,另一边长为(x+0.5)m,高为(3.2-2x)m
∵ 3.2-2x>0,x>0
∴ 0<x<1.6
设容器的容积为ym3
y=x(x+0.5)(3.2-2x)
∴ y=-2x3+2.2x2+1.6x
∴ y’=-6x2+4.4x+1.6
令y’=0得x=1,x=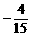 (舍)
(舍)
∵ y在(0,1.6)内只有一个驻点x=1,而x过小或过大时,y值很小
∴ 当x=1时,ymax=1.8,此时高为1.2
例1、 求下列极限
(1)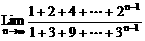 (2)
(2) )
)
解题思路分析:
(1)因分子及分母的次数随n增大而增加,故不能利用运算性质。先求和化简。

∴
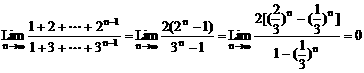
(2)当x→1时,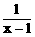 及
及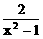 均无意义,应约去因式x-1
均无意义,应约去因式x-1
∵

∴
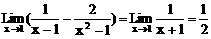
说明:函数 在x=1 无定义,但与
在x=1 无定义,但与 存在无关。一般地有下列结论:如果f(x)=x0处无定义,g(x)在x=x0处有定义并存在极限,且当x≠x0时,f(x)=g(x),则
存在无关。一般地有下列结论:如果f(x)=x0处无定义,g(x)在x=x0处有定义并存在极限,且当x≠x0时,f(x)=g(x),则 。
。
例2、设函数y=ax3+bx2+cx+d的图象与y轴交点为P,且曲线在P点处的切线方程为12x-y-4=0,若函数在x=2处取得极值0,试确定函数的解析式。
解题思路分析:
P(0,d)
∵ 曲线在点P处切线为12x-y-4=0
∴ x=0时,y=d
∴ d=-4
∵ y’=3ax2+2bx+c
∴ y’|x=0=c
又切线斜率k=12
∴ c=12
又函数在x=2处取得极值0
∴
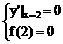
∴
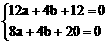
∴

∴ 函数解析式y=2x3-9x2+12x-4
例3、偶函数f(x)=ax4+bx3+cx2+dx+e的图象过点P(0,1),且在x=1处的切线方程为y=x-2
(1)求y=f(x)的解析式;
(2)求y=f(x)的极大(小)值。
解题思路分析:
∵ f(x)是偶函数
∴ b=d=0
又图象过P(0,1)
∴ e=1
此时f(x)=ax4+cx2+1
∵ y’=4ax3+2cx
∴ y’|x=1=4a+2c=1 ①
又切点(1,-1)在曲线上
∴ a+c+1=-1 ②
由①②得: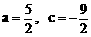
∴
f(x)=
(2)f’(x)=10x3-9x=0
∴
x=0,x=
列表可得: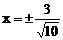 时,f(x)极小=
时,f(x)极小=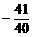
x=0时,f(x)极大=1
例4、曲线 上哪一点的法线在y轴上截距最小?(法线是指过曲线上一点与以此点为切点的切线垂直的直线)
上哪一点的法线在y轴上截距最小?(法线是指过曲线上一点与以此点为切点的切线垂直的直线)
解题思路分析:
在曲线 上任取一点(x0,y0),则过该点切线的斜率为k=2x05
上任取一点(x0,y0),则过该点切线的斜率为k=2x05
∴
法线的斜率为
∴
法线方程y-y0=
令x=0,使法线在y轴上的截距

∴

令y’=0,得x0=±1
当x0<-1时,y’<0,∴y单调递减
当-1<x0<0时,y’>0,∴y单调递增
当0<x0<1时,y’<0,∴y单调减小
当x0>1时,y’>0,则y单递增
∴
当x0=±1时,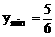 ,此时点(±1,
,此时点(±1,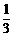 )
)
例5、研究函数f(x)=ax3+bx2-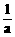 x+1的单调性(a≠0)
x+1的单调性(a≠0)
解题思路分析:
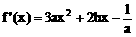
1、a>0时,由f’(x)>0得 或
或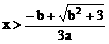
 得
得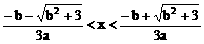
∴
f(x)在(-∞,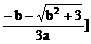 ,
, ,+∞)上单调递增;在
,+∞)上单调递增;在 上单调递减。
上单调递减。
本章主要内容是极限和导数的概念与运算法则,以及导数在几何、函数等方面的应用。
(1)极限是本章也是整个微积分的基础概念,它包括数列极限和函数极限,它们都是是在无限变化过程中(n→∞,x→∞或x→x0)的变化趋势,这一共同点决定了两类极限有类似的运算性质;如果两个数列(或函数)有极限,那么它们的和、差、积、商的极限分别等于这两个数列(或函数)的极限的和、差、积、商(作为除数的数列或函数的极限不能为0)。其原因在于无穷数列{an}是定义域为N+的特殊函数an=f(n),数列的极限 是函数极限
是函数极限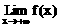 =A的特例。
=A的特例。
极限概念及运算性质决定了确定极限的两种方法:一是利用数形结合思想,从量变中认识质变的数学思想方法,即极限方法。利用极限的方法求出了变速直线运动的瞬时速度与曲线上某点的切线方程,并从中抽象出函数的导数概念。导数是一种特殊的函数极限, ,x0变化时,f’(x0)就是导函数,二是利用极限的运算法则,可推导出最常用的导数公式与运算法则:c’=0(c为常数),(xn)’=nxn-1(n∈N+),[f(x)±g(x)]’=f’(x)±g’(x),[cf(x)]’=cf’(x),进一步可以求出所有多项式函数的导数。
,x0变化时,f’(x0)就是导函数,二是利用极限的运算法则,可推导出最常用的导数公式与运算法则:c’=0(c为常数),(xn)’=nxn-1(n∈N+),[f(x)±g(x)]’=f’(x)±g’(x),[cf(x)]’=cf’(x),进一步可以求出所有多项式函数的导数。
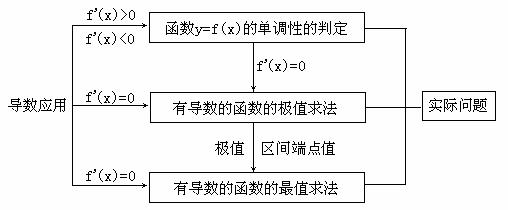 (2)导数f’(x)是函数平均变化率
(2)导数f’(x)是函数平均变化率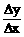 的极限
的极限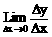 ,瞬时速度、切线斜率、经济学中的边际成本都与平均变化率有关,因而导数有广泛的作用。
,瞬时速度、切线斜率、经济学中的边际成本都与平均变化率有关,因而导数有广泛的作用。
(3)本章思想方法
①极限思想:在变化中求不变,在运动中求静止的思想;
②数形结合思想,如用导数的几何意义及用导数求单调性、极值等。
极限与导数复习
(三) 解答题
20、某天的课程表要排入政治、语文、数学、物理、体育、美术共6节课,如果第1节不排体育,最后1节不排数学,那么共有多少种不同的排课表的方法。
21、有甲、乙、丙三位老师,分到6个班上课:
(1)每人上2个班课,有多少种分法?
(2)甲、乙都上1个班课,丙上4个班课,有多少种分法?
(3)2人各上1个班课,1个人上4个班课,有多少种分法?
22、在x(1-x)k+x2(1+2x)8+x3(1+3x)12的展开式中,含x4的系数是144,求k的值并求出含x2项的系数等于多少?
23、某气象站天气预报的准确率为80%,求:
(1)5次预报中恰有4次准确的概率;
(2)5次预报中至少有4次准确的概率(结果保留2位有效数字)。
24、有6个房间安排4个旅游者住,每人可以进住任一房间,且进住房间是等可能的,试求下列事件的概率:
(1)事件A:指定的4个房间各有1人;
(2)事件B:恰有4个房间中各有1人;
(3)事件C:指定的某个房间中有2人;
(4)事件D:第1号房间有1人,第2号房间有3人。
25、有甲、乙两批种子,发芽率分别为0.8,0.7,从两批种子中各取1粒,求:
(1)2粒种子都能发芽的概率;
(2)至少有1粒种子发芽的概率;
(3)恰好有1粒种子发芽的概率。
26、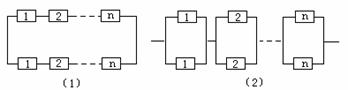 如图构成系统的每个元件的可靠性为r(0<r,r<1),且各个元件能否正常工作是相互独立的,试求图中两种系统的可靠性。
如图构成系统的每个元件的可靠性为r(0<r,r<1),且各个元件能否正常工作是相互独立的,试求图中两种系统的可靠性。
(二) 填空题
15、空间12个点,其中5个点共面,此外无任何4个点共面,这12个点最多可决定_________个不同的平面。
16、(4+2x+x2)(2-x)7展开式中x5的系数为________。
17、 =__________。
=__________。
18、有1个数字难题,在半小时内,甲能解决它的概率是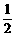 ,乙能解决它的概率是
,乙能解决它的概率是 ,两人试图独立地在半小时内解决它,则:两人都未解决的概率为__________;问题得到解决的概率为__________。
,两人试图独立地在半小时内解决它,则:两人都未解决的概率为__________;问题得到解决的概率为__________。
19、一次考试出了10个选择题,每道题有4个可供选择的答案,其中1个是正确的,3个是错误的,某学生只知道5个题的正确答案,对其他5个题全靠猜回答,那么这个学生卷面上正确答案不少于7个题的概率是_________。
(一) 选择题
1、某一排共12个座位,现甲、乙、丙三人按如下要求入座,每人左右两旁都有空座位,且三人的顺序是甲必须在另两人之间,则不同的座法共有
A、60种 B、112种 C、242种 D、672种
2、某同学从6门课中选学2门,其中有2门课上课时间有冲突,另有2门不允许同时选学,则该同学可选学的方法总数有
A、8种 B、13种 C、12种 D、9种
3、 如图,在某城市中,M、N两地间有整齐的道路网,若规定只能向东或向北两个方向沿图中的矩形的边前进,则从M到N不同的走法共有
如图,在某城市中,M、N两地间有整齐的道路网,若规定只能向东或向北两个方向沿图中的矩形的边前进,则从M到N不同的走法共有
A、13种 B、15种 C、25种 D、10种
4、将n个不同的小球放入n个不同的盒子里,恰好有一个空盒的放法种数是
A、 B、
B、 C、
C、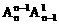 D、
D、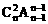
5、若(1-2x)9=a0+a1x+a2x2+…+a8x8+a9x9,则a1+a2+…+a8的值为
A、-1 B、-2 C、-512 D、510
6、 展开式中,x4的系数为
展开式中,x4的系数为
A、-40 B、10 C、40 D、45
7、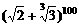 的展开式中无理项的个数是
的展开式中无理项的个数是
A、84 B、85 C、86 D、87
8、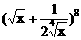 的展开式中系数最大的项是
的展开式中系数最大的项是
A、第3项 B、第4项 C、第2或第3项 D、第3或第4项
9、掷三颗骰子(各面上分别标以数字1到6的均匀正方体玩具),恰有一颗骰子出1点或6点的概率是
A、 B、
B、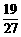 C、
C、 D、
D、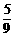
10、一工人看管三台机床,在一小时内甲、乙、丙三台机床需要工人照看的概率分别是0.9,0.8和0.85,那么在一小时中至少有一台机床不需要照看的概率是
A、0.003 B、0.612 C、0.388 D、0.027
11、在4次独立重复试验中,随机事件A恰好发生1次的概率不大于其恰好发生两次的概率,则事件A在一次试验中发生的概率P的取值范围是
A、[0.4,1] B、(0,0.4] C、(0,0.6] D、[0.6,1)
12、一批零件10个,其中有8个合格品,2个次品,每次任取一个零件装配机器,若第一次取得合格品的概率是P1,第二次取得合格品的概率是P2,则
A、P1>P2 B、P1=P2 C、P1<P2 D、P1=2P2
13、一个学生通过某种英语听力测试的概率是1/2,他连续测试n次,要保证他至少有一次通过的概率大于0.9,那么n的最小值为
A、3 B、4 C、5 D、6
14、甲、乙两人投篮命中的概率分别为p、q,他们各投两次,若p=1/2,且甲比乙投中次数多的概率恰好等于7/36,则q的值为
A、 B、
B、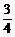 C、
C、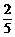 D、
D、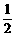
例1、用n种不同颜色为下列两块广告牌着色(如图),要求在①,②,③,④个区域中相邻(有公共边界)的区域不用同一种颜色。
(1)若n=6,为甲着色时共有多少种不同方法?
(2)若为乙着色时共有120种不同方法,求n。
解:完成着色这件事,共分四个步骤,可依次考虑为①、②、③、④着色时各自的方法数,再由乘法原理确定决的着色方法数。因此
(1)为①着色有6种方法,为②着色有5种方法,为③着色有4种方法,为④着色也只有4种方法。
∴ 共有着色方法6×5×4×4=480种
 (2)与①的区别在于与④相邻的区域由两块变成了三块,同理,不同的着色方法数是n(n-1)(n-2)(n-3)
(2)与①的区别在于与④相邻的区域由两块变成了三块,同理,不同的着色方法数是n(n-1)(n-2)(n-3)
由n(n-1)(n-2)(n-3)=120
∴ (n2-3n)(n2-3n+2)-120=0
即(n2-3n)2+2(n2-3n)-12×10=0
∴ n2-3n-10=0
∴ n=5
例2、计算下列各题:
(1)
(2)
(3)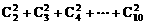
解:(1)原式=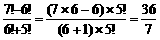
(2)原式=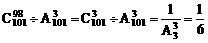
(3)原式=
=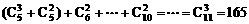
例3、按以下要求分配6本不同的书,各有几种分法?
(1)平均分给甲、乙、丙三人,每人2本;
(2)平均分成三份,每份2本;
(3)甲、乙、丙三人一人得1本,一人得2本,一人得3本;
(4)分成三份,一份1本,一份2本,一份3本;
(5)甲、乙、丙三人中,一人得4本,另二人每人得1本;
(6)分成三份,一份4本,另两份每份1本;
(7)甲得1本,乙得1本,丙得4本(均只要求列式)
解:(1) ;
;
(2)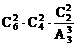
(3)
(4)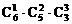
(5)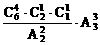
(6)
(7)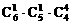
评注:有关排列组合混合题常常是先组合再排列。
例4、四面体的顶点和各棱中点共有10个点,在其中取4个不共面的点,不同的取法共有( )
A、150种 B、147种 C、144种 D、141种
解:从10个点中任取4个点有 种取法,其中4点共面的情况有三类。第一类,取出的4个点位于四面体的同一个面内,有
种取法,其中4点共面的情况有三类。第一类,取出的4个点位于四面体的同一个面内,有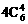 种;第二类,取任一条棱上的3个点及该棱对棱的中点,这4点共面,有6种;第三类,由中位线构成的平行四边形(其两组对边分别平行于四面体相对的两条棱),它的4个点共面,有3种。以上三种情况不合要求应减掉,所以不同的取法共有
种;第二类,取任一条棱上的3个点及该棱对棱的中点,这4点共面,有6种;第三类,由中位线构成的平行四边形(其两组对边分别平行于四面体相对的两条棱),它的4个点共面,有3种。以上三种情况不合要求应减掉,所以不同的取法共有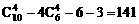 (种)
(种)
例5、求(4+2x+x2)(2-x)7的展开式中x5的系数。
解:(4+2x+x2)(2-x)7=(8-x3)(x-2)6
=(8-x3)[(x6-2C61x5+(-2)2C62x4+(-2)3C63x3+(-2)4C64x2+…]
∴ 含x5的项为-2×8×C61·x5-(-2)4C64x5=-336x5
∴ x5的系数为-336
例6、已知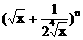 的展开式前三项中的x的系数成等差数列。
的展开式前三项中的x的系数成等差数列。
(1)求展开式里所有的x的有理项;
(2)求展开式里系数最大的项。
解:(1)∵ 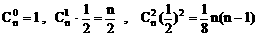
由题设可知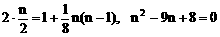
解得n=8或n=1(舍去)
当n=8时,通项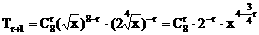
据题意, 必为整数,从而可知r必为4的倍数,而0≤r≤8
必为整数,从而可知r必为4的倍数,而0≤r≤8
∴
r=0,4,8,故x的有理项为 ,
, ,
,
(3)设第r+1项的系数tr+1最大,显然tr+1>0,故有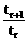 ≥1且
≥1且 ≤1
≤1
∵
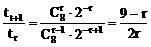
由 ≥1得r≤3
≥1得r≤3
又∵
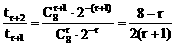
由 ≤1得:r≥2
≤1得:r≥2
∴
r=2或r=3所求项为 和
和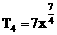
例7、设a>1,n∈N,且n≥2,求证: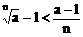
证明:设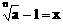 ,则(x+1)n=a
,则(x+1)n=a
欲证原不等式,即证nx<(x+1)n-1,其中x>0
∵
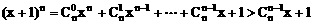
即(x+1)n>nx+1,原不等式成立。
评注:由于(a+b)n的展开式共有n+1项,故可通过对某些项的取舍来达到近似计算或证明不等式的目的。
例8、盒中有6只灯泡,其中2只次品,4只正品,有放回地从中任取两次,每次取一只,试求下列事件的概率:
(1)取到的2只都是次品;
(2)取到的2只中正品、次品各一只;
(3)取到的2只中至少有一只正品。
解:从6只灯泡中有放回地任取两只,共有62=36种不同取法
(1)取到的2只都是次品情况为22=4种,因而所求概率为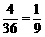
(2)由于取到的2只中正品、次品各一只有两种可能:第一次取到正品,第二次取到次品;及第一次取到次品,第二次取到正品。因而所求概率为
(3)由于“取到的两只中至少有一只正品”是事件“取到的两只都是次品”的对立事件,因而所求概率为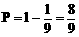
例9、甲、乙两人独立地破译1个密码,他们能译出的密码的概率分别为 和
和 ,求:
,求:
(1)恰有1人译出的密码的概率;
(2)至多1人译出的密码的概率;
(3)若达到译出的密码的概率为 ,至少需要多少个乙这样的人。
,至少需要多少个乙这样的人。
解:记“甲译出密码”为事件A,“甲译不出密码”这事件 ;记“乙译出密码”为事件B,“乙译不出密码”为事件
;记“乙译出密码”为事件B,“乙译不出密码”为事件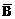 ;“两人都译出密码”为事件C,“两人都译不出密码”为事件D;“恰有1人译出密码”为事件E;“至多1人译出密码”为事件F。
;“两人都译出密码”为事件C,“两人都译不出密码”为事件D;“恰有1人译出密码”为事件E;“至多1人译出密码”为事件F。
(1)“恰有1人译出密码”是包括2种情况:一种是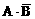 ,另一种是
,另一种是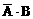 。这两种情况不能同时发生,是互斥的。
。这两种情况不能同时发生,是互斥的。
∴
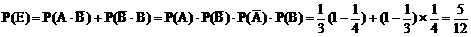
(2)“至多1人译出密码”包括两种情况:“2人都译不出密码”或“恰有1人译出密码”,即事件D+E,且事件D、E是互斥的
∴

(3)n个乙这样的人都译不出密码的概率为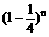 ,根据题意得:
,根据题意得: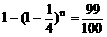
解得:n=16
例10、某数学家有两盒火柴,每盒都有n根火柴,每次用火柴时他在两盒中任取一盒并从中抽出一根,求他发现用完一盒时另一盒还有r根(1≤r≤n)的概率。
解析:由题意知:数学家共用了2n-r根火柴,其中n根取自一盒火柴,n-r根取自另一盒火柴。
由于数学家取火柴时,每次他在两盒中任取一盒并从中抽取一根,故他用完的那一盒取出火柴的概率是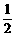 ,他不从此盒中取出一根火柴的概率也是
,他不从此盒中取出一根火柴的概率也是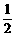 。
。
由于所取的2n-r根火柴,有n根取自用完的那一盒的概率为:
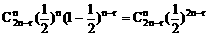
5、概率
(1)概率是频率的近似值,两者是不同概念
(2)等可能事件中概率 ,P(A)∈[0,1]
,P(A)∈[0,1]
(3)互斥事件A,B中有一个发生的概率:加法公式P(A+B)=P(A)+P(B)
特例: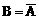 时,
时,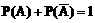 ,即对立事件的概率和为1
,即对立事件的概率和为1
(4)相互独立事件A,B同时发生的概率P(A·B)=P(A)P(B)
(5)事件A在n次独立重复试验中恰好发生k次的概率Pn(k)=CnkPk(1-P)n-k,其中P为事件A在一次试验中发生的概率,此式为二项式[(1-P)+P]n展开的第k+1项
4、二项式定理

通项公式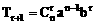 ,r=0,1,2,…,n
,r=0,1,2,…,n
二项式系数的性质:
(1)对称性,在展开式中,与首末两端“等距离”的两个二项式系数相等,即 ,
,
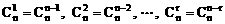 ;
;
(2)增减性与最大值:在二项式展开式中,二项式系数先增后减,且在中间取得最大值,当n是偶数时,中间一项 最大;当n是奇数时,中间两项
最大;当n是奇数时,中间两项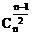 ,
,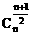 相等,且为最大值;
相等,且为最大值;
(3)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com