
题目列表(包括答案和解析)
4、本单常见的初等函数;一次函数,二次函数,反比例函数,指数函数,对数函数。在具体的对应法则下理解函数的通性,掌握这些具体对应法则的性质。分段函数是重要的函数模型。
对于抽象函数,通常是抓住函数特性是定义域上恒等式,利用赋值法(变量代换法)解题。联系到具体的函数模型可以简便地找到解题思路,及解题突破口。
应用题是函数性质运用的重要题型。审清题意,找准数量关系,把握好模型是解应用题的关键。
3、函数的图象
函数的图象既是函数性质的一个重要方面,又能直观地反映函数的性质,在解题过程中,充分发挥图象的工具作用。
图象作法:①描点法;②图象变换。应掌握常见的图象变换。
2、函数的通性
(1)奇偶性:函数定义域关于原点对称是判断函数奇偶性的必要条件,在利用定义判断时,应在化简解析式后进行,同时灵活运用定义域的变形,如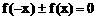 ,
,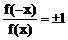 (f(x)≠0)。
(f(x)≠0)。
奇偶性的几何意义是两种特殊的图象对称。
函数的奇偶性是定义域上的普遍性质,定义式是定义域上的恒等式。
利用奇偶性的运算性质可以简化判断奇偶性的步骤。
(2)单调性:研究函数的单调性应结合函数单调区间,单调区间应是定义域的子集。
判断函数单调性的方法:①定义法,即比差法;②图象法;③单调性的运算性质(实质上是不等式性质);④复合函数单调性判断法则。
函数单调性是单调区间上普遍成立的性质,是单调区间上恒成立的不等式。
函数单调性是函数性质中最活跃的性质,它的运用主要体现在不等式方面,如比较大小,解抽象函数不等式等。
(3)周期性:周期性主要运用在三角函数及抽象函数中,是化归思想的重要手段。
求周期的重要方法:①定义法;②公式法;③图象法;④利用重要结论:若函数f(x)满足f(a-x)=f(a+x),f(b-x)=f(b+x),a≠b,则T=2|a-b|。
(4)反函数:函数是否是有反函数是函数概念的重要运用之一,在求反函数之前首先要判断函数是否具备反函数,函数f(x)的反函数f-1(x)的性质与f(x)性质紧密相连,如定义域、值域互换,具有相同的单调性等,把反函数f-1(x)的问题化归为函数f(x)的问题是处理反函数问题的重要思想。
设函数f(x)定义域为A,值域为C,则
f-1[f(x)]=x,x∈A
f[f-1(x)]=x,x∈C
1、函数的概念:
(1)映射:设非空数集A,B,若对集合A中任一元素a,在集合B中有唯一元素b与之对应,则称从A到B的对应为映射,记为f:A→B,f表示对应法则,b=f(a)。若A中不同元素的象也不同,则称映射为单射,若B中每一个元素都有原象与之对应,则称映射为满射。既是单射又是满射的映射称为一一映射。
(2)函数定义:函数就是定义在非空数集A,B上的映射,此时称数集A为定义域,象集C={f(x)|x∈A}为值域。定义域,对应法则,值域构成了函数的三要素,从逻辑上讲,定义域,对应法则决定了值域,是两个最基本的因素。逆过来,值域也会限制定义域。
求函数定义域,通过解关于自变量的不等式(组)来实现的。要熟记基本初等函数的定义域,通过四则运算构成的初等函数,其定义域是每个初等函数定义域的交集。复合函数定义域,不仅要考虑内函数的定义域,还要考虑到外函数对应法则的要求。理解函数定义域,应紧密联系对应法则。函数定义域是研究函数性质的基础和前提。
函数对应法则通常表现为表格,解析式和图象。其中解析式是最常见的表现形式。求已知类型函数解析式的方法是待定系数法,抽象函数的解析式常用换元法及凑合法。
求函数值域是函数中常见问题,在初等数学范围内,直接法的途径有单调性,基本不等式及几何意义,间接法的途径为函数与方程的思想,表现为△法,反函数法等,在高等数学范围内,用导数法求某些函数最值(极值)更加方便。
在中学数学的各个部分都存在着求取值范围这一典型问题,它的一种典型处理方法就是建立函数解析式,借助于求函数值域的方法。
2、函数性质的运用。
1、函数的定义及通性;
《函数》单元复习
(三) 解答题
17、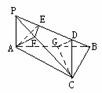 如图,在斜边为AB的直角三角形ABC中,过A作AP⊥平面ABC,AE⊥PB于E,AF⊥PC于F,CG⊥AB于G,CD⊥PB于D。
如图,在斜边为AB的直角三角形ABC中,过A作AP⊥平面ABC,AE⊥PB于E,AF⊥PC于F,CG⊥AB于G,CD⊥PB于D。
(1)求证∠AEF=∠CDG;(2)求△AEF面积的最大值。
18、等边三角形ABC的边长为a,沿平行BC的线段PQ折起,使平面APQ⊥平面PBCQ,设点A到直线PQ的距离为x,AB的长为d
(1)x为何值时,d2取得最小值,最小值是多少?(2)若∠BAC=θ,求cosθ的最小值。
19、 如图,ABCD是矩形,其4个顶点在平面α的同一侧,且它们在平面α内的射影分别为A’,B’,C’,D’,直线A’B与C’D’不重合,
如图,ABCD是矩形,其4个顶点在平面α的同一侧,且它们在平面α内的射影分别为A’,B’,C’,D’,直线A’B与C’D’不重合,
(1)求证:A’B’C’D’是平行四边形;
(2)在怎样的条件下,A’B’C’D’是矩形?并证明你的结论。
20、正三棱锥V-ABC的底面边长为a,侧棱与底面所成的角等于θ(θ>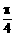 ),过底面一边作此棱锥的截面,当截面与底面所成二面角为何值时,截面面积最小?并求出最小值。
),过底面一边作此棱锥的截面,当截面与底面所成二面角为何值时,截面面积最小?并求出最小值。
(二) 填空题
13、已知异面直线a与b所成的角是500,空间有一定点P,则过点P与a,b所成的角都是300的直线有________条。
14、线段AB的端点到平面α的距离分别为6cm和2cm,AB在α上的射影A’B’的长为3cm,则线段AB的长为
__________。
15、正n棱锥相邻两个侧面所成二面角的取值范围是____________。
16、如果一个简单多面体的每个面都是奇数的多边形,那么它的面数是__________。
(一) 选择题
1、1∥2,a,b与1,2都垂直,则a,b的关系是
A、平行 B、相交 C、异面 D、平行、相交、异面都有可能
2、异面直线a,b,a⊥b,c与a成300,则c与b成角范围是
A、[600,900] B、[300,900] C、[600,1200] D、[300,1200]
3、正方体AC1中,E、F分别是AB、BB1的中点,则A1E与C1F所成的角的余弦值是
A、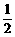 B、
B、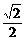 C、
C、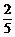 D、
D、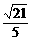
4、在正△ABC中,AD⊥BC于D,沿AD折成二面角B-AD-C后,BC=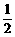 AB,这时二面角B-AD-C大小为
AB,这时二面角B-AD-C大小为
A、600 B、900 C、450 D、1200
5、一个山坡面与水平面成600的二面角,坡脚的水平线(即二面角的棱)为AB,甲沿山坡自P朝垂直于AB的方向走30m,同时乙沿水平面自Q朝垂直于AB的方向走30m,P、Q都是AB上的点,若PQ=10m,这时甲、乙2个人之间的距离为
A、 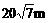 B、
B、 C、
C、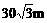 D、
D、
6、E、F分别是正方形ABCD的边AB和CD的中点,EF交BD于O,以EF为棱将正方形折成直二面角如图,则∠BOD=
A、1350 B、1200 C、1500 D、900
7、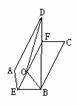 三棱锥V-ABC中,VA=BC,VB=AC,VC=AB,侧面与底面ABC所成的二面角分别为α,β,γ(都是锐角),则cosα+cosβ+cosγ等于
三棱锥V-ABC中,VA=BC,VB=AC,VC=AB,侧面与底面ABC所成的二面角分别为α,β,γ(都是锐角),则cosα+cosβ+cosγ等于
A、1
B、2 C、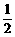 D、
D、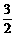
8、正n棱锥侧棱与底面所成的角为α,侧面与底面所成的角为β,tanα∶tanβ等于
A、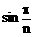 B、
B、 C、
C、 D、
D、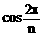
9、一个简单多面体的各面都是三角形,且有6个顶点,则这个简单多面体的面数是
A、4 B、6 C、8 D、10
10、三棱锥P-ABC中,3条侧棱两两垂直,PA=a,PB=b,PC=c,△ABC的面积为S,则P到平面ABC的距离为
A、 B、
B、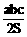 C、
C、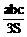 D、
D、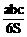
11、三棱柱ABC-A1B1C1的体积为V,P、Q分别为AA1、CC1上的点,且满足AP=C1Q,则四棱锥B-APQC的体积是
A、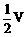 B、
B、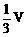 C、
C、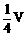 D、
D、
12、多面体ABCDEF中,已知面ABCD是边长为3的正方形,EF∥AB,EF=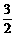 ,EF与面AC的距离为2,则该多面体的体积为
,EF与面AC的距离为2,则该多面体的体积为
A、 B、5 C、6
D、
B、5 C、6
D、
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com