1、上一章已经复习过解析几何的基本问题之一：如何求曲线(点的轨迹)方程。它一般分为两类基本题型：一是已知轨迹类型求其方程，常用待定系数法，如求直线及圆的方程就是典型例题；二是未知轨迹类型，此时除了用代入法、交轨法、参数法等求轨迹的方法外，通常设法利用已知轨迹的定义解题，化归为求已知轨迹类型的轨迹方程。因此在求动点轨迹方程的过程中，一是寻找与动点坐标有关的方程(等量关系)，侧重于数的运算，一是寻找与动点有关的几何条件，侧重于形，重视图形几何性质的运用。

在基本轨迹中，除了直线、圆外，还有三种圆锥曲线：椭圆、双曲线、抛物线。

2、三种圆锥曲线的研究

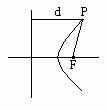
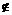　 (1)统一定义，三种圆锥曲线均可看成是这样的点集：，其中F为定点，d为P到定直线的距离，F，如图。

因为三者有统一定义，所以，它们的一些性质，研究它们的一些方法都具有规律性。

当0<e<1时，点P轨迹是椭圆；当e>1时，点P轨迹是双曲线；当e=1时，点P轨迹是抛物线。

　 (2)椭圆及双曲线几何定义：椭圆：{P||PF₁|+|PF₂|=2a，2a>|F₁F₂|>0，F₁、F₂为定点}，双曲线{P|||PF₁|-|PF₂||=2a，|F₁F₂|>2a>0，F₁，F₂为定点}。

　 (3)圆锥曲线的几何性质：几何性质是圆锥曲线内在的，固有的性质，不因为位置的改变而改变。

①定性：焦点在与准线垂直的对称轴上

椭圆及双曲线中：中心为两焦点中点，两准线关于中心对称；椭圆及双曲线关于长轴、短轴或实轴、虚轴成轴对称，关于中心成中心对称。

②定量：

	椭　　 圆	双 曲 线	抛 物 线
焦　 距	2c
长轴长	2a	--
实轴长	--	2a
短轴长	2b
焦点到对应 准线距离	P=2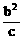	p
通径长	2·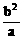	2p
离心率		1
基本量关系	a2=b2+c2	C2=a2+b2

　 (4)圆锥曲线的标准方程及解析量(随坐标改变而变)

举焦点在x轴上的方程如下：

	椭　　 圆	双 曲 线	抛 物 线
标准方程	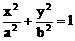(a>b>0)	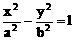(a>0，b>0)	y2=2px(p>0)
顶　 点	(±a，0) (0，±b)	(±a，0)	(0，0)
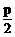焦　 点	(±c，0)	(，0)
准　 线	X=±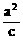	x=
中　 心	(0，0)
有界性	|x|≤a |y|≤b	|x|≥a	x≥0
焦半径	P(x0，y0)为圆锥曲线上一点，F1、F2分别为左、右焦点
|PF1|=a+ex0 　|PF2|=a-ex0	P在右支时： 　|PF1|=a+ex0 　 |PF2|=-a+ex0 P在左支时： 　|PF1|=-a-ex0 　 |PF2|=a-ex0	|PF|=x0+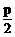

总之研究圆锥曲线，一要重视定义，这是学好圆锥曲线最重要的思想方法，二要数形结合，既熟练掌握方程组理论，又关注图形的几何性质，以简化运算。

3、求轨迹方程的常规方法。

2、直线和圆锥曲线位置关系。

1、三种圆锥曲线：椭圆、双曲线、抛物线的定义、标准方程、几何性质等。

《圆锥曲线方程》复习

(三)　　　 解答题

16、若函数 的值域为[-1，5]，求a，c。

　　 17、设定义在[-2，2]上的偶函数f(x)在区间[0，2]上单调递减，若f(1-m)<f(m)，求实数m的取值范围。

18、已知0<a<1，在函数y=log_ax(x≥1)的图象上有A，B，C三点，它们的横坐标分别是t，t+2，t+4

(1)　　　　　 若△ABC面积为S，求S=f(t)；

(2)　　　　　 判断S=f(t)的单调性；

(3)　　　　　 求S=f(t)最大值。

19、设f(x)=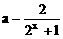，x∈R

(1)　　　　　 证明：对任意实数a，f(x)在(-∞，+∞)上是增函数；

(2)　　　　　 当f(x)为奇函数时，求a；

(3)　　　　　 当f(x)为奇函数时，对于给定的正实数k，解不等式。

20、设0<a<1，函数f(x)=的定义域为[m，n]，值[log_aa(n-1)，log_aa(m-1)]，　　　

(1)　　　　　 求证：m>3；

(二)　　　 填空题

　　 7、已知定义在R的奇函数f(x)满足f(x+2)=-f(x)，且当0≤x≤1时，f(x)=x，则=__________。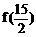

8、　 已知y=log_a(2-x)是x的增函数，则a的取值范围是__________。

9、　 函数f(x)定义域为[1，3]，则f(x²+1)的定义域是__________。

　　 10、函数f(x)=x²-bx+c满足f(1+x)=f(1-x)，且f(0)=3，则f(b^x)与f(c^x)的大小关系是__________。

　　 11、已知f(x)=log₃x+3，x∈[1，9]，则y=[f(x)]²+f(x²)的最大值是__________。

12、已知A={y|y=x²-4x+6，y∈N}，B={y|y=-x²-2x+18，y∈N}，则A∩B中所有元素的和是__________。

13、若φ(x)，g(x)都是奇函数，f(x)=mφ(x)+ng(x)+2在(0，+∞)上有最大值，则f(x)在(-∞，0)上最小值

为__________。

14、函数y=log₂(x²+1)(x>0)的反函数是__________。

15、求值：=__________。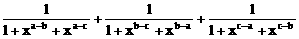

(一)　　　 选择题

　　 1、定义在R上的偶函数f(x)满足f(x+1)=-f(x)，且在[-1，0]上单调递增，设a=f(3)，b=f()，c=f(2)，则a，b，c大小关系是

A、a>b>c　　　　 　　　　 B、a>c>b　　　　 　　　　 C、b>c>a　　　　 　　　　 D、c>b>a

2、方程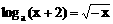(a>0且a≠1)的实数解的个数是

A、0　　　　　　 　　　　 B、1 　　　　　　　　　 C、2　　　　　　 　　　　 D、3

3、的单调减区间是

A、(-∞，1)　　 　　　　 B、(1，+∞)　　 　　　　 C、(-∞，-1)∪(1，+∞) D、(-∞，+∞)

4、函数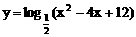的值域为

A、　 (-∞，3]　　　 　　　 B、(-∞，-3]　　　 　　　 C、(-3，+∞)　　　 　　 D、(3，+∞)

5、函数y=log₂|ax-1|(a≠b)的图象的对称轴是直线x=2，则a等于

A、　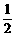 　　　　　　　　　 B、　　　　　 　　　 C、2　　　　　　　 　　 D、-2

　　 6、有长度为24的材料用一矩形场地，中间加两隔墙，要使矩形的面积最大，则隔壁的长度为

A、　 3　　　　　　　 　　　 B、4 　　　　　　　　　 C、6　　　　　　　 　　 D、12

　　 例1、已知，函数y=g(x)图象与y=f^-1(x+1)的图象关于直线y=x对称，求g(11)的值。

解题思路分析：

利用数形对应的关系，可知y=g(x)是y=f^-1(x+1)的反函数，从而化g(x)问题为已知f(x)。

∵ y=f^-1(x+1)

∴ x+1=f(y)

∴ x=f(y)-1

∴ y=f^-1(x+1)的反函数为y=f(x)-1

即 g(x)=f(x)-1

∴ g(11)=f(11)-1=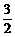

评注：函数与反函数的关系是互为逆运算的关系，当f(x)存在反函数时，若b=f(a)，则a=f^-1(b)。

例2、设f(x)是定义在(-∞，+∞)上的函数，对一切x∈R均有f(x)+f(x+2)=0，当-1<x≤1时，f(x)=2x-1，求当1<x≤3时，函数f(x)的解析式。

解题思路分析：

利用化归思想解题

∵ f(x)+f(x+2)=0

∴ f(x)=-f(x+2)

∵ 该式对一切x∈R成立

∴ 以x-2代x得：f(x-2)=-f[(x-2)+2]=-f(x)

当1<x≤3时，-1<x-2≤1

∴ f(x-2)=2(x-2)-1=2x-5

∴ f(x)=-f(x-2)=-2x+5

∴ f(x)=-2x+5(1<x≤3)

评注：在化归过程中，一方面要转化自变量到已知解析式的定义域，另一方面要保持对应的函数值有一定关系。在化归过程中还体现了整体思想。

例3、已知g(x)=-x²-3，f(x)是二次函数，当x∈[-1，2]时，f(x) 的最小值，且f(x)+g(x)为奇函数，求f(x)解析式。

解题思路分析：

用待定系数法求f(x)解析式

设f(x)=ax²+bx+c(a≠0)

则f(x)+g(x)=(a-1)x²+bx+c-3

由已知f(x)+g(x)为奇函数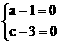

∴

∴ f(x)=x²+bx+3

下面通过确定f(x)在[-1，2]上何时取最小值来确定b，分类讨论。

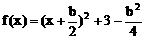　 ，对称轴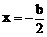

(1)　　　　　 当≥2，b≤-4时，f(x)在[-1，2]上为减函数

∴

∴ 2b+7=1

∴ b=3(舍)

(2)　　　　　 当(-1，2)，-4<b<2时

∴

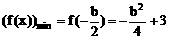
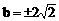∴ (舍负)

(3)　　　　　 当≤-1，b≥2时，f(x)在[-1，2]上为增函数

　∴ (f(x)_min=f(1)=4-b

　∴ 4-b=1

　∴ b=3

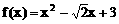　∴ ，或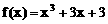

评注：二次函数在闭区间上的最值通常对对称轴与区间的位置关系进行讨论，是求值域的基本题型之一。在已知最值结果的条件下，仍需讨论何时取得最小值。

例4、定义在R上的函数y=f(x)，f(0)≠0，当x>0时，f(x)>1，且对任意的a、b∈R，有f(a+b)=f(a)f(b)，

(1)　　　　　 求证：f(0)=1；

(2)　　　　　 求证：对任意的x∈R，恒有f(x)>0；

(3)　　　　　 证明：f(x)是R上的增函数；

(4)　　　　　 若f(x)·f(2x-x²)>1，求x的取值范围。

　解题思路分析：

(1)　　　　　 令a=b=0，则f(0)=[f(0)]²

　∵ f(0)≠0

　∴ f(0)=1

(2)　　　　　 令a=x，b=-x

　则 f(0)=f(x)f(-x)

　∴

　由已知x>0时，f(x)>1>0

　当x<0时，-x>0，f(-x)>0

　∴

　又x=0时，f(0)=1>0

　∴ 对任意x∈R，f(x)>0

(3)　　　　　 任取x₂>x₁，则f(x₂)>0，f(x₁)>0，x₂-x₁>0

　∴

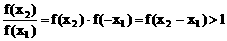
　∴ f(x₂)>f(x₁)

　∴ f(x)在R上是增函数

(4)　　　　　 f(x)·f(2x-x²)=f[x+(2x-x²)]=f(-x²+3x)

　又1=f(0)，f(x)在R上递增

　∴ 由f(3x-x²)>f(0)得：3x-x²>0

　∴ 0<x<3

评注：根据f(a+b)=f(a)·f(b)是恒等式的特点，对a、b适当赋值。利用单调性的性质去掉符号“f”得到关于x的代数不等式，是处理抽象函数不等式的典型方法。

例5、已知lgx+lgy=2lg(x-2y)，求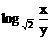的值。

解题思路分析：

在化对数式为代数式过程中，全面挖掘x、y满足的条件

由已知得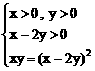

∴ x=4y，

∴

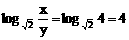
例6、某工厂今年1月，2月，3月生产某产品分别为1万件，1.2万件，1.3万件，为了估测以后每个月的产量，以这三个月的产品数量为依据，用一个函数模拟该产品的月产量y与月份数x的关系，模拟函数可选用y=ab^x+c(其中a，b，c为常数)或二次函数，已知4月份该产品的产量为1.37万件，请问用哪个函数作为模拟函数较好？并说明理由。

解题思路分析：

设f(x)=px²+qx+r(p≠0)

则

∴

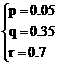
∴ f(4)=-0.05×4²+0.35×4+0.7=1.3

设g(x)=ab^x+c

则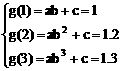

∴

∴ g(4)=-0.8×0.5⁴+1.4=1.35

∵ |1.35-1.37|<|1.3-1.37|

∴ 选用y=-0.8×(0.5)^x+1.4作为模拟函数较好。

5、主要思想方法：数形结合，分类讨论，函数方程，化归等。