
题目列表(包括答案和解析)
8. 讨论不等式的解
求解这类问题利用函数的单调性进行转化,脱去函数符号。
例12. 已知函数 是定义在
是定义在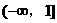 上的减函数,且对一切实数x,不等式
上的减函数,且对一切实数x,不等式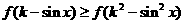 恒成立,求k的值。
恒成立,求k的值。
分析:由单调性,脱去函数记号,得
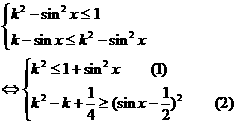
由题意知(1)(2)两式对一切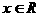 恒成立,则有
恒成立,则有
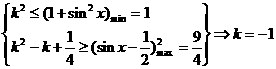
7. 讨论方程根的问题
例11. 已知函数 对一切实数x都满足
对一切实数x都满足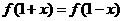 ,并且
,并且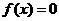 有三个实根,则这三个实根之和是_______。
有三个实根,则这三个实根之和是_______。
分析:由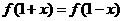 知直线
知直线 是函数
是函数 图象的对称轴。
图象的对称轴。
又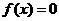 有三个实根,由对称性知
有三个实根,由对称性知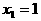 必是方程的一个根,其余两根
必是方程的一个根,其余两根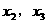 关于直线
关于直线 对称,所以
对称,所以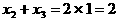 ,故
,故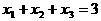 。
。
6. 比较函数值大小
利用函数的奇偶性、对称性等性质将自变量转化到函数的单调区间内,然后利用其单调性使问题获解。
例10. 已知函数 是定义域为R的偶函数,
是定义域为R的偶函数,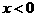 时,
时, 是增函数,若
是增函数,若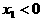 ,
,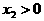 ,且
,且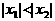 ,则
,则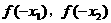 的大小关系是_______。
的大小关系是_______。
分析: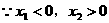 且
且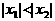 ,
,
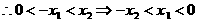
又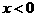 时,
时, 是增函数,
是增函数,
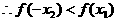
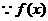 是偶函数,
是偶函数,
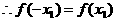
故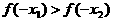
5. 求函数值
紧扣已知条件进行迭代变换,经有限次迭代可直接求出结果,或者在迭代过程中发现函数具有周期性,利用周期性使问题巧妙获解。
例8. 已知 的定义域为
的定义域为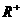 ,且
,且 对一切正实数x,y都成立,若
对一切正实数x,y都成立,若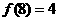 ,则
,则 _______。
_______。
分析:在条件 中,令
中,令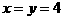 ,得
,得
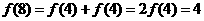 ,
,
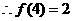
又令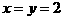 ,
,
得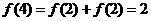 ,
,
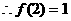
例9. 已知 是定义在R上的函数,且满足:
是定义在R上的函数,且满足: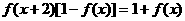 ,
,
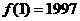 ,求
,求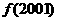 的值。
的值。
分析:紧扣已知条件,并多次使用,发现 是周期函数,显然
是周期函数,显然 ,于是
,于是
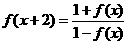 ,
,
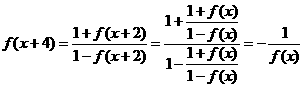
所以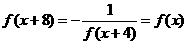
故 是以8为周期的周期函数,从而
是以8为周期的周期函数,从而
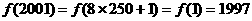
4. 探求周期性
这类问题较抽象,一般解法是仔细分析题设条件,通过类似,联想出函数原型,通过对函数原型的分析或赋值迭代,获得问题的解。
例7. 设函数 的定义域为R,且对任意的x,y有
的定义域为R,且对任意的x,y有
 ,并存在正实数c,使
,并存在正实数c,使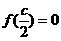 。试问
。试问 是否为周期函数?若是,求出它的一个周期;若不是,请说明理由。
是否为周期函数?若是,求出它的一个周期;若不是,请说明理由。
分析:仔细观察分析条件,联想三角公式,就会发现: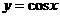 满足题设条件,且
满足题设条件,且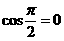 ,猜测
,猜测 是以2c为周期的周期函数。
是以2c为周期的周期函数。
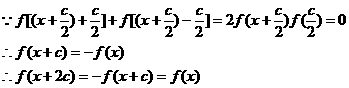
故 是周期函数,2c是它的一个周期。
是周期函数,2c是它的一个周期。
3. 判断单调性
根据函数的奇偶性、单调性等有关性质,画出函数的示意图,以形助数,问题迅速获解。
例5. 如果奇函数 在区间
在区间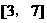 上是增函数且有最小值为5,那么
上是增函数且有最小值为5,那么 在区间
在区间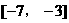 上是
上是
A. 增函数且最小值为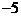 B.
增函数且最大值为
B.
增函数且最大值为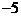
C. 减函数且最小值为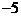 D.
减函数且最大值为
D.
减函数且最大值为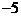
分析:画出满足题意的示意图1,易知选B。

图1
例6. 已知偶函数 在
在 上是减函数,问
上是减函数,问 在
在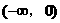 上是增函数还是减函数,并证明你的结论。
上是增函数还是减函数,并证明你的结论。
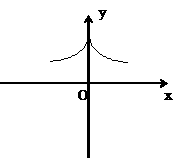
分析:如图2所示,易知 在
在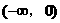 上是增函数,证明如下:
上是增函数,证明如下:
任取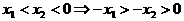
因为 在
在 上是减函数,所以
上是减函数,所以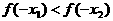 。
。
 又
又 是偶函数,所以
是偶函数,所以
 ,
,
从而 ,故
,故 在
在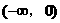 上是增函数。
上是增函数。
图2
2. 判断奇偶性
根据已知条件,通过恰当的赋值代换,寻求 与
与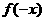 的关系。
的关系。
例3. 已知 的定义域为R,且对任意实数x,y满足
的定义域为R,且对任意实数x,y满足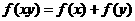 ,求证:
,求证: 是偶函数。
是偶函数。
分析:在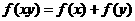 中,令
中,令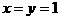 ,
,
得
令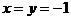 ,得
,得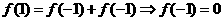
于是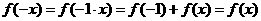
故 是偶函数。
是偶函数。
例4. 若函数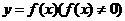 与
与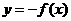 的图象关于原点对称,求证:函数
的图象关于原点对称,求证:函数
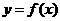 是偶函数。
是偶函数。
证明:设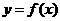 图象上任意一点为P(
图象上任意一点为P(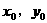 )
)
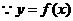 与
与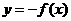 的图象关于原点对称,
的图象关于原点对称,
 关于原点的对称点
关于原点的对称点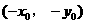 在
在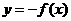 的图象上,
的图象上,
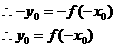
又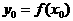
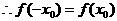
即对于函数定义域上的任意x都有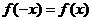 ,所以
,所以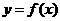 是偶函数。
是偶函数。
抽象函数的综合问题一般难度较大,常涉及到多个知识点,抽象思维程度要求较高,解题时需把握好如下三点:一是注意函数定义域的应用,二是利用函数的奇偶性去掉函数符号“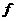 ”前的“负号”,三是利用函数单调性去掉函数符号“
”前的“负号”,三是利用函数单调性去掉函数符号“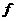 ”。
”。
例8 设函数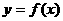 定义在R上,当
定义在R上,当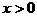 时,
时, ,且对任意
,且对任意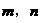 ,有
,有 ,当
,当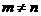 时
时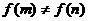 。
。
(1)证明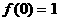 ;
;
(2)证明: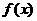 在R上是增函数;
在R上是增函数;
(3)设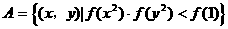 ,
,
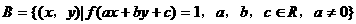 ,若
,若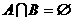 ,求
,求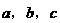 满足的条件。
满足的条件。
解:(1)令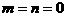 得
得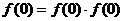 ,
,
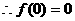 或
或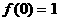 。
。
若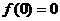 ,当
,当 时,有
时,有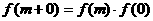 ,这与当
,这与当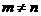 时,
时,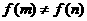 矛盾,
矛盾,
 。
。
(2)设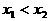 ,则
,则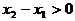 ,由已知得
,由已知得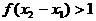 ,因为
,因为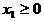 ,
,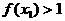 ,若
,若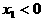 时,
时,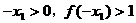 ,由
,由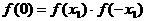
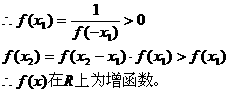
(3)由 得
得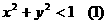
由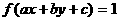 得
得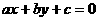 (2)
(2)
从(1)、(2)中消去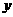 得
得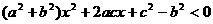 ,因为
,因为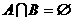
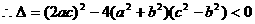 ,
,
即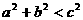
例9 定义在(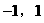 )上的函数
)上的函数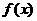 满足(1),对任意
满足(1),对任意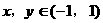 都有
都有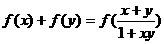 ,
,
(2)当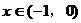 时,有
时,有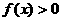 ,
,
(1)试判断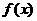 的奇偶性;(2)判断
的奇偶性;(2)判断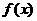 的单调性;
的单调性;
(3)求证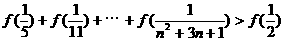 。
。
分析:这是一道以抽象函数为载体,研究函数的单调性与奇偶性,再以这些性质为基础去研究数列求和的综合题。
解:(1)对条件中的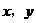 ,令
,令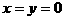 ,再令
,再令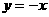 可得
可得
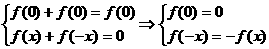 ,所以
,所以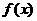 是奇函数。
是奇函数。
(2)设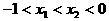 ,则
,则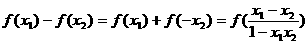
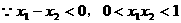 ,
,
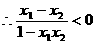 ,由条件(2)知
,由条件(2)知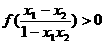 ,从而有
,从而有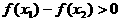 ,即
,即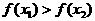 ,故
,故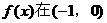 上单调递减,由奇函数性质可知,
上单调递减,由奇函数性质可知,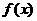 在(0,1)上仍是单调减函数。
在(0,1)上仍是单调减函数。
(3)
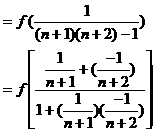
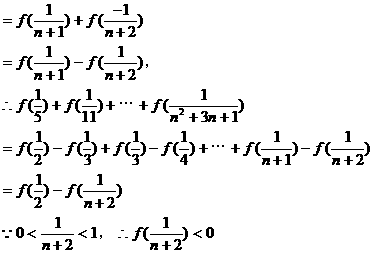
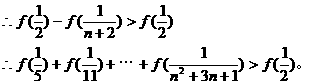
抽象函数问题分类解析
我们将没有明确给出解析式的函数称为抽象函数。近年来抽象函数问题频频出现于各类考试题中,由于这类问题抽象性强,灵活性大,多数同学感到困惑,求解无从下手。本文试图通过实例作分类解析,供学习参考。
1. 求定义域
这类问题只要紧紧抓住:将函数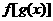 中的
中的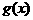 看作一个整体,相当于
看作一个整体,相当于 中的x这一特性,问题就会迎刃而解。
中的x这一特性,问题就会迎刃而解。
例1. 函数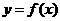 的定义域为
的定义域为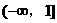 ,则函数
,则函数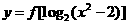 的定义域是___。
的定义域是___。
分析:因为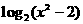 相当于
相当于 中的x,所以
中的x,所以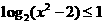 ,解得
,解得
 或
或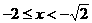 。
。
例2. 已知 的定义域为
的定义域为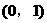 ,则
,则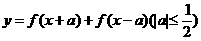 的定义域是______。
的定义域是______。
分析:因为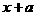 及
及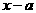 均相当于
均相当于 中的x,所以
中的x,所以
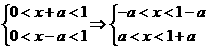
(1)当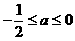 时,则
时,则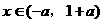
(2)当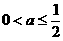 时,则
时,则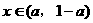
例6 设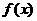 定义在R上且对任意的
定义在R上且对任意的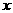 有
有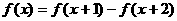 ,求证:
,求证: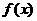 是周期函数,并找出它的一个周期。
是周期函数,并找出它的一个周期。
分析:这同样是没有给出函数表达式的抽象函数,其一般解法是根据所给关系式进行递推,若能得出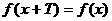 (T为非零常数)则
(T为非零常数)则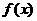 为周期函数,且周期为T。
为周期函数,且周期为T。
证明: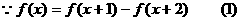
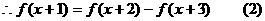
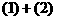 得
得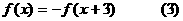
由(3)得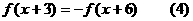
由(3)和(4)得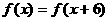 。
。
上式对任意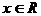 都成立,因此
都成立,因此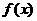 是周期函数,且周期为6。
是周期函数,且周期为6。
例7 已知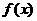 对一切
对一切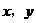 ,满足
,满足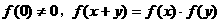 ,且当
,且当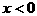 时,
时, ,求证:(1)
,求证:(1)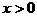 时,
时,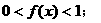 (2)
(2)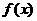 在R上为减函数。
在R上为减函数。
证明: 对一切
对一切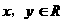 有
有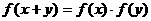 。
。
且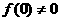 ,令
,令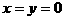 ,得
,得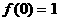 ,
,
现设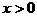 ,则
,则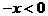 ,
,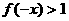 ,
,
而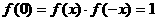
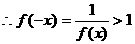
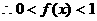 ,
,
设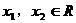 且
且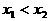 ,
,
则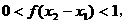
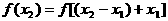

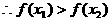 ,
,
即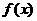 为减函数。
为减函数。
这类不等式一般需要将常数表示为函数在某点处的函数值,再通过函数的单调性去掉函数符号“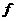 ”,转化为代数不等式求解。
”,转化为代数不等式求解。
例5 已知函数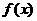 对任意
对任意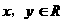 有
有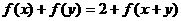 ,当
,当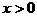 时,
时,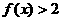 ,
,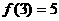 ,求不等式
,求不等式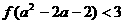 的解集。
的解集。
解:设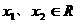 且
且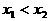
则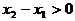
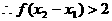 ,
,
即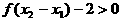 ,
,
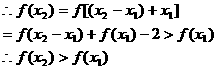
故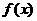 为增函数,
为增函数,
又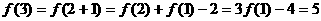
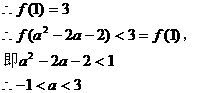
因此不等式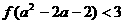 的解集为
的解集为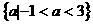 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com