
题目列表(包括答案和解析)
9.(全国I)(1)设函数 ,求
,求 的最小值;
的最小值;
(2)设正数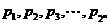 满足
满足 ,
,
求证:
(Ⅰ)解:对函数 求导数:
求导数: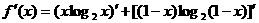

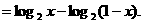
于是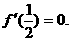
当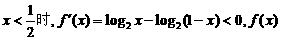 在区间
在区间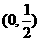 是减函数,
是减函数,
当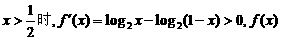 在区间
在区间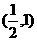 是增函数.
是增函数.
所以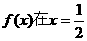 时取得最小值,
时取得最小值,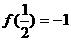 ,
,
(Ⅱ)证法一:用数学归纳法证明.
(i)当n=1时,由(Ⅰ)知命题成立.
(ii)假定当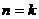 时命题成立,即若正数
时命题成立,即若正数 ,
,
则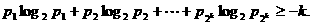
当 时,若正数
时,若正数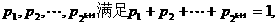
令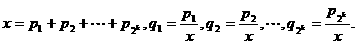
则 为正数,且
为正数,且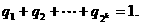
由归纳假定知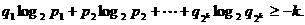

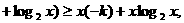 ①
①
同理,由 可得
可得
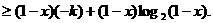 ②
②
综合①、②两式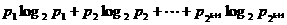
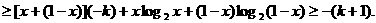
即当 时命题也成立.
时命题也成立.
根据(i)、(ii)可知对一切正整数n命题成立.
证法二:
令函数

利用(Ⅰ)知,当
对任意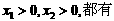

 . ①
. ①
下面用数学归纳法证明结论.
(i)当n=1时,由(I)知命题成立.
(ii)设当n=k时命题成立,即若正数

由①得到
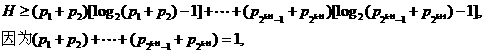
由归纳法假设
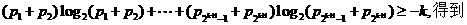
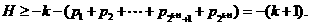
即当 时命题也成立.
时命题也成立.
所以对一切正整数n命题成立.
8.(江西卷)已知函数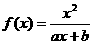 (a,b为常数)且方程f(x)-x+12=0有两个实根为x1=3,
x2=4.(1)求函数f(x)的解析式;
(a,b为常数)且方程f(x)-x+12=0有两个实根为x1=3,
x2=4.(1)求函数f(x)的解析式;
(2)设k>1,解关于x的不等式; .
.
解:(1)将 得
得

(2)不等式即为
即
①当
②当
③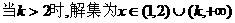 .
.
7.(浙江)已知函数f(x)和g(x)的图象关于原点对称,且f(x)=x2+2x.
(Ⅰ)求函数g(x)的解析式;
(Ⅱ)解不等式g(x)≥f(x)-|x-1|;
(Ⅲ)若h(x)=g(x)- f(x)+1在[-1,1]上是增函数,求实数
f(x)+1在[-1,1]上是增函数,求实数 的取值范围.
的取值范围.
解:(I)设函数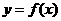 的图象上任一点
的图象上任一点 关于原点的对称点为
关于原点的对称点为 ,
,
则  即
即  .
.
∵点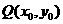 在函数
在函数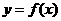 的图象上.
的图象上.

 即
即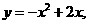 故g(x)=
故g(x)= .
.
(II)由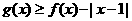 可得:
可得:
当
 1时,
1时,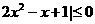
此时不等式无解。
当 时,
时,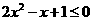

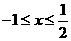
因此,原不等式的解集为[-1, 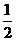 ].
].
(III) 
①
当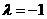 时,
时,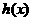 =
= 在[-1,1]上是增函数,
在[-1,1]上是增函数,

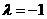
②当 时,对称轴的方程为
时,对称轴的方程为
(i) 当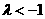 时,
时,
 ,解得
,解得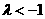 。
。
(ii) 当 时,
时,
 1时,解得
1时,解得
综上,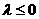
6.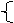 .[解](1)h(x)= (-2x+3)(x-2) x∈[1,+∞)
.[解](1)h(x)= (-2x+3)(x-2) x∈[1,+∞)
x-2 x∈(-∞,1)
(2) 当x≥1时, h(x)= (-2x+3)(x-2)=-2x2+7x-6=-2(x- )2+
)2+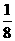
∴h(x)≤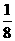 ;
;
当x<1时, h(x)<-1,
∴当x= 时, h(x)取得最大值是
时, h(x)取得最大值是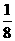
(3)令 f(x)=sinx+cosx,α=
则g(x)=f(x+α)= sin(x+ )+cos(x+
)+cos(x+ )=cosx-sinx,
)=cosx-sinx,
于是h(x)= f(x)·f(x+α)= (sinx+cosx)( cosx-sinx)=cos2x.
另解令f(x)=1+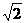 sinx, α=π,
sinx, α=π,
g(x)=f(x+α)=
1+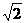 sin(x+π)=1-
sin(x+π)=1-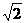 sinx,
sinx,
于是h(x)= f(x)·f(x+α)= (1+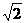 sinx)( 1-
sinx)( 1-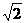 sinx)=cos2x.
sinx)=cos2x.
3. (北京卷)设f(x)是定义在[0, 1]上的函数,若存在x*∈(0,1),使得f(x)在[0, x*]上单调递增,在[x*,1]上单调递减,则称f(x)为[0, 1]上的单峰函数,x*为峰点,包含峰点的区间为含峰区间.对任意的[0,l]上的单峰函数f(x),下面研究缩短其含峰区间长度的方法.
(I)证明:对任意的x1,x2∈(0,1),x1<x2,若f(x1)≥f(x2),则(0,x2)为含峰区间;若f(x1)≤f(x2),则(x*,1)为含峰区间;
(II)对给定的r(0<r<0.5),证明:存在x1,x2∈(0,1),满足x2-x1≥2r,使得由(I)所确定的含峰区间的长度不大于 0.5+r;
(III)选取x1,x2∈(0, 1),x1<x2,由(I)可确定含峰区间为(0,x2)或(x1,1),在所得的含峰区间内选取x3,由x3与x1或x3与x2类似地可确定一个新的含峰区间.在第一次确定的含峰区间为(0,x2)的情况下,试确定x1,x2,x3的值,满足两两之差的绝对值不小于0.02,且使得新的含峰区间的长度缩短到0.34.(区间长度等于区间的右端点与左端点之差)
解:(I)证明:设x*为f(x) 的峰点,则由单峰函数定义可知,f(x)在[0, x*]上单调递增,在[x*, 1]上单调递减.
当f(x1)≥f(x2)时,假设x* (0, x2),则x1<x2<x*,从而f(x*)≥f(x2)>f(x1),
(0, x2),则x1<x2<x*,从而f(x*)≥f(x2)>f(x1),
这与f(x1)≥f(x2)矛盾,所以x*∈(0, x2),即(0, x2)是含峰区间.
当f(x1)≤f(x2)时,假设x* ( x2, 1),则x*<≤x1<x2,从而f(x*)≥f(x1)>f(x2),
( x2, 1),则x*<≤x1<x2,从而f(x*)≥f(x1)>f(x2),
这与f(x1)≤f(x2)矛盾,所以x*∈(x1, 1),即(x1, 1)是含峰区间.
(II)证明:由(I)的结论可知:
当f(x1)≥f(x2)时,含峰区间的长度为l1=x2;
当f(x1)≤f(x2)时,含峰区间的长度为l2=1-x1;
对于上述两种情况,由题意得
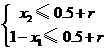 ①
①
由①得 1+x2-x1≤1+2r,即x1-x1≤2r.
又因为x2-x1≥2r,所以x2-x1=2r, ②
将②代入①得
x1≤0.5-r, x2≥0.5-r, ③
由①和③解得 x1=0.5-r, x2=0.5+r.
所以这时含峰区间的长度l1=l1=0.5+r,即存在x1,x2使得所确定的含峰区间的长度不大于0.5+r.
(III)解:对先选择的x1;x2,x1<x2,由(II)可知
x1+x2=l, ④
在第一次确定的含峰区间为(0, x2)的情况下,x3的取值应满足
x3+x1=x2, ⑤
由④与⑤可得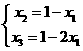 ,
,
当x1>x3时,含峰区间的长度为x1.
由条件x1-x3≥0.02,得x1-(1-2x1)≥0.02,从而x1≥0.34.
因此,为了将含峰区间的长度缩短到0.34,只要取
x1=0.34,x2=0.66,x3=0.32.
4(上海)已知函数f(x)=kx+b的图象与x、y轴分别相交于点A、B,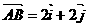 (
( 、
、 分别是与x、y轴正半轴同方向的单位向量), 函数g(x)=x2-x-6.
分别是与x、y轴正半轴同方向的单位向量), 函数g(x)=x2-x-6.
(1)求k、b的值;
(2)当x满足f(x)>
g(x)时,求函数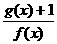 的最小值.
的最小值.
[解](1)由已知得A(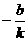 ,0),B(0,b),则
,0),B(0,b),则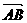 ={
={ ,b},于是
,b},于是 =2,b=2. ∴k=1,b=2.
=2,b=2. ∴k=1,b=2.
(2)由f(x)> g(x),得x+2>x2-x-6,即(x+2)(x-4)<0, 得-2<x<4,
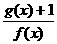 =
= =x+2+
=x+2+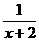 -5
-5
由于x+2>0,则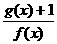 ≥-3,其中等号当且仅当x+2=1,即x=-1时成立
≥-3,其中等号当且仅当x+2=1,即x=-1时成立
∴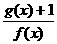 的最小值是-3.
的最小值是-3.
5,(上海)(本题满分18分)本题共有3个小题,第1小题满分4分, 第2小题满分8分, 第3小题满分6分.
对定义域分别是Df、Dg的函数y=f(x) 、y=g(x),
 f(x)·g(x) 当x∈Df且x∈Dg
f(x)·g(x) 当x∈Df且x∈Dg
规定: 函数h(x)= f(x)
当x∈Df且x Dg
Dg
g(x) 当x Df且x∈Dg
Df且x∈Dg
(1) 若函数f(x)=-2x+3,x≥1; g(x)=x-2,x∈R,写出函数h(x)的解析式;
(2) 求问题(1)中函数h(x)的最大值;
(3) 若g(x)=f(x+α), 其中α是常数,且α∈[0,π],请设计一个定义域为R的函数y=f(x),及一个α的值,使得h(x)=cos2x,并予以证明.
2. (全国卷Ⅰ)已知二次函数 的二次项系数为
的二次项系数为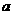 ,且不等式
,且不等式 的解集为
的解集为 。(Ⅰ)若方程
。(Ⅰ)若方程 有两个相等的根,求
有两个相等的根,求 的解析式;
的解析式;
(Ⅱ)若 的最大值为正数,求
的最大值为正数,求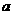 的取值范围。
的取值范围。
解:(Ⅰ)
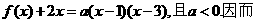
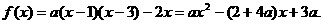 ①
①
由方程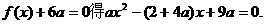 ②
②
因为方程②有两个相等的根,所以 ,
,
即 
由于 代入①得
代入①得 的解析式
的解析式

(Ⅱ)由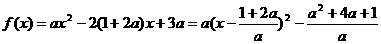
及
由 解得
解得 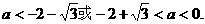
故当 的最大值为正数时,实数a的取值范围是
的最大值为正数时,实数a的取值范围是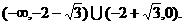
1、(广东卷)设函数 在
在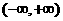 上满足
上满足 ,
, ,且在闭区间[0,7]上,只有
,且在闭区间[0,7]上,只有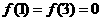 .
.
(Ⅰ)试判断函数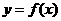 的奇偶性;
的奇偶性;
(Ⅱ)试求方程 =0在闭区间[-2005,2005]上的根的个数,并证明你的结论.
=0在闭区间[-2005,2005]上的根的个数,并证明你的结论.
.解:由f(2-x)=f(2+x),f(7-x)=f(7+x)得函数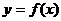 的对称轴为
的对称轴为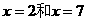 ,
,
从而知函数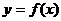 不是奇函数,
不是奇函数,
由
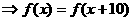 ,从而知函数
,从而知函数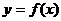 的周期为
的周期为
又 ,故函数
,故函数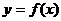 是非奇非偶函数;
是非奇非偶函数;
(II)由
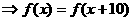
(II) 又
故f(x)在[0,10]和[-10,0]上均有有两个解,从而可知函数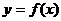 在[0,2005]上有402个解,在[-2005.0]上有400个解,所以函数
在[0,2005]上有402个解,在[-2005.0]上有400个解,所以函数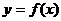 在[-2005,2005]上有802个解.
在[-2005,2005]上有802个解.
13.(浙江)函数y= (x∈R,且x≠-2)的反函数是
(x∈R,且x≠-2)的反函数是 .
.
解答题:
12. (江西卷)若函数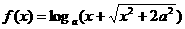 是奇函数,则a=
.
是奇函数,则a=
.
11. (天津卷)设f(x)是定义在R上的奇函数,且y=f (x)的图象关于直线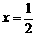 对称,则f (1)+ f (2)+ f (3)+ f
(4)+ f (5)=_0_______________.
对称,则f (1)+ f (2)+ f (3)+ f
(4)+ f (5)=_0_______________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com