
题目列表(包括答案和解析)
5.(天津卷)设集合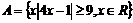 ,
,  , 则A∩B= (D)
, 则A∩B= (D)
A.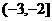 B.
B. C.
C. D.
D.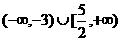
4、(上海卷)已知集合 ,
,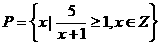 ,则
,则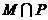 等于
(B)
等于
(B)
A. B.
B.
C. D.
D.
3.(北京卷)“m= ”是“直线(m+2)x+3my+1=0与直线(m-2)x+(m+2)y-3=0相互垂直”的
(B)
”是“直线(m+2)x+3my+1=0与直线(m-2)x+(m+2)y-3=0相互垂直”的
(B)
(A)充分必要条件 (B)充分而不必要条件
(C)必要而不充分条件 (D)既不充分也不必要条件
2.(北京卷)设全集U=R,集合M={x| x>1,P={x| x2>1},则下列关系中正确的是(C)
(A)M=P (B)P M
(C)M
M
(C)M P
( D)
P
( D)
1.(全国卷Ⅰ)设 为全集,
为全集,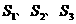 是
是 的三个非空子集,且
的三个非空子集,且 ,则下面论断正确的是(C)
,则下面论断正确的是(C)
(A)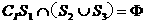 (B)
(B)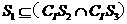
(C) (D)
(D)
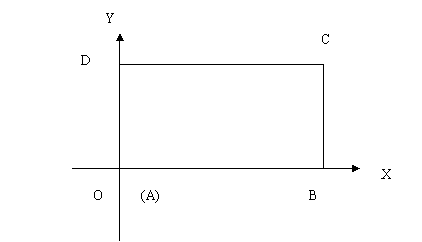
2.(广东卷)在平面直角坐标系中,已知矩形ABCD的长为2,宽为1,AB、AD边分别在x轴、y轴的正半轴上,A点与坐标原点重合(如图5所示).将矩形折叠,使A点落在线段DC上.
(Ⅰ)若折痕所在直线的斜率为k,试写出折痕所在直线的方程;
(Ⅱ)求折痕的长的最大值.

.解(I) (1)当 时,此时A点与D点重合, 折痕所在的直线方程
时,此时A点与D点重合, 折痕所在的直线方程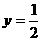
(2)当 时,将矩形折叠后A点落在线段CD上的点为G(a,1)
时,将矩形折叠后A点落在线段CD上的点为G(a,1)
所以A与G关于折痕所在的直线对称,有
故G点坐标为 ,从而折痕所在的直线与OG的交点坐标(线段OG的中点)为
,从而折痕所在的直线与OG的交点坐标(线段OG的中点)为
折痕所在的直线方程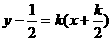 ,即
,即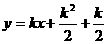
由(1)(2)得折痕所在的直线方程为:
k=0时,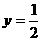 ;
; 时
时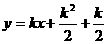
(II)(1)当 时,折痕的长为2;
时,折痕的长为2;
(1)
当 时, 折痕所在的直线与坐标轴的交点坐标为
时, 折痕所在的直线与坐标轴的交点坐标为


令 解得
解得 ∴
∴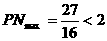
所以折痕的长度的最大值2
1. (江苏卷) 如图,圆O1与圆O2的半径都是1,O1O2=4,过动点P分别作圆O1、圆O2的切线PM、PN(M、N分别为切点),使得
(江苏卷) 如图,圆O1与圆O2的半径都是1,O1O2=4,过动点P分别作圆O1、圆O2的切线PM、PN(M、N分别为切点),使得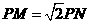 试建立适当的坐标系,并求动点 P的轨迹方程.
试建立适当的坐标系,并求动点 P的轨迹方程.
解:如图,以直线 为
为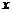 轴,线段
轴,线段 的垂直平分线为
的垂直平分线为 轴,建立平面直角坐标系,则两圆心分别为
轴,建立平面直角坐标系,则两圆心分别为 .设
.设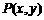 ,则
,则 ,同理
,同理 .
.
∵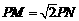 ,
,
∴ ,
,
即 ,即
,即 .这就是动点
.这就是动点 的轨迹方程.
的轨迹方程.
10.(山东卷)设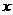 、
、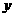 满足约束条件
满足约束条件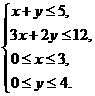 则使得目标函数
则使得目标函数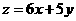 的最大的点
的最大的点 是(2,3).
是(2,3).
解答题
9.(上海)将参数方程 (
(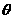 为参数)化为普通方程,所得方程是_ (x-1)2+y2=4 _________。
为参数)化为普通方程,所得方程是_ (x-1)2+y2=4 _________。
4.(湖北卷)某实验室需购某种化工原料106千克,现在市场上该原料有两种包装,一种是每袋35千克,价格为140元;另一种是每袋24千克,价格为120元. 在满足需要的条件下,最少要花费 500 元.
5 (福建卷)15.非负实数x、y满足 的最大值为 9 .
的最大值为 9 .
6(江西卷)设实数x, y满足
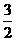 .
.
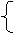 7(上海)3.若x,y满足条件 x+y≤3
7(上海)3.若x,y满足条件 x+y≤3
y≤2x ,则z=3x+4y的最大值是 11 .
8(上海)直线y=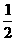 x关于直线x=1对称的直线方程是 x+2y-2=0
.
x关于直线x=1对称的直线方程是 x+2y-2=0
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com