21．(本小题满分12分)

　 　设动点P到点A(－l，0)和B(1，0)的距离分别为d₁和d₂，

　 　∠APB＝2θ，且存在常数λ(0＜λ＜1)，使得d₁d₂ sin²θ＝λ．

　 　(1)证明：动点P的轨迹C为双曲线，并求出C的方程；

　 (2)过点B作直线交双曲线C的右支于M、N两

　 　　　点，试确定λ的范围，使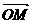·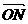＝0，其中点

　　 　　O为坐标原点．

20．(本小题满分12分)

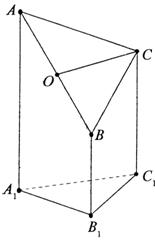
　 　右图是一个直三棱柱(以A₁B₁C₁为底面)被一平面所截得到

　 　的几何体，截面为ABC．已知A₁B₁＝B₁C₁＝l，∠A_lB_lC₁＝90°，

　 　AA_l＝4，BB_l＝2，CC_l＝3．

　 　(1)设点O是AB的中点，证明：OC∥平面A₁B₁C₁；

　 　(2)求二面角B-AC-A₁的大小；

　 　(3)求此几何体的体积．

19．(本小题满分12分)

　 　某陶瓷厂准备烧制甲、乙、丙三件不同的工艺品，制作过程必须先后经过两次烧制，当第一次烧制合格后方可进入第二次烧制，两次烧制过程相互独立．根据该厂现有的技术水平，经过第一次烧制后，甲、乙、丙三件产品合格的概率依次为0.5，　 0.6，　 0.4．经过第二次烧制后，甲、乙、丙三件产品合格的概率依次为0.6，0.5，0.75．

　 　(1)求第一次烧制后恰有一件产品合格的概率；

　 　(2)经过前后两次烧制后，合格工艺品的个数为ξ，求随机变量ξ的期望．

18．(本小题满分12分)

如图，函数y＝2cos(ωx+θ) (x∈R，0≤θ≤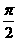)的

图象与y轴交于点(0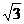，)，且在该点处切线的斜

率为一2．

　 　(1)求θ和ω的值；

　 　(2)已知点A(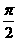，0)，点P是该函数图象上一点，点Q(x₀，y₀)是PA的中点，当y₀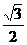＝，x∈[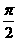，π]时，求x₀的值．

17．(本小题满分12分)

　 　已知函数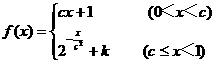在区间(0，1)内连续，且．

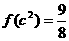　 　(1)求实数k和c的值；

　 　(2)解不等式

16．设有一组圆C_k：(x－k+1)²+(y－3k)²＝2k⁴ (k∈N^*)．下　

列四个命题：　

A．存在一条定直线与所有的圆均相切

B．存在一条定直线与所有的圆均相交

C．存在一条定直线与所有的圆均不相交

D．所有的圆均不经过原点

其中真命题的代号是　　 ．(写出所有真命题的代号)

15．如图，在△ABC中，点O是BC的中点，过点O的直

线分别交直线AB、AC于不同的两点M、N，若＝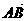

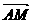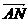m，＝n，则m+n的值为　　　　　 ．

14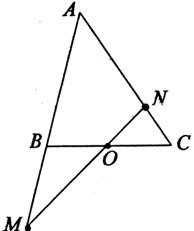．已知数列{a_n}对于任意p，q ∈N^*，有a_p+a_q=a_p+q，若a₁=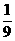，则a₃₆＝　　　　 ．

13．设函数y＝4+log₂(x－1)(x≥3)，则其反函数的定义域为　　　　　 ．

12．设p：f(x)＝e^x+In x+2x²+mx+l在(0，+∞)内单调递增，q：m≥－5，则p是q的

　 　A．充分不必要条件　 　　　　　　B．必要不充分条件

　 　C．充分必要条件　　 　　　　　　D．既不充分也不必要条件

绝密★启用前

2007年普通高等学校招生全国统一考试(江西卷)

理科数学

第Ⅱ卷

　 　第Ⅱ卷2页，须用黑色墨水签字笔在答题卡上书写作答．若在试题卷上作答，答案无效．