
题目列表(包括答案和解析)
20. 已知函数 在
在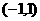 上有意义,
上有意义, ,且满足
,且满足 、
、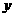
 时,有
时,有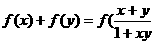 )
)
(1)证明 在
在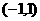 上是奇函数;
上是奇函数;
(2)对数列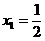 ,
, ,求
,求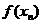 ;
;
(3)对于(2)中的数列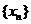 ,求证:
,求证:
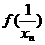
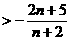 .
.
19. 已知函数
(1)若函数 在[1,2]上是减函数,在[3,4]上是增函数,求实数
在[1,2]上是减函数,在[3,4]上是增函数,求实数 的取值范围.
的取值范围.
(2)若直线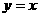 是函数
是函数 图象的切线,求
图象的切线,求 的值.
的值.
18. 已知正三棱柱A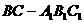 的每条棱长都为
的每条棱长都为 ,
,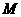 为棱
为棱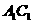 上的动点.
上的动点.
(1)求三棱锥 体积的最大值.
体积的最大值.
(2)当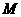 在何处时,
在何处时,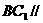 平面
平面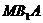 ,并证明;
,并证明;
(3)在(2)的条件下,求平面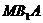 与侧面
与侧面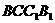 所成锐二面角的大小.
所成锐二面角的大小.
17. 已知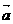
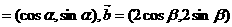 ,且
,且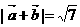
(1)求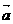 与
与 的夹角;
的夹角;
(2)若 ,且
,且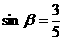 ,求
,求 .
.
16. 已知 ,则
,则 的最小值为_______.
的最小值为_______.
15.实数 、
、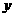 满足不等式组
满足不等式组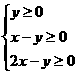 ,则
,则 的取值范围是_____.
的取值范围是_____.
14. 给出下列四个命题
①过平面外一点作与该平面成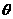 角的直线一定有无穷多条;
角的直线一定有无穷多条;
②一条直线与两个相交平面都平行,则它与这两个平面的交线平行;
③对确定的两条异面直线,过空间任意一点有且只有一个平面与这两条异面直线都平行;
④对确定的两条异面直线都存在无穷多个平面与这两条异面直线所成的角相等。
其中正确命题的序号是__________.
13.坐标平面内,点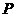 与两个定点
与两个定点 连线的斜率之积为常数
连线的斜率之积为常数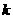 ,当
,当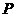 点轨迹是一条准线方程为
点轨迹是一条准线方程为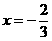 的双曲线时,
的双曲线时,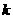 的值为______.
的值为______.
12. 甲、乙两人进行五盘三胜制的象棋赛,若甲每盘的获胜概率为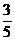 ,乙每盘获胜的概率为
,乙每盘获胜的概率为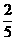 (和棋不算),则比赛以甲比乙为3比1胜出的概率为______.
(和棋不算),则比赛以甲比乙为3比1胜出的概率为______.
11.已知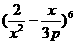 展开式中
展开式中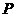 的常数项为
的常数项为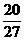 ,则
,则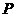 的值为_______.
的值为_______.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com