1．不等式1≤|2x－1|<2的解集为　　　　　　　　　　　　　　　　　 。

4．应用绝对值不等式的性质对不等式进行放和缩，并能对不等式进行证明。

基本方法：分类讨论、数形结合、平方法

重点难点

重点：含绝对值不等式的解法

难点：绝对值不等式的性质的运用以及含参数的一些绝对值不等式的讨论。

基础练习

3．能利用讨论的方法解含有多个绝对值的不等式

2．能够利用绝对值的几何意义和平方法解含有绝对值的不等式

3．　 掌握简单的含绝对值不等式的解法。

知识概要

知识点：1．掌握两类最简的绝对值不等式：1⁰|f(x)| ≥a (a>0)f(x)≤－a或f(x)≥a；

2⁰ |f(x)| ≤a (a>0) －a≤f(x)≤a

2．　 理解绝对值不等式的性质：|a|－|b|≤|a±b|≤|a|+|b|，弄清其中等号成立的条件。

1．　 理解绝对值的含义

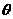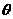10．已知cos²+msin－2>0在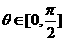上恒成立，求m的取值范围。

　　　　　　 　第六章　 不等式

　　　　　　　　　　　　　　　　　　 班级　　　　 学号　　　 姓名　　　　　

第八课时　　　 含有绝对值的不等式

考纲摘录

9．关于x的不等式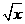>ax+的解集为(4，b)，求a,b的值。

8．已知不等式组 的解集是不等式2x²－9x+a<0的解集的子集，求实数a的取值范围。