1、两个概念、排列的定义、组合的定义；

8、设集合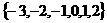，P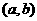是坐标平面上的点，、．

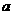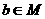(1)P可以表示多少个平面上的不同的点？

(2)P可以表示多少个第二象限内的点？

　(3)P可以表示多少个不在直线y=x上的点？

高三数学教学案　　　　　 　　 第十章　 排列、组合、二项式定理

第二课时　 排列与组合(一)

考纲摘录

理解排列与组合的意义，掌握排列数与组合数的计算公式，掌握组合数的两个性质，

并能运用它们解决一些简单的应用问题．

知识概要

7、三边长均为整数，且最大边长为11的三角形有多少个．

6、从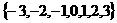中任取3个不同的数作为抛物线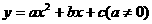的系数，如果抛物线过原点且顶点在第一象限，则这样的抛物线有多少条？

5、在所有的两位数中：个位数字小于十位数字的两位数共有_______个．

4、将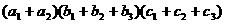展开后的项数是______________．

3、从集合P={0，1，2，3，4}，从中任取两个不同的数作为A、B的值，得到直线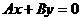一共可得多少条不同的直线．

2、648的正约数有______________个．

1、4封不同的信投入4个不同的信箱，有________种不同的投法，若要求每个信箱投入一封信，则有________种不同的投法．

5、从5门不同的文科学科，与4门不同的理科学科中任选4门，组成一组综合文科目组，若要求这组科目中，文、理科都有，则不同的选法种数是　　　　　　　　　　　　　　　　　　　 (　 )

A．60种　　　  B．80种  C．120种　　　  D．140种

例题讲解

例1、4位同学报名参加数理化竞赛，每人规定报一科，有________种报名方法．

例2、已知集合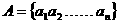 ，求

(1)集合A的子集的个数；

(2)集合B到集合A的不同映射的个数．

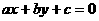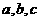例3、已知直线中的是取自集合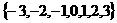中的3个不同的元素，并且该直线的倾斜角为锐角，那么这样直线的条数是__________．

例4、在如图的1×6的矩形长条中，涂上红、黄、蓝3种颜色，每种颜色限涂2格，并且相邻两格不同色，则不同的涂色方法共有多少种？

课后作业

　　　　　　　　　　　　　　　　　　　　　　　 班级_______学号__________姓名_________