4、的图象与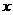轴围成的图形的面积是_________．

例题讲解

例1、已知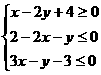，试求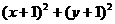的最大、最小值．

例2、设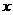、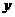满足和．

(1)求点(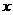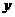，)所表示的平面区域；

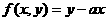(2)设，在(1)所确定的区域里，求函数的最大值和最小值．

例3、长江三峡电厂4台机组发电，每台机组日最大发电量为0.168亿度，每度电输送成本为0.32元，与此同时长江葛州坝电厂有8台机组发电，每台机组日最大发电量为0.12亿度，每度电输送成本为0.35元，由于高温和工业生产，江浙地区用电量增大，日增需求量至少为1.35亿度．

(1)设电力调度总指挥安排三峡电厂有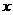台机组发电，葛州坝电厂有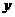台机组发电，输送江浙地区以填补电力缺口，长江电力公司输送成本为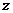亿元，写出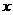、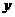应满足的条件及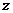与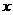、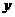间的函数关系式；

(2)假设你是长江电力公司总经理，为使公司电力输送成本最小，每天如何安排两大电厂的机组数，才可以满足江浙地区用电日增需求量．

课后作业

　　　　　　　　　　　　　　　　　　　　　　　 班级_______学号__________姓名_________

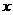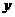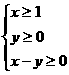3、、满足，则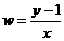的取值范围是____________．

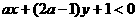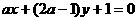2、表直线的下方，则___________．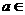

1、给出平面区域如图，如果目标函数取得最大值的最优解有无穷多个，那么实数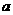的值是________．

8、某工厂的一个车间生产某种产品，其成本为每千克27元，售价为每千克50元．在生产产品的同时，每千克新产品产生出0.3m³的污水，污水有两种排放方式：其一是输送到污水处理厂；其二是直接排入河流．若污水处理厂每小时最大处理能力是0.9m³，处理成本为5元/m³,而且只能净化污水的85%，未净化的污水仍排入河流，环保部门对排入河流的污水收费标准是17.6元/m³，根据环保要求该车间每小时最多允许排入河流中的污水是0.225m³．试问：该车间应选择怎样的生产与排污方案，使其净收益最大．

高三数学教学案　　　　　 　　 第七章　 直线和圆的方程

第五课时　 线性规划(二)

目标要求

　　　 线性规划的灵活运用．

基础练习

7、已知甲、乙两煤矿的日产量分别是200吨和100吨，两矿生产的煤需经、，车站运往外地，若、两车站分别最多只能接受160吨．已知甲、乙两矿运往、车站的运输价格如表所示，问如何安排运输方案，可使运输费用最低．

车　 站 价格(元/吨) 　 煤 矿
甲	20	18
乙	15	10

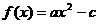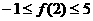6、已知函数满足，，求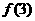的取值范围．

5、实系数方程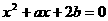的一个根大于0且小于1，另一个根大于1且小于2，则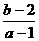的取值范围是___________．

4、画出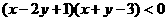表示的平面区域．

3、三个点、、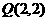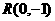中，落在由方程确定的曲线所围成区域中的个数有____________．