
题目列表(包括答案和解析)
1、已知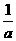 <
< <0,则下列不等式中:①a+b<ab ②| a |>| b | ③ a<b ④
<0,则下列不等式中:①a+b<ab ②| a |>| b | ③ a<b ④ >2,正确的不等式个数是________个.
>2,正确的不等式个数是________个.
4、若 ,
,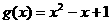 且
且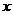 <1,则
<1,则 与
与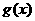 的大小关系是____________.
的大小关系是____________.
例题讲解
例1、已知三个不等式:ab>0,bc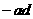 >0,
>0,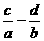 >0(其中a、b、c、d均为实数)用其中两个不等式作为条件,余下的一个不等式作为结论组成一个命题,确定可组成的正确命题.
>0(其中a、b、c、d均为实数)用其中两个不等式作为条件,余下的一个不等式作为结论组成一个命题,确定可组成的正确命题.
例2、(1)若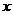 <
<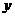 <0,试比较
<0,试比较 与
与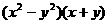 的大小
的大小
(2)设a>0,b>0且a≠b,试比较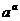 ·
·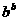 与
与 ·
·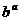 的大小。
的大小。
例3、在等比数列{an}和等差数列{bn}中,a1=b1>0,a3=b3>0,且a1≠a3,试比较a2与b2、、、、a5与b5的大小.
例4、设 ,且1≤
,且1≤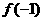 ≤2,2≤
≤2,2≤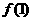 ≤4,求
≤4,求 的取值范围。
的取值范围。
课后作业
班级_______学号__________姓名_________
3、(1)若3≤m<6,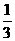 m<n<2m,则m+n取值范围是_____________.
m<n<2m,则m+n取值范围是_____________.
(2)若角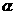 、
、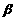 满足
满足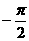 <
<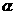 <
<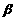 <
<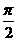 ,则2
,则2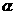
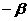 取值范围是_____________.
取值范围是_____________.
2、若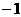 <a<b<0,则有 ( )
<a<b<0,则有 ( )
A. <
<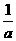 <b2<a2
B.
<b2<a2
B. <
<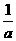 <a2<b2
<a2<b2
C.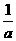 <
< <b2<a2 D.
<b2<a2 D.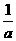 <
< <a2<b2
<a2<b2
1、设a、b、c∈R,判断下列各命题的真假
1)若a>b,则ac2>bc2 2)若ac2>bc2,则a>b
3)若a<b<0,则a2>ab>b2 4)若a<b<0,则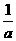 <
<
5)若a<b<0,则|a | >| b | 6)若c>a>b>0,则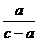 >
>
7)若a<b<0,则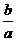 >
>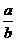 8)若a>b,
8)若a>b,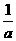 >
> 则a>0,b<0
则a>0,b<0
2、不等式的性质
基本方法:比较两个代数值(或式)的大小:作差比较法与作商比较法.
重点难点
重点:不等式的性质和比较法的应用.
难点:不等式性质及推论的证明.
基础练习
3、能正确使用不等式的性质,进行两个代数式大小的比较,以及判定某些不等式是否成立。
知识概要
知识点:1、实数的运算性质
2、理解不等式的性质定理及其推论的证明;
1、掌握实数的运算性质及大小顺序之间的关系;
7、已知动圆过定点P(1,0),且与定直线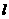 :
: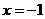 相切,点C在
相切,点C在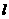 上,
上,
(1)求动圆圆心的轨迹M的方程;
(2)设过点P,且斜率为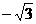 的直线与曲线M相交于A、B两点
的直线与曲线M相交于A、B两点
①问:△ABC能否为正三角形?若能,求出点C的坐标3,若不能,请说明理由.
②当△ABC为钝角三角形时,求这种点C的纵坐标的取值范围.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com