8、已知E、F分别是正方体ABCD－A₁B₁C₁D₁的棱AA₁、CC₁上的点，且AE=C₁F，求证：四边形EBFD₁是平行四边形．

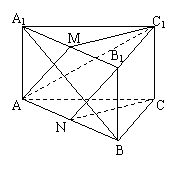
7、直三棱柱ABC－A₁B₁C₁中，B₁C₁= A₁C₁，AC₁⊥A₁B，M、N分别是A₁B₁，AB的中点，

(1)求证：C₁M⊥平面A₁ABB₁；

(2)求证：A₁B⊥AM；

(3)求证：平面AMC₁∥平面NB₁C．

6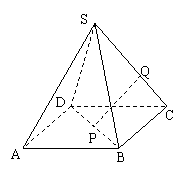．如图，正四棱锥S－ABCD的底面边长为a，侧棱长为2a，点P、Q分别在BD和SC上，并且BP:PD=1:2，PQ∥平面SAD，求线段PQ的长．

5．如图，正三棱柱ABC－A₁B₁C₁的底面边长为2，侧棱长为，D为B₁C₁的中点

(1)求异面直线AC₁与BD夹角；

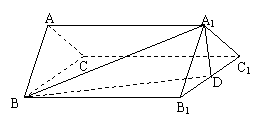(2)判定AC₁与平面A₁BD的位置关系并证明．

4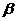．、是两个不重合的平面，在下列条件中，可判定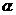∥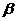的是(　 )

A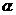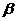．、都垂直于平面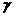　　　　　　　

B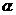．内不共线的三点到平面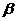的距离相等

C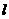．、m是平面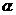内的直线，且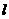∥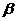，m∥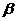

D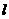．、m是两条异面直线，且均与平面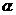、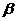平行

3．一条直线和一个平面平行，过此直线和这个平面平行的平面有_______个．

2．有下列四个命题：

①分别在两个平行平面内的两条直线都平行；

②若两个平面平行，则其中一个平面内的直线必平行于另一个平面；

③如果一个平面内的两条直线平行于另一个平面，则这两个平面平行；

④如果一个平面内的任何一条直线都平行于另一个平面，则这两个平面平行．

其中正确命题的序号为__________．

1．已知直线m、n及平面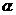，其中m∥n，那么在平面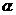内到两条直线m、n距离相等的点的集合是(　 )

　　　 A．一条直线 　　　 B．一个平面　　　　 C．空集 　　　　　　　 D．以上都有可能

4．在正四棱柱ABCD－A₁B₁C₁D₁中，E、F、G、H分别为棱CC₁，C₁D₁，D₁D，DC的中点，N是BC的中点，点M在四边形EFGH及其内部运动，则M满足条件________时，有MN∥平面B₁BDD₁．

例题讲解

例1．已知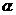平面∥平面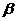，AB、CD是异面直线，A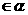、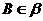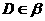，，，E、F分别为AB、CD的中点，

求证：EF∥∥．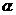

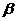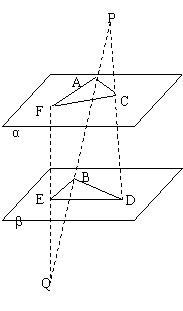
例2．直线PQ分别交两平行平面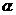、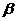于A、B两点，直线PD分别交平面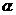、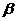于C、D两点，直线QF分别交平面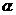、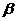于F、E两点，若PA=9，AB=12，QB=6，S_△ACF=72，求S_△BDE．

例4、三个平面两两相交有三条交线，这三条交线或交于一点或互相平行．

课后作业

　　　　　　　　　　　　 班级　　　　 学号　　　 姓名　　　　　

3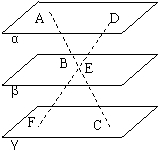．直线AC、DF被三个平行平面、、

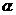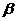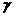
所截，若AC与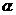成30°，AB=4，BC=12，

DF=10，则平面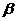、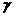间距离为________，

DE=________，EF=_______．