
题目列表(包括答案和解析)
1、在正四面体ABCD中,E为棱AD中点,则CE与平面BCD所成角的正弦值为__________.
4、有一个三角尺ABC,∠A=30°,∠C=90°,BC贴于桌面上,当三角尺与桌面成45°角时,AB边与桌面所成角的正弦值是__________.
例题讲解
 例1、如图,在正方体AC1中,(1)求BC1与平面ACC1A1所成的角; (2)求A1B1与平面A1C1B所成的角.
例1、如图,在正方体AC1中,(1)求BC1与平面ACC1A1所成的角; (2)求A1B1与平面A1C1B所成的角.
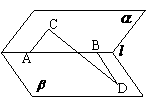
例2、已知二面角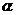 -
-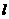 -
-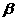 为60°,
为60°,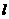 上有两点A、B,线段AC,BD分别在面
上有两点A、B,线段AC,BD分别在面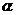 、
、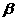 内,且AC⊥AB,BD⊥AB,AB=4,AC=6,BD=8,
内,且AC⊥AB,BD⊥AB,AB=4,AC=6,BD=8,
(1)求CD的长; (2)求异面直线CD与AB所成的角;
(3)求CD与平面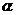 所成的角.
所成的角.
例3、在四面体S-ABC中,SA,SB,SC两两垂直,∠SBA=45°,∠SBC=60°,M为AB的中点,求:(1)BC与平面SAB所成角; (2)SM与平面ABC所成角的余弦值.

课后作业
班级_______学号__________姓名_________
3、∠AOB在平面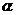 内,OC是
内,OC是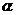 的斜线,OB为OC在平面
的斜线,OB为OC在平面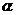 内的射影,若∠COA=
内的射影,若∠COA=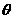 ,∠COB=
,∠COB=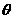 1,∠BOA=
1,∠BOA=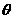 2,则
2,则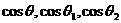 三者之间满足的关系式是___________.
三者之间满足的关系式是___________.
2、若线段AB夹在两个互相垂直的平面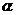 、
、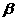 间,AB与
间,AB与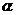 成
成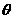 角,AB与
角,AB与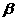 成
成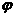 角,则
角,则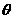 +
+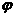 的值的范围
(
)
的值的范围
(
)
A.0°<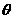 +
+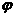 ≤90° B.0°<
≤90° B.0°<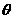 +
+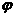 < 90°
< 90°
C.90°≤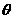 +
+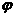 <180° D.以上都不对
<180° D.以上都不对
1、两条直线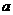 ,
,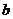 与平面
与平面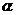 所成的角相等,则
所成的角相等,则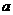 ,
,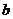 的位置关系是
( )
的位置关系是
( )
A.平行 B.相交 C.异面 D.以上均可能
2、求直线与平面所成角的关键是作垂直,找射影.
重点难点
如何作垂直定射影,从而构成直角三角形,并能够求出角.
基础练习
1、斜线与平面所成角的定义,空间直线与平面所成角的范围;
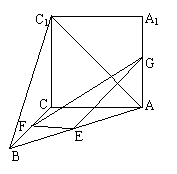
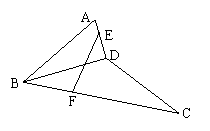
8、如图,正方形ACC1A1与等腰直角△ACB所在平面互相垂直,且AC=BC=2,E、F、G分别是线段AB、BC、AA1的中点.
(1)判断直线C1B与平面EFG的位置关系,并说明理由;
(2)求异面直线AC1与GF所成角的大小.
高三数学教学案 第九章 立体几何
第十课时 直线与平面所成的角
考纲摘录
掌握直线与平面所成角的概念.
知识概要
7、如图,在直四棱柱ABCD-A1B1C1D1中,底面是边长为1的菱形,侧棱长为2,
(1)B1D1与A1D能否垂直?请证明你的判断.
(2)当∠A1B1C1在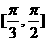 上变化时,求异面直线AC1与A1B1所成角的取值范围.
上变化时,求异面直线AC1与A1B1所成角的取值范围.

6、如图所示,空间四边形ABCD中,两条对边AB=CD=3,E、F分别是另外两条对边AD、BC上的点,且AE:ED = BF:FC=1:2,EF=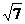 ,求AB和CD所成角的大小.
,求AB和CD所成角的大小.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com