
题目列表(包括答案和解析)
1.能够运用转化的思想化空间角为平面角;化线面间距离,面面间距离等为点到线或 线到面的距离.
2.掌握两条异面直线间的距离(只要求会计算已给出公垂线时的距离)直线和平面间的距离及两个平面间的距离的概念,并会求直线和平面间的距离,两个平面间的距离.
[教学目标]
1.掌握两条直线所成的角、直线和平面所成的角及二面角的平面角的概念,并会求
这些角.
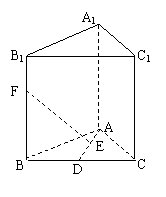
6.在正三棱柱 中,
中, 为
为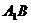 上的点,当
上的点,当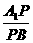 =______时,使得
=______时,使得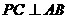 .
.
例2正方形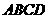 的四边
的四边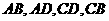 上分别取
上分别取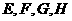 四点,使得
四点,使得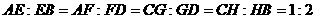 ,把正方形沿对角线
,把正方形沿对角线 折起,如图:
折起,如图:
(1)求证: 是矩形;
是矩形;
(2)当二面角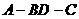 为多大时,
为多大时, 为正方形.
为正方形.
例3 在直三棱柱 中,
中,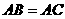 ,
,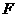 为棱BB
为棱BB 上一点,
上一点,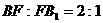 ,
, ,
, 为
为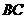 的中点.
的中点.
(1) 若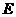 为线段
为线段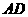 上(不同于
上(不同于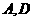 )的任意一点,求证:
)的任意一点,求证: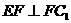 .
.
(2) 试问:若 ,在线段
,在线段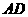 上的点
上的点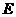 能否使
能否使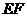 与平面
与平面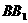
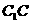 成
成 角?证明你的结论。
角?证明你的结论。
例 4在三棱锥 中,
中, 两两垂直,若
两两垂直,若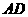 与平面
与平面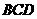 所成角为
所成角为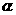 ,
,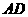 与平面
与平面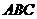 所成角为
所成角为 ,且
,且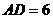 ,则当
,则当 ,
, 为何值时,三棱锥
为何值时,三棱锥 的体积最大,最大值是多少?
的体积最大,最大值是多少?
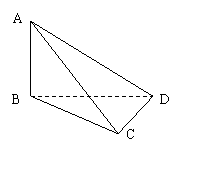
例5如图,三棱柱的底面是边长为2的等边三角形,侧面 是
是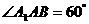 的菱形,且平面
的菱形,且平面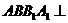 面ABC,M是
面ABC,M是 上的动点
上的动点
(1) 当M为 的中点时,求证:
的中点时,求证: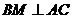
(2) 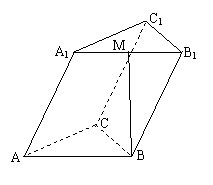 试求二面角
试求二面角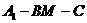 的平面角最小时,三棱锥
的平面角最小时,三棱锥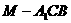 的体积
的体积
高三数学第二轮复习教学案
第十四课时 立几的综合运用
班级 学号 姓名
[教学目标]
能够解决空间角、距离及与探索问题相关的综合性问题.
[例题讲解]
例题1
(1)若二面角 为
为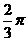 ,直线
,直线 ,则
,则 所在平面内的直线与
所在平面内的直线与 所成角的取值范围
( )
所成角的取值范围
( )
A 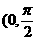 ) B
) B 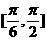 C
C  D
D 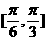
(2)在半径为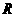 的球内有一内接正三棱锥,它的底面三个顶点恰好都在同一个大圆上,一个动点从三棱锥的一个顶点出发沿球面运动,经过其余三点后返回,则经过的最短路程是
( )
的球内有一内接正三棱锥,它的底面三个顶点恰好都在同一个大圆上,一个动点从三棱锥的一个顶点出发沿球面运动,经过其余三点后返回,则经过的最短路程是
( )
A 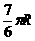 B
B  C
C 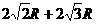 D
D 
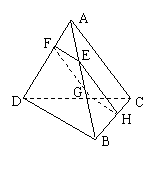
(3)正四面体ABCD的棱长为1,G是底面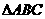 的中心,M在线段
的中心,M在线段 上且使
上且使 ,则GM的长为 ( )
,则GM的长为 ( )
A 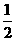 B
B 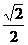 C
C  D
D 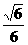
(4)在直三棱柱 中,
中, ,E,F分别为
,E,F分别为 ,
, 的中点,沿棱柱的表面从E到F两点的最短路径的长度为 ( )
的中点,沿棱柱的表面从E到F两点的最短路径的长度为 ( )
A  B
B 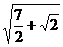 C
C 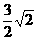 D
D
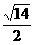
(5)正方体ABCD- 的棱长为1,在正方体表面上与点A距离是
的棱长为1,在正方体表面上与点A距离是 的点的轨迹的长度为______.
的点的轨迹的长度为______.
(6)在直角坐标系中,设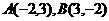 ,沿
,沿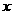 轴将直角坐标系折成
轴将直角坐标系折成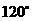 的二面角后,AB的长度是______.
的二面角后,AB的长度是______.
例2已知四棱锥 的底面为直角梯形,
的底面为直角梯形,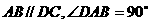 ,PA⊥底面
,PA⊥底面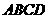 ,且
,且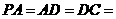
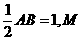 是PB的中点
是PB的中点
(1)证明:面 面
面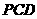
(2)求 与
与 所成的角
所成的角
(3)求面 与面
与面 所成二面角的大小
所成二面角的大小
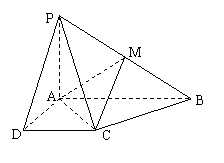
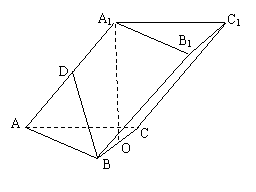
例3 斜三棱柱 中,底面是边长为
中,底面是边长为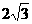 的正三角形,且点A1在底面
的正三角形,且点A1在底面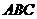 的射影O恰是BC的中点
的射影O恰是BC的中点
(1)
当侧棱 与底面成
与底面成 角时,求二面角
角时,求二面角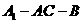 的大小
的大小
(2)
D为侧棱 上一点,当
上一点,当 为何值时,
为何值时,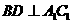
例4 如图,在长方体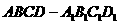 中,
中, ,点E在棱AB上移动
,点E在棱AB上移动
(1) 证明:
(2) 当E为AB的中点时,求点E到面 的距离
的距离
(3) 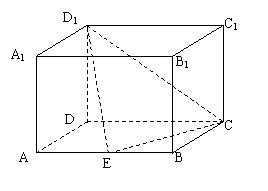 AE为何值时,二面角
AE为何值时,二面角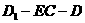 的大小为
的大小为 。
。
5.在直三棱柱 中,点
中,点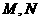 分别在
分别在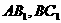 上,且
上,且
(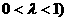 ,那么以下四个结论中正确的有_________.
,那么以下四个结论中正确的有_________.
(1)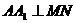 (2)
(2)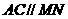 (3)
(3) 平面ABC (4)
平面ABC (4) 与
与 是异面直线
是异面直线
4.正四棱锥 的底面
的底面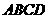 在球O的大圆面上,顶点
在球O的大圆面上,顶点 在球面上,已知球的体积为
在球面上,已知球的体积为 ,则正四棱锥
,则正四棱锥 的体积的最大值为_______.
的体积的最大值为_______.
3.在三棱柱 中,
中, 为
为 上一点,求
上一点,求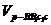 :
: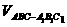 =( )
=( )
A 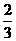 B
B 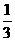 C
C  D 3
D 3
2.在侧棱长为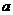 的正四棱锥中,棱锥的体积最大时,底面边长为
( )
的正四棱锥中,棱锥的体积最大时,底面边长为
( )
A 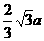 B
B  C
C 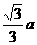 D
D 
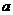
1.正方体 棱长为1,点
棱长为1,点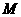 在棱
在棱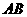 上,且
上,且 ,点
,点 是平面
是平面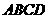 上的动点,且点P到直线
上的动点,且点P到直线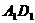 的距离与点到点
的距离与点到点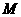 的距离的平方差为1,则点
的距离的平方差为1,则点 的轨迹是
( )
的轨迹是
( )
A 抛物线 B 双曲线 C 直线 D 椭圆
2.能够综合运用条件探索出要求的结论,或判断结论是否存在.
[例题讲解]
例题1
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com