高中数学课程内容不断发展变化，“研究性学习”进入我国基础教育课程体系，是一大亮点，对于培养具有创造精神和实践能力的开拓型人才有着重大意义.高考数学命题会要求考生通过研究性问题进行探索，抓住本质，揭示规律，勇于创新法、出新招、标新立异，以评价考生研究性学习的能力. 研究性学习的高考原创试题命题会从如下几个方面进行：

1.开放题

研究性学习逐步在数学学科中渗透，它的精髓是开放式教学，高考中的体现之一就是开放性试题，体现了数学活动的开放性和非常规化，以及活动过程中的探究性、实践性和创新性，是高考数学原创题命制的方向之一.

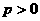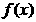典型题6：(2003年北京市高考题)若存在常数，使得函数满足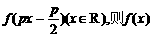的一个正周期为 　　　　　　.

注：填的正整数倍中的任何一个都正确.

人的认识是以感性认识为基础的，中学数学实验多数是重要数学公式和定理的再现，它能帮助学生形成正确的数学概念，加深对数学知识的理解，培养学生严谨的科学态度和辩证唯物主义观点.数学实验可分为观察实验、验证性实验和探索性实验，这些实验能够考查学生分析问题和解决问题的能力与创新意识，是高考原创试题的命题方向之一.

2002年高考数学文科第22题是一个剪贴实验题，分别给出了三个条件，探索相应的结论，三个问题都有不同层次的探索能力要求，大家一致公认为好题.从一个新角度来看，高考对剪拼动手操作问题的考查，大家谁都没有见过，很公平.作为素材下面提供一个数学实验题:

典型题5　 如下图：(1)圆柱面上的椭圆在圆柱侧面展开图中是什么形状?

(2)是圆弧、抛物线段等二次曲线的一部分吗?

以上问题可通过实验观察:由学生自制长方形纸片围成圆柱形，按纸片接头所在母线AB的位置分三种情形(如图1，2，3)画出截面的截口(无法精确，近似即可)，其中图3中的A，B是半圆弧的中点.观察相应展开图的形状(如图4，5，6).(结果:正弦曲线或余弦曲线!)

探求论证:建立坐标系，证明展开图中的曲线方程为的形式.

评注：此题构思新颖，又源于教材，能充分考查学生的研究性学习能力.

高考数学应用题的命题方向，是引导学生自觉地置身于现实生活的大环境中，关心身边的数学问题，了解社会，关心社会，形成健全的人格. 2004年高考应用题的背景:上海市是大学生就业问题，重庆市是过马路遇到红绿灯问题，浙江是缺电问题，真正做到了“贴近生活、背景公平、控制难度”的命题原则.随着学习能力、理性思维能力、创新意识逐步纳入高考考查的轨道，关心社会热点并结合新增内容的新颖的原创应用试题会大量出现. 下面给出两个美国案例：

典型题3　 (美国高中数学课程标准中的案例)一个学生在城市里的排球比赛中膝盖脱臼了，医生给她开了一种消炎药来消肿.她要吃10天的药，每8小时吃两片200毫克的药片.如果她的肾每8小时过滤掉60%的药，10天后还有多少药残留在她的身体中?如果她继续服用这种药一年，又会有多少药残留在她的身体中?

评注:这是一个充满人文价值和人文关怀的题目，在解决这一问题的过程中，不仅考查了学生无穷等比数列的概念，还告诉学生，药物到最后还有部分残留在体内，使学生意识到吃药在治疗伤口的同时也对身体健康有一定的副作用.引导学生注意养生之道、学会如何生存，最终形成良好的健康意识，使数学知识成了促进学生形成正确的情感态度和正确的价值观的催化剂，这是符合新课程“以人为本”的理念的.

典型题4　 (美国《Interactive Mathematics Program》高中数学教材中的案例改编)左右为难的收款方式:在一些地方送报人先买了报纸然后送到顾客家，再向顾客收取报纸的费用.

假设有一天顾客对送报人说:“不像往常一样每星期收5美元，而是随机的从这一袋中拿取2张钞票，怎么样？如果你愿意从袋中取钱的办法，从今以后每星期就采用这一方式.”

这顾客给送报人看袋子，里边有1张10美元和5张1美元的钞票.这样随机取两张钞票的总和可能是：11美元和2美元(当然顾客将会每星期用新的钞票替换上星期被抽走的钞票).请你帮送报人决策是否要采用顾客的建议：

(1)构造一个模拟的情形并用合理的数目进行检验.如，300个星期，得到11美元的机会是100次，得到2美元的机会是200次，概括这一模拟的情形，决定选择什么方法对送报人有利，并解释你的选择.

(2)用面积模型方法或其它的方法计算这一支付方式送报人的数学期望值，即采用这一支付方式从长远看送报人每星期平均得到多少美元？根据这一理论分析，确定那种方式较好，并解释你的选择.

(3)哪种方式你更觉得可靠--模拟的，还是理论分析的？为什么？

这是从实际生活问题情景出发，以数学期望为依据的决策题目，体现数学的应用价值.

经过计算，P(11)=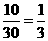， P(2)=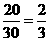，用300个星期作大数试验，结果送报人在300个星期内共得到1500美元，数学期望值是每星期5美元.说明两种方法具有同样的数学期望值.因此，两种支付方式是一样的，可以采取每星期收取5美元的方法，也可以采取从袋子中抽取钞票的方法.

数学文化是多姿多彩的，它是人类文化宝库中的奇葩.《标准》中指出：数学是人类文化的重要组成部分。数学是人类社会进步的产物，也是推动社会发展的动力。通过在高中阶段数学文化的学习，学生将初步了解数学科学与人类社会发展之间的相互作用，体会数学的科学价值、应用价值、人文价值，开阔视野，寻求数学进步的历史轨迹，激发对于数学创新原动力的认识，受到优秀文化的熏陶，领会数学的美学价值，从而提高自身的文化素养和创新意识。

《标准》强调了数学文化的重要作用，要求将其尽可能与高中数学课程内容有机结合.数学高考可能会出现考查学生数学文化的试题，如数学小作文，让学生体会数学与自然及人类社会的密切联系，了解数学的价值等，在雄厚的扎实的基础知识和基本技能基础上，进一步延伸到思想和方法、精神等文化的层次，达到一定数学文化层次的理解.

典型题2　 《红楼梦》第62回写道：“一年十二个月，月月有几个生日.人多了，就这样巧，有两个一日的，也有三个一日的.” 由此.我们引出下面的问题，请解答：

若一年按365天计，那么在当今我们随机组成的50个人的一个教学班中

(1)全班每个人的生日都不相同的概率是多少？

(2)至少有两个人生日相同的概率是多少？

(3)恰有两个人生日相同的概率是多少？

(参考数据： 365⁴⁹≈3.570×10¹²⁵， 50³⁶⁵≈1.365×10⁶²⁰， 365⁵⁰≈1.303×10¹²⁸，

)

0.(答案(1)0.03;(2)97;(3)0.1163)

在我国2003年制订的《普通高中数学课程标准》(下面简称《标准》)中，数学交流已作为一项教学目标被明确提出.使用交流去培养学生的数学理解力是数学交流的目标，但在我国高考数学中“数学交流”的试题现在基本上还没有涉及.以后会编制出不同种类的“数学交流”试题，让学生通过书面表述、图表、数学模式、数学图象、数学规律等方式进行数学交流，最终达到熟练掌握数学语言进行交流的目的.

典型题1　 (韩国高考数学题改编)下面是学生甲和学生乙争论集合的部分内容:

甲:我们能够想象到的集合之全体的集合叫做S，那么

(a)S将S自身作为元素所有，是吧?

乙:那不成体统，哪有那样的事?

甲:好，那么(b)不把自己本身作为元素的集合之全体的集合又怎么样呢?

以数学方式表达上述争论中带有底线的(a)，(b)，哪一项最好?

(A)S∈S，{A|AA，A是集合}；(B) S∈S，{A|A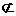A，A是集合}；

(C) S∈S，{A|AA，A是集合}；(D) SS，{A|AA，A是集合}.

评注：此题通过两个学生的数学交流来表明他们对集合与集合、集合与元素之间关系的理解，同时让应试者参与讨论，并把一些观点与数学表达符号化.

17、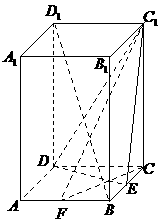

16、

15、

11、　　　　　　 　12、　　　　　　　 　、　　　　　　　 　13、　　　　　　　 　

14(1)　　　　　　 (2)　　　　　　

20．(本小题满分14分)已知函数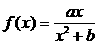在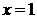处取得极值2．

(1)求函数的解析式；

(2) 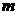满足什么条件时，区间(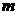，2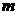+1)为函数的单调增区间；

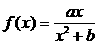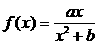(3)若为图象上任意一点，直线与的图象切于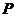点，求直线的斜率的取值范围．

高考数学综合训练(四)(四)

班级　　　　　 姓名　　　　　 座号