19.(12分)已知B(1，b)为函数f(x)=x³+ax²+1的图像上一点，过B(1，b)的切线斜率为－3.

(1)求a,b的值；

(2)若不等式f(x)≤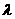－1990对于x[－1，4]恒成立，试求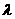的取值范围；

(3)设g(x)+f(x)=－3x²+tx+1，问： 是否存在实数t，使得当 x

(0，1]时，g(x)有最大值1？

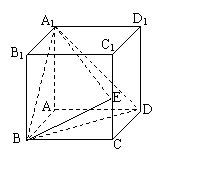
18.(12分)如图，在正方体ABCD－A₁B₁C₁D₁中，点E在棱 CC₁上.

(1)求证： A₁E⊥BD；

(2)当A₁E与面BED所成角 为多大时，面A₁BD⊥面EBD；

(3)在(2)的结论下，求此时二面角A－A₁D－E的大小.

17.(12分)袋中装着标有数字1，2，3，4，5的小球各2个，从袋中任取3个小球，按3个小球上最大数字的9倍计分，每个小球被取出的可能性都相等，用表示取出的3个小球上的最大数字.

(1)取出的3个小球上的数字互不相同的概率；

(2)随机变量的概率分布和数学期望；

(3)计分介于20分到40分之间的概率.

16.(12分)已知向量==(cos，sin)，，

其中O为坐标原点，且

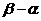(1)若求的值；

(2)若求△OAB的面积S.

15.对于实数x≥0，定义符号[x]表示不超过x的最大整数，则方程[2sinx]=[x]的解集是(x以弧度为单位)___________.

14.2006年12月1日，国内版“城市之间”南北十强决赛在海口市拉开帷幕，我省有衡阳，岳阳，郴州三市参与决赛，为满足活动的需要，海口市共准备了四个宾馆以供各代表团入住，假定每个代表团可入住任一宾馆，且入住各个宾馆是等可能的，则我省三个代表团恰好分住其中三个不同宾馆的概率为__________.

13.如图，矩形ABCD中，AB=2CD=2，且E为AB的中点，

将△ADE沿DE折起，使平面A′DE⊥平面EBCD，则A′C

与平面EBCD所成角的正切值等于__________.

12.已知实数x，y满足　　　　　　　 ，则z=x²+(y+2)²的最小值为_________.

11.若函数f(x)=　　　　　 ，则不等式xf(x)+x≤0的解集为_________.

10.已知定义域为R的函数f(x)满足f(-x)=－f(x+6)，当x＞3时，f(x)单调递增，若x₁+x₂＜6且(x₁-3)(x₂-3)＜0，则f(x₁)+f(x₂)的值(　 )

A.恒为0　　 B.恒小于 0　　 C.恒 大于0　　　 D.可正可负