
题目列表(包括答案和解析)
20.已知函数f(x)的定义域为[0,1],且同时满足:①f(1)=3;②f(x)≥2恒成立;③若x1≥0,x2≥0,x1+x2≤1,则有f(x1+x2)≥f(x1)+f(x2)-2.
(1)试求函数f(x)的最大值和最小值;
(2)试比较f(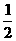 n)与
n)与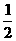 n+2的大小(n∈N);
n+2的大小(n∈N);
(3)某人发现:当x=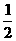 n(n∈N)时,有f(x)<2x+2.由此他提出猜想:对一切x∈(0,1],都有f(x)<2x+2,请你判断此猜想是否正确,并说明理由.
n(n∈N)时,有f(x)<2x+2.由此他提出猜想:对一切x∈(0,1],都有f(x)<2x+2,请你判断此猜想是否正确,并说明理由.
19.如图,公园有一块边长为2a的等边△ABC的边角地,现修成草坪,图中DE把草坪分成面积相等的两部分,D在AB上,E在AC上.
(1)设AD=x(x≥0),ED=y,求用x表示y的函数关系式;
(2)如果DE是灌溉水管,为节约成本,希望它最短,DE的位置应在哪里?如果DE是参观线路,则希望它最长,DE的位置又应在哪里?请予证明.

18.已知函数y=f(x)满足f(x)=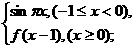
(1)分别写出x∈[0,1)时y=f(x)的解析式f1(x)和x∈[1,2)时y=f(x)的解析式f2(x);并猜想x∈[n,n+1],n≥-1,n∈Z时y=f(x)的解析式f n+1(x)(用x和n表示)(不必证明);
(2)当x=n+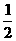 (n≥-1,n∈Z)时,y=f n+1(x)x∈[n,n+1),(n≥-1,n∈Z)的图象上有点列A n+1(x,f(x))和点列B n+1(n+1,f(n+1)),线段A n+1B n+2与线段B n+1A
n+2的交点C n+1,求点C n+1的坐标(a n+1(x),b n+1(x));
(n≥-1,n∈Z)时,y=f n+1(x)x∈[n,n+1),(n≥-1,n∈Z)的图象上有点列A n+1(x,f(x))和点列B n+1(n+1,f(n+1)),线段A n+1B n+2与线段B n+1A
n+2的交点C n+1,求点C n+1的坐标(a n+1(x),b n+1(x));
(3)在前面(1)(2)的基础上,请你提出一个点列C n+1(a n+1(x),b n+1(x))的问题,并进行研究,并写下你研究的过程.
17.某花木场存放装满泥土的花盆,每堆最底层(第一层)摆放呈长20只,宽14只的矩形,上面各层均比它的下一层长宽各少一只.已知每只装满泥土的花盆的重量为2kg,为使堆放稳定,每两层之间放有一块耐压的轻质薄板(重量忽略不计).每只花盆的最大抗压力为8kg,所有花盆不破碎、不变形
 .
.
(1)求第n层(自下而上,下同)摆放多少只花盆?
(2)问这堆花盆能否摆7层?如果能,求出第7层的花盆数;如果不能,说明理由,并求这堆花盆最多可摆多少只.
16.某公司为了帮助尚有26.8万元无息贷款没有偿还的残疾人商店,借出20万元将该商店改建成经营状况良好的某种消费品专卖店,并约定用该店经营的利润逐步偿还债务(不计息).已知:该种消费品的进价为每件40元;该店每月销售量q(百件)与销售价p(元/件)的关系用图中的一条折线表示;职工每人每月工资为600元,该店应交付的其他费用为每月13 200元.

(1)如果当销售价p为52元/件时,该店正好收支平衡,求该店的职工人数;
(2)如果该店只安排40名职工,则该店最早可在几年后还清所有债务,此时每件消费品价定为多少元?
15.甲、乙、丙三个口袋内都分别装有6个不相同的球,并且每个口袋内的6个球均有1个红球,2个黑球,3个无色透明的球,现从甲、乙、丙三个口袋中依次随机各摸出1个球.
理科:(1)求恰好摸出红球、黑球和无色球各
1个的概率;
(2)求摸出的3个球中含有有色球数ξ的概率分布列和数学期望.
文科:(1)求恰好摸出2个黑球的概率;
(2)求恰好摸出红球、黑球和无色透明球各1个的概率;
(3)求摸出的3个球中至少有1个是有色球的概率.
14.在△ABC中,O为中线AM上的一个动点,若AM=2,则 (
(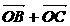 )的最小值是_________.
)的最小值是_________.
13.把实数a,b,c,d排形成如 的形式,称之为二行二列矩阵.定义矩阵的一种运算
的形式,称之为二行二列矩阵.定义矩阵的一种运算 ·
· ,该运算的几何意义为平面上的点(x,y)在矩阵
,该运算的几何意义为平面上的点(x,y)在矩阵 的作用下变换成点(ax+by,cx+dy),则点(2,3)在矩阵
的作用下变换成点(ax+by,cx+dy),则点(2,3)在矩阵 的作用下变换成点_________.又若曲线x2+4xy+2y2=1在矩阵
的作用下变换成点_________.又若曲线x2+4xy+2y2=1在矩阵 的作用下变换成曲线x2-2y2=1,则a+b的值为____________.
的作用下变换成曲线x2-2y2=1,则a+b的值为____________.
12.2005年10月,我国载人航天飞船“神六”飞行获得圆满成功.已知“神六”飞船变轨前的运行轨道是一个以地心为焦点的椭圆,飞船近地点、远地点离地面的距离分别为200公里、250公里.设地球半径为R公里,则此时飞船轨道的离心率为_________.(结果用R的式子表示)
11.(理)一个总体中有100个个体,随机编号0,1,2,…,99,依编号顺序平均分成10个小组,组号依次为1,2,3,…,10.现用系统抽样方法抽取一个容量为10的样本,规定如果在第1组随机抽取的号码为m,那么在第k组中抽取的号码个位数字与m+k的个位数字相同,若m=6,则在第7组中抽取的号码是_________.
(文)一个公司共有280个员工,下设一些部门,要采用分层抽样方法从全体员工中抽取一个容量为40的样本,如果从某个部门的所有员工抽取的员工人数是5,那么这个部门的员工人数为_____________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com