
题目列表(包括答案和解析)
2.已知b≠0,则b=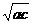 是a、b、c成等比数列的
是a、b、c成等比数列的
A.充分不必要条件 B.必要不充分条件
C.充要条件? D.既不充分又不必要条件
1.设某等差数列的首项为a(a≠0),第二项为b.则这个数列中有一项为0的充要条件是
A.a-b是正整数 B.a+b是正整数
C.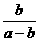 D.
D. 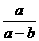 是正整数
是正整数
19.A有一个放有x个红球、y个白球、z个黄球的箱子(x、y、z≥1,x+y+z=6),B有一个放有3个红球、2个白球、1个黄球的箱子,两人各自从自己的箱子中任取一球,规定当两球同色时为A胜,异色时为B胜.
(1)用x、y、z表示A胜的概率;
(2)若又规定当A取红、白、黄而得胜的得分分别为1、2、3;负则得0分,求使A得分的期望最大的x、y、z.
18.一出租车司机从饭店到火车站途中有6个交通岗,假设他在各交通岗遇到红灯这一事件是相互独立的,并且概率都是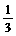 .
.
(1)求这位司机遇到红灯前,已经通过了2个交通岗的概率;
(2)求这位司机在途中遇到红灯数ξ的期望和方差.
17.某先生居住在城镇的A处,准备开车到单位B处上班.若该地各路段发生堵车事件都是相互独立的,且在同一路段发生堵车事件最多只有一次,发生堵车事件的概率如图所示(例如A→C→D算作两个路段:路段AC发生堵车事件的概率为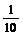 ,路段CD发生堵车事件的概率为
,路段CD发生堵车事件的概率为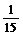 ).
).
(1)请你为其选择一条由A到B的路线,使得途中发生堵车事件的概率最小;
(2)若记路线A→C→F→B中遇到堵车次数为随机变量ξ,求ξ的数学期望Eξ.
|
16.某市出租车的起步价为6元,行驶路程不超过3km时,租车费为6元,若行驶路程超过3km,则按每超出1km(不足1km也按1km计程)收费3元计费.
设出租车一天行驶的路程数ξ(按整km数计算,不足1km的自动计为1km)是一个随机变量,则其收费也是一个随机变量.已知一个司机在某个月每次出车都超过了3 km,且一天的总路程数可能的取值是200、220、240、260、280、300(km),它们出现的概率依次是0.12、0.18、0.20、0.20、100a2+3a、4a.
(1)求这一个月中一天行驶路程ξ的分布列,并求ξ的数学期望和方差.
(2)求这一个月中一天所收租车费η的数学期望和方差.
15.某篮球队与其他6支篮球队依次进行6场比赛,每场均决出胜负,设这支篮球队与其他篮球队比赛胜场的事件是独立的,并且胜场的概率是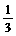 .
.
(1)求这支篮球队首次胜场前已经负了两场的概率;
(2)求这支篮球队在6场比赛中恰好胜了3场的概率;
(3)求这支篮球队在6场比赛中胜场数的期望和方差.
14.罐中有6个红球,4个白球,从中任取1球,记住颜色后再放回,连续摸取4次,设ξ为取得红球的次数,则ξ的期望Eξ= .
13.某人有6把钥匙,其中只有一把能打开门,今任取一把试开,不能打开的除去,则打开此门所需试开次数ξ的数学期望Eξ= .
12.两名战士在一次射击比赛中,战士甲得1分、2分、3分的概率分别为0.4、0.1、0.5;战士乙得1分、2分、3分的概率分别为0.1、0.6、0.3,那么两名战士得胜希望大的是 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com