12.某些植物发芽具有这样一种规律：当年所发新芽第二年不发芽，老芽在以后每年都发芽，如下表(设第一年前的新芽数为a)：

照这样下去，第8年老芽数与总芽数的比值为　　　　　　　 　(精确到0.001).

11.在n行m列的方格表中每个方格上都填上一个数，使得第n行的m个数与每列的n个数分别都成等差数列，如果表的角上的四个数的和等于s，则这个表中所有数的和等于　　　　　　　　　　　　 .

10.已知数列{a_n}的前n项和S_n=，则数列{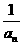}的前n项和T_n=　　　　　 .

9.在等比数列{a_n}中，a₁+a₂+a₃= -3，a₁·a₂·a₃=8，且a₁>a₃，则a_n=　　　　　　 .　

8.某人从2002年1月1日起，且以后每年1月1日到银行存入a元(一年定期)，若年利

率r保持不变，且每年到期后存款均自动转为新一年定期，到2008年1月1日将所有存款及利息全部取回，他可取回的钱数(单位为元)为

?A.a(1+r)⁷　　　　　　　　　 B. ［(1+r)⁷-(1+r)］

?C.a(1+r)⁸　　　　　　　　　 D. ［(1+r)⁸-(1+r)］

第Ⅱ卷(非选择题，共60分)　

7.下列四个图形中，着色三角形的个数依次构成一个数列的前4项，则这个数列的一个通项公式为　

A. a_n=3^n-1?　　 B.a_n=3ⁿ　　　　　 C.a_n=3ⁿ -2n　　　　 D.a_n=3^n-1+2n-3

6.等比数列{a_n}中，a₁=512，公比q=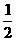，用Π_n表示它的前n项之积：Π_n=a₁·a₂·…·a_n，则Π₁，Π₂…中最大的是

?A.Π₁₂?　　 ?B.Π₁₁?　　 ?C.Π₉　　　　　　 ?D.Π₈　

5. 已知a_n=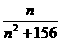 (n∈N^*)，则数列{a_n}的最大项为

?A.a₁₂?　　　 ?B.a₁₃?　　　 ?C.a₁₂或a₁₃?　　　 ?D.不存在　

4.若数列{a_n}的通项公式为a_n=5()^2n-2 -4()^n-1(n∈N^*)，{a_n}的最大项为第x项，最小项为第y项，则x+y等于

?A.3　　　　　　 B.4　　　　　　 C.5　　　　　　　　 D.6

3.已知等差数列{a_n}的前n项和为S_n，且S₂=10，S₅=55，则过点P(n，)，Q(n+2，)(n∈N^*)的一次函数解析式是

A.y=2x+1　　　 B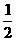.y=　　　　　　　 C.y=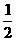x-1　　 ?D.y=2x-1