
题目列表(包括答案和解析)
8.曲线y=x (n∈N)在点P(
(n∈N)在点P(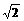 ,2
,2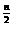 )处切线斜率为20,那么n为 ( )
)处切线斜率为20,那么n为 ( )
A.7 B.6 C.5 D.4
7.一圆面以10π cm /s的速率增加,那么当圆半径r=20 cm 时,其半径r的增加速率u为 ( )
/s的速率增加,那么当圆半径r=20 cm 时,其半径r的增加速率u为 ( )
A.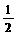 cm/s
B.
cm/s
B. cm/s
C.
cm/s
C. cm/s
D.
cm/s
D.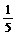 cm/s
cm/s
6.一个圆半径以0.1 cm/s速率增加,那么当半径r=10 cm时,此圆面积的增加速率(单位:cm /s)为
( )
/s)为
( )
A.3π B.4π C.2π D.π
5.一质点做直线运动,若它所经过的路程与时间的关系为:s(t)=4t -3(s单位:m,t单位:s),则t=5时的瞬时速率为 ( )
-3(s单位:m,t单位:s),则t=5时的瞬时速率为 ( )
A.37 B.38 C.39 D.40
4.已知过曲线y= x
x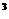 上点P的切线l的方程为12x-3y=16,那么P点坐标只能为 ( )
上点P的切线l的方程为12x-3y=16,那么P点坐标只能为 ( )
A. B.
B.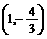 C.
C. D.
D.
3.物体自由落体运动方程为s=s(t)=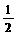 gt
gt ,g=9.8m/s
,g=9.8m/s ,若v=
,若v=
 =g=9.8m/s.那么下列说法正确的是 ( )
=g=9.8m/s.那么下列说法正确的是 ( )
A.9.8m/s是在1s这段时间内的速率
B.9.8m/s是从1s到(1+Δt)s这段时间内的速率
C.9.8m/s是物体在t=1 s这一时刻的速率
D.9.8m/s是物体从1 s到(1+Δt)s这段时间内的平均速率
2.过原点与曲线y= 相切的切线方程为
( )
相切的切线方程为
( )
A.y=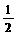 x
B.y=2x C.y=x
D.y=
x
B.y=2x C.y=x
D.y= x
x
1.曲线y=x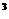 在点P(2,8)处的切线方程为 ( )
在点P(2,8)处的切线方程为 ( )
A.y=6x-12 B.y=12x-16 C.y=8x+10 D.y=12x-32
19. 我们想像着给白球编号,于是有白1,白2,白3,白4,白5,白6,白7共7个白球;又想像着给黑球编号,有黑1,黑2,黑3共3个黑球.
从这十个不同的球中,任意取出两个球的取法共有 =45种.每一种取法就是一个基本事件.由于这些球大小相同,我们认为取得白1和白2的可能性与取得黑1和黑2的可能性是相等的.这就是说,这45种取法中,每两种的可能性都是相等的.这样就得到一个含有45个基本事件的等可能基本事件集.这样来假设等可能性就合乎情理了.
=45种.每一种取法就是一个基本事件.由于这些球大小相同,我们认为取得白1和白2的可能性与取得黑1和黑2的可能性是相等的.这就是说,这45种取法中,每两种的可能性都是相等的.这样就得到一个含有45个基本事件的等可能基本事件集.这样来假设等可能性就合乎情理了.
取得一个黑球和白球的取法共有多少呢?根据分步计数原理,共有 3=21种取法.
3=21种取法.
∴P(摸得一个白球和一个黑球)= .
.
18.(1)设没有人排除为事件A,1个人排队为事件B,2个人排队为事件C,则P(A)=0.1, P(B)=0.16, P(C)=0.3,依题意A、B、C彼此互斥,所以至多2个人排队的概率为:
P(A+B+C)=P(A)+P(B)+P(C)=0.1+0.16+0.3=0.56.
(2)设至少2个人排队为事件D,则 为至多1个人排队,即
为至多1个人排队,即 =A+B,因此
=A+B,因此
P(D)=1-P( )=1-P(A+B)=1-[P(A)+P(B)]=1-(0.1+0.16)=0.74.
)=1-P(A+B)=1-[P(A)+P(B)]=1-(0.1+0.16)=0.74.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com