
题目列表(包括答案和解析)
3.(石庄中学) 已知正项数{an}满足a1= a (0<a<1) ,且
 ,求证:
,求证:
(I)  ; (II)
; (II)
 .
.
解析:(I) 将条件 变形,得
变形,得 .
.
于是,有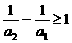 ,
, ,
, ,……
,…… .
.
将这n-1个不等式叠加,得 ,故
,故 .
.
(II) 注意到0<a<1,于是由(I)得 =
=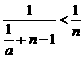 ,
,
从而,有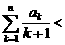

 .
.
2.(如中)已知一个等比数列 前四项之积为
前四项之积为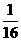 ,第二、三项的和为
,第二、三项的和为 ,求这个等比数列的公比.
,求这个等比数列的公比.
[错解] 四个数成等比数列,可设其分别为
四个数成等比数列,可设其分别为
则有 ,解得
,解得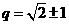 或
或 ,
,
故原数列的公比为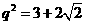 或
或
[错解分析]按上述设法,等比数列公比 ,各项一定同号,而原题中无此条件
,各项一定同号,而原题中无此条件
[正解]设四个数分别为
则 ,
,

由 时,可得
时,可得
当 时,可得
时,可得
1.(如中)设数列的前 项和为
项和为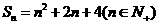 ,求这个数列的通项公公式
,求这个数列的通项公公式
[错解] 
[错解分析]此题错在没有分析 的情况,以偏概全.误认为任何情况下都有
的情况,以偏概全.误认为任何情况下都有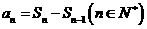
[正解] 
因此数列的通项公式是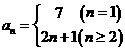
24.(案中)若数列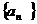 为等差数列且
为等差数列且 ,则数列
,则数列 ,类比上述性质,相应地若数列
,类比上述性质,相应地若数列 >0,
>0, ,则有
,则有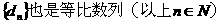
正确答案:
错误原因:类比意识不强
23.(案中)若an=1+2+3+…+n,则数列 的前n项之和
的前n项之和 =
。
=
。
正确答案:
错误原因:未能将an先求和得 不强。
不强。
22.(案中)数列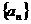 的前n项之和为
的前n项之和为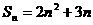 ,若将此数列按如下规律编组:(
,若将此数列按如下规律编组:( )、(
)、( ,
,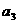 )、(
)、( ,
, ,
,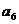 )、……,则第n组的n个数之和为
。
)、……,则第n组的n个数之和为
。
正确答案:
错误原因:未能明确第n组各项的构成规律,尤其是首项和最后一项,从而找不到合适的解法,应转化为: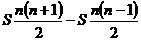
21.(薛中)对任意正整数n,  满足数列是递增数列,则
满足数列是递增数列,则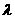 的取值范围是
。
的取值范围是
。
答案: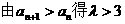
错解:
错因:利用二次函数的对称轴,忽视其与 的关系。
的关系。
20.(薛中)已知数列 是非零等差数列,又a1,a3,a9组成一个等比数列的前三项,则
是非零等差数列,又a1,a3,a9组成一个等比数列的前三项,则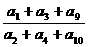 的值是
。
的值是
。
答案:1或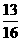
错解: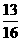
错因:忘考虑公差为零的情况。
19.(薛中)若 ,则数列
,则数列 的前n项和Sn=
。
的前n项和Sn=
。
答案: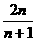
错解:
错因:裂项求和时系数2丢掉。
18.(丁中)等差数列{an}中, a1=25, S17= ,则该数列的前__________项之和最大,其最大值为_______。
,则该数列的前__________项之和最大,其最大值为_______。
错解:12
错因:忽视
正解:12或13 , 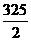
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com