
题目列表(包括答案和解析)
3、已知0<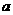 <1,
<1, <-1,则函数
<-1,则函数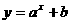 的图象必定不经过( )
的图象必定不经过( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
2、已知函数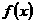 的定义域为[0,1],值域为[1,2],则函数
的定义域为[0,1],值域为[1,2],则函数 的定义域和值域分别是( )
的定义域和值域分别是( )
A. [0,1] ,[1,2] B. [2,3] ,[3,4] C. [-2,-1] ,[1,2] D. [-1,2] ,[3,4]
1、已知函数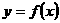 ,
, ,那么集合
,那么集合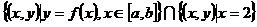 中元素的个数为( )
中元素的个数为( )
A. 1 B. 0 C. 1或0 D. 1或2
8.(一中)已知向量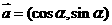 ,
,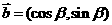 ,
,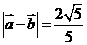 .
.
(Ⅰ)求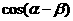 的值;
的值;
(Ⅱ)若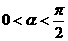 ,
,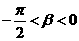 ,且
,且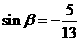 ,求
,求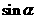 的值.
的值.
解(Ⅰ)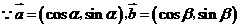 ,
,
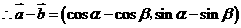 .
.
 ,
,  ,
,
即 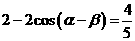 .
. 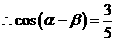 .
.
(Ⅱ)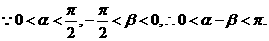
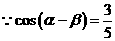 ,
,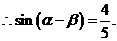
 ,
,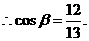
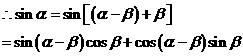
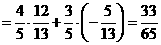 .
.
欢迎访问
7.(磨中)已知a=(cosα,sinα),b=(cosβ,sinβ),a与b之间有关系|ka+b|= |a-kb|,其中k>0,
|a-kb|,其中k>0,
(1)用k表示a·b;
(2)求a·b的最小值,并求此时a·b的夹角的大小。
解 (1)要求用k表示a·b,而已知|ka+b|= |a-kb|,故采用两边平方,得
|a-kb|,故采用两边平方,得
|ka+b|2=( |a-kb|)2
|a-kb|)2
k2a2+b2+2ka·b=3(a2+k2b2-2ka·b)
∴8k·a·b=(3-k2)a2+(3k2-1)b2
a·b =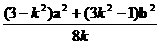
∵a=(cosα,sinα),b=(cosβ,sinβ),
∴a2=1, b2=1,
∴a·b =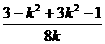 =
=
(2)∵k2+1≥2k,即 ≥
≥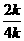 =
=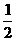
∴a·b的最小值为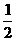 ,
,
又∵a·b =| a|·|b |·cos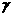 ,|a|=|b|=1
,|a|=|b|=1
∴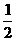 =1×1×cos
=1×1×cos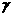 。
。
∴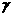 =60°,此时a与b的夹角为60°。
=60°,此时a与b的夹角为60°。
错误原因:向量运算不够熟练。实际上与代数运算相同,有时可以在含有向量的式子左右两边平方,且有|a+b|2=|(a+b)2|=a2+b2+2a·b或|a|2+|b|2+2a·b。
6.(石庄中学)已知向量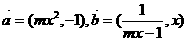 (m为常数),且
(m为常数),且 ,
,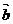 不共线,若向量
不共线,若向量 ,
,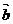 的夹角落<
的夹角落< ,
, 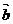 >为锐角,求实数x的取值范围.
>为锐角,求实数x的取值范围.
解:要满足< >为锐角
>为锐角
只须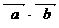 >0且
>0且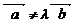 (
(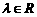 )
)
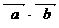 =
=
= 
=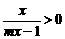
即 x (mx-1) >0
1°当 m > 0时
x<0
或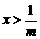
2°m<0时
x ( -mx+1) <0
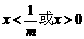
3°m=0时 只要x<0
综上所述:x > 0时,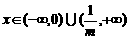
x = 0时,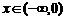
x < 0时,
5.(石庄中学)已知ÐA、ÐB、ÐC为DABC的内角,且f(A、B)=sin22A+cos22B-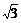 sin2A-cos2B+2
sin2A-cos2B+2
(1)当f(A、B)取最小值时,求ÐC
(2)当A+B= 时,将函数f(A、B)按向量
时,将函数f(A、B)按向量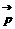 平移后得到函数f(A)=2cos2A求
平移后得到函数f(A)=2cos2A求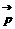
解:(1) f(A、B)=(sin22A-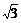 sin2A+
sin2A+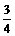 )+(cos22B-cos2B+
)+(cos22B-cos2B+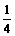 )+1
)+1
=(sin2A-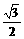 )2+(sin2B-
)2+(sin2B- )2+1
)2+1
当sin2A=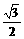 ,sin2B=
,sin2B= 时取得最小值,
时取得最小值,
∴A=30°或60°,2B=60°或120° C=180°-B-A=120°或90°
(2) f(A、B)=sin22A+cos22(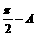 )-
)-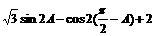
=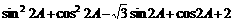
=
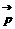 =
=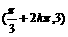
4.(石庄中学)已知函数f(x)=m|x-1|(mÎR且m¹0)设向量 ),
), ,
,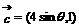 ,
, ,当qÎ(0,
,当qÎ(0,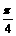 )时,比较f(
)时,比较f(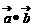 )与f(
)与f( )的大小。
)的大小。
解: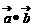 =2+cos2q,
=2+cos2q, =2sin2q+1=2-cos2q
=2sin2q+1=2-cos2q
f(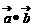 )=m|1+cos2q|=2mcos2q
)=m|1+cos2q|=2mcos2q
f( )=m|1-cos2q|=2msin2q
)=m|1-cos2q|=2msin2q
于是有f(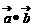 )-f(
)-f( )=2m(cos2q-sin2q)=2mcos2q
)=2m(cos2q-sin2q)=2mcos2q
∵qÎ(0,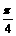 ) ∴2qÎ(0,
) ∴2qÎ(0,  ) ∴cos2q>0
) ∴cos2q>0
∴当m>0时,2mcos2q>0,即f(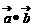 )>f(
)>f( )
)
当m<0时,2mcos2q<0,即f(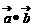 )<f(
)<f( )
)
3.(石庄中学)已知向量m=(1,1),向量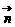 与向量
与向量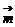 夹角为
夹角为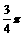 ,且
,且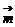 ·
·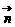 =-1,
=-1,
(1)求向量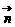 ;
;
(2)若向量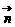 与向量
与向量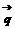 =(1,0)的夹角为
=(1,0)的夹角为 ,向量
,向量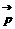 =(cosA,2cos2
=(cosA,2cos2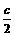 ),其中A、C为DABC的内角,且A、B、C依次成等差数列,试求|
),其中A、C为DABC的内角,且A、B、C依次成等差数列,试求|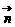 +
+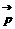 |的取值范围。
|的取值范围。
解:(1)设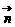 =(x,y)
=(x,y)
则由<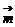 ,
,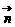 >=
>=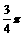 得:cos<
得:cos<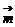 ,
,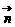 >=
>= =
=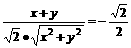 ①
①
由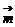 ·
·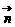 =-1得x+y=-1 ②
=-1得x+y=-1 ②
联立①②两式得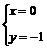 或
或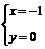
∴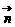 =(0,-1)或(-1,0)
=(0,-1)或(-1,0)
(2) ∵<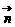 ,
,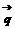 >=
>=
得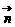 ·
·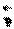 =0
=0
若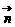 =(1,0)则
=(1,0)则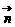 ·
·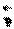 =-1¹0
=-1¹0
故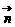 ¹(-1,0) ∴
¹(-1,0) ∴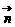 =(0,-1)
=(0,-1)
∵2B=A+C,A+B+C=p
ÞB=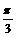 ∴C=
∴C=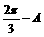
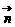 +
+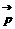 =(cosA,2cos2
=(cosA,2cos2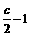 )
)
=(cosA,cosC)
∴|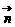 +
+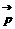 |=
|=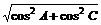 =
=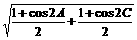 =
=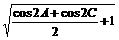
=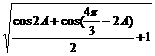
=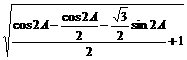
=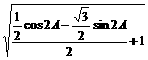
=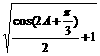
∵0<A<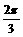
∴0<2A<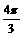
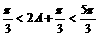
∴-1<cos(2A+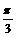 )<
)<
∴|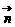 +
+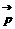 |Î(
|Î(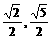 )
)
2.(如中)在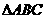 中,已知
中,已知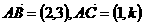 ,且
,且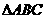 的一个内角为直角,求实数
的一个内角为直角,求实数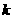 的值.
的值.
错误分析:是自以为是,凭直觉认为某个角度是直角,而忽视对诸情况的讨论.
答案: (1)若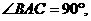 即
即
故 ,从而
,从而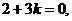 解得
解得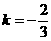 ;
;
(2)若 即
即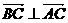 ,也就是
,也就是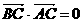 ,而
,而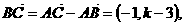 故
故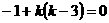 ,解得
,解得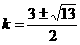 ;
;
(3)若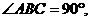 即
即 ,也就是
,也就是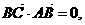 而
而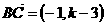 ,故
,故 ,解得
,解得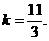
综合上面讨论可知,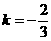 或
或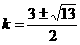 或
或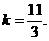
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com