
题目列表(包括答案和解析)
1. 方程sin2x=sinx在区间(0,2π)内解的个数是_____。
A. 1 B. 2 C. 3 D. 4
8. 建造一个容积为8m ,深为2m的长方体无盖水池,如果池底和池壁的造价每平方米分别为120元和80元,则水池的最低造价为___________。
,深为2m的长方体无盖水池,如果池底和池壁的造价每平方米分别为120元和80元,则水池的最低造价为___________。
Ⅱ、示范性题组:
例1. 设a>0,a≠1,试求方程log (x-ak)=log
(x-ak)=log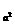 (x
(x -a
-a )有实数解的k的范围。(89年全国高考)
)有实数解的k的范围。(89年全国高考)
[解] 将原方程化为:log (x-ak)=log
(x-ak)=log
 , 等价于
, 等价于  (a>0,a≠1)
(a>0,a≠1)
∴ k= -
- ( |
( | |>1 ),
|>1 ),
设 =cscθ, θ∈(-
=cscθ, θ∈(-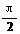 ,0)∪(0,
,0)∪(0, 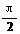 ),则 k=f(θ)=cscθ-|ctgθ|
),则 k=f(θ)=cscθ-|ctgθ|
当θ∈(-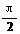 ,0)时,f(θ)=cscθ+ctgθ=ctg
,0)时,f(θ)=cscθ+ctgθ=ctg <-1,故k<-1;
<-1,故k<-1;
当θ∈(0,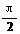 )时,f(θ)=…
)时,f(θ)=…
综上,k的取值范围是…
[注] 引入新的变量,而用函数值域加以分析,此法可解有关不等式、方程、最值、参数范围之类问题。(分离参数法、三角换元法、等价转化思想)
[另解] (数形结合法):
[再解] (方程讨论法):
例2. 设不等式2x-1>m(x -1)对满足|m|≤2的一切实数m的取值都成立。求x的取值范围。
-1)对满足|m|≤2的一切实数m的取值都成立。求x的取值范围。
[分析] 此问题由于常见的思维定势,易把它看成关于x的不等式讨论。然而,若变换一个角度以m为变量,记f(m)=(x -1)m-(2x-1),则问题转化为求一次函数(或常数函数)f(m)的值在[-2,2]内恒负时参数x应满足的条件。
-1)m-(2x-1),则问题转化为求一次函数(或常数函数)f(m)的值在[-2,2]内恒负时参数x应满足的条件。
[解] 设f(m)=(x -1)m-(2x-1), 则
-1)m-(2x-1), 则 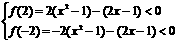
解得x∈(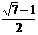 ,
,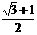 )
)
[注] 本题有别于关于x的不等式2x-1>m(x -1)的解集是[-2,2]时求m的值、关于x的不等式2x-1>m(x
-1)的解集是[-2,2]时求m的值、关于x的不等式2x-1>m(x -1)在[-2,2]上恒成立时求m的范围。
-1)在[-2,2]上恒成立时求m的范围。
在一个含有多个变量的数学问题中,确定合适的变量和参数,从而揭示函数关系,使问题更明朗化。
例3. 设等差数列{a }的前n项的和为S
}的前n项的和为S ,已知a
,已知a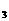 =12,S
=12,S >0,S
>0,S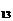 <0 。
<0 。
①.求公差d的取值范围; ②.指出S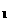 、S
、S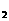 、…、S
、…、S 中哪一个值最大,并说明理由。(92年全国高考)
中哪一个值最大,并说明理由。(92年全国高考)
[分析] ①问用a 、S
、S 易求;②问利用S
易求;②问利用S 是n的二次函数而求什么时候取最大值。
是n的二次函数而求什么时候取最大值。
[解]
[注] 数列的通项公式及前n项和公式实质上是定义在自然数集上的函数,因此可利用函数思想来分析或用函数方法来解决数列问题。
[另解②问](寻求a >0、a
>0、a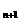 <0 ):
<0 ):
例4. 如图,AB是圆O的直径,PA垂直于圆O所在平面,C是圆周上任一点,设∠BAC=θ,PA=AB=2r,求异面直线PB和AC的距离。
[分析] 异面直线PB和AC的距离可看成求直线PB上任意一点到AC的距离的最小值,从而设定变量,建立目标函数而求函数最小值。
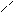        P
M
A
H B
D C P
M
A
H B
D C |
[解] 在PB上任取一点M,作MD⊥AC于D,MH⊥AB于H,
设MH=x,则MH⊥平面ABC,AC⊥HD 。
∴MD =x
=x +[(2r-x)sinθ]
+[(2r-x)sinθ] =(sin
=(sin +1)x
+1)x -4rsin
-4rsin θx+4r
θx+4r sin
sin θ
θ
=(sin θ+1)[x-
θ+1)[x-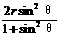 ]
] +
+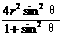
即当x=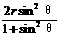 时,MD取最小值
时,MD取最小值 为两异面直线的距离。
为两异面直线的距离。
[注] 求最大值、最小值的实际问题,将文字说明转化成数学语言后,建立数学模型和函数关系式,利用函数性质、重要不等式和有关知识解答。(见再现性题组第8题)
例5. 已知△ABC三内角A、B、C的大小成等差数列,且tgA·tgC=2+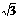 ,又知顶点C的对边c上的高等于4
,又知顶点C的对边c上的高等于4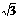 ,求△ABC的三边a、b、c及三内角。
,求△ABC的三边a、b、c及三内角。
[解] 由A、B、C成等差数列,可得B=60°;
由△ABC中tgA+tgB+tgC=tgA·tgB·tgC,得tgA+tgC=tgB(tgA·tgC-1)=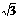 (1+
(1+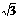 )
)
设tgA、tgC是方程x -(
-(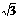 +3)x+2+
+3)x+2+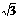 =0的两根,解得x
=0的两根,解得x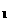 =1,x
=1,x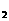 =2+
=2+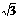
设A<C,则tgA=1,tgC=2+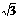 , ∴A=
, ∴A= ,C=
,C=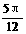
…
例6. 若(z-x) -4(x-y)(y-z)=0,求证:x、y、z成等差数列。
-4(x-y)(y-z)=0,求证:x、y、z成等差数列。
[分析] 题设正好是判别式b -4ac=0的形式,因此构造一个一元二次方程求解。
-4ac=0的形式,因此构造一个一元二次方程求解。
[证明] 当x=y时,可得x=z, ∴x、y、z成等差数列;
当x≠y时,设方程(x-y)t -(z-x)t+(y-z)=0,由△=0得t
-(z-x)t+(y-z)=0,由△=0得t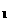 =t
=t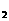 ,并易知t=1是方程的根。
,并易知t=1是方程的根。
∴t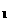 ·t
·t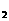 =
=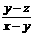 =1 , 即2y=x+z , ∴x、y、z成等差数列
=1 , 即2y=x+z , ∴x、y、z成等差数列
[注] 题设条件具备或经变形整理后具备x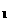 +x
+x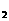 =a、x
=a、x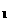 ·x
·x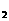 =b的形式,则利用根与系数的关系构造方程;具备b
=b的形式,则利用根与系数的关系构造方程;具备b -4ac≥0或b
-4ac≥0或b -4ac≤0的形式,可利用根的判别式构造一元二次方程。
-4ac≤0的形式,可利用根的判别式构造一元二次方程。
例7. △ABC中,求证:cosA·cosB·cosC≤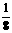 。
。
[证明] 设k=cosA·cosB·cosC=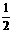 [cos(A+B)+cos(A-B)]·cosC=
[cos(A+B)+cos(A-B)]·cosC=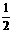 [-cosC+cos(A-B)]cosC
[-cosC+cos(A-B)]cosC
整理得:cos C-cos(A-B)·cosC+2k=0,即看作关于cosC的一元二次方程。
C-cos(A-B)·cosC+2k=0,即看作关于cosC的一元二次方程。
∴ △=cos (A-B)-8k≥0 即 8k≤cos
(A-B)-8k≥0 即 8k≤cos (A-B)≤1 ∴ k≤
(A-B)≤1 ∴ k≤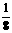 即cosA·cosB·cosC≤
即cosA·cosB·cosC≤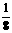
[注]既是方程思想,也属判别式法。还可用放缩法:cosA·cosB·cosC=… =
-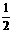 cos
cos C+
C+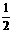 cos(A-B)·cosC=-
cos(A-B)·cosC=-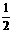 [cosC-
[cosC-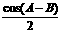 ]
] +
+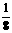 cos
cos (A-B)≤
(A-B)≤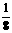 cos
cos (A-B) ≤
(A-B) ≤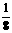
例8. 设f(x)=lg ,如果当x∈(-∞,1]时f(x)有意义,求实数a的取值范围。
,如果当x∈(-∞,1]时f(x)有意义,求实数a的取值范围。
[解] 由题可知,不等式1+2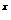 +4
+4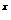 a>0在x∈(-∞,1]上恒成立,即:(
a>0在x∈(-∞,1]上恒成立,即:(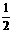 )
) +(
+(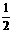 )
)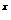 +a>0
+a>0
设t=(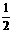 )
)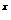 , 则t≥
, 则t≥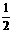 , 又设g(t)=t
, 又设g(t)=t +t+a,其对称轴为t=-
+t+a,其对称轴为t=-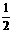
∴ t +t+a=0在[
+t+a=0在[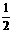 ,+∞)上无实根, 即 g(
,+∞)上无实根, 即 g(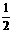 )=(
)=(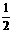 )
) +
+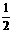 +a>0,得a>-
+a>0,得a>-
[注] 二次函数及图像、二次不等式、二次方程三者是紧密联系的。也可用分离参数法:
Ⅲ、巩固性题组:
7.正六棱锥的体积为48,侧面与底面所成的角为45°,则此棱锥的侧面积为___________。
6.关于x的方程sin x+cosx+a=0有实根,则实数a的取值范围是__________。
x+cosx+a=0有实根,则实数a的取值范围是__________。
5. 已知等差数列的前n项和为S ,且S
,且S =S
=S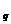 (p≠q,p、q∈N),则S
(p≠q,p、q∈N),则S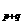 =_________。
=_________。
4. 已知sinθ+cosθ=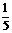 ,θ∈(
,θ∈(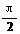 ,π),则tgθ的值是_____。
,π),则tgθ的值是_____。
A. -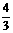 B. -
B. - C.
C. 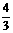 D.
D. 
3. 已知函数y=f(x)有反函数,则方程f(x)=a (a是常数) ______。
A.有且仅有一个实根 B.至多一个实根 C.至少一个实根 D.不同于以上结论
2. 如果函数f(x)=x +bx+c对于任意实数t,都有f(2+t)=f(2-t),那么_____。
+bx+c对于任意实数t,都有f(2+t)=f(2-t),那么_____。
A. f(2)<f(1)<f(4) B. f(1)<f(2)<f(4) C. f(2)<f(4)<f(1) D. f(4)<f(2)<f(1)
函数思想,是指用函数的概念和性质去分析问题、转化问题和解决问题。方程思想,是从问题的数量关系入手,运用数学语言将问题中的条件转化为数学模型(方程、不等式、或方程与不等式的混合组),然后通过解方程(组)或不等式(组)来使问题获解。有时,还实现函数与方程的互相转化、接轨,达到解决问题的目的。
Ⅰ、再现性题组:
1. 方程lgx+x=3的解所在的区间为_____。
A. (0,1) B. (1,2) C. (2,3) D. (3,+∞)
14.
函数f(x)=(|m|-1)x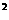 -2(m+1)x-1的图像与x轴只有一个公共点,求参数m的值及交点坐标。
-2(m+1)x-1的图像与x轴只有一个公共点,求参数m的值及交点坐标。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com