
题目列表(包括答案和解析)
1、设集合 ,集合
,集合 ,那么
,那么 ( )
( )
(A) (B)
(B)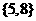 (C)
(C)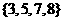 (D)
(D)
解析:选A.
(17)(本小题满分12分)
厂家在产品出厂前,需对产品做检验,厂家对一般产品致冷商家的,商家符合规定拾取一定数量的产品做检验,以决定是否验收这些产品.
(Ⅰ)若厂家库房中的每件产品合格的概率为0.3,从中任意取出4种进行检验,求至少要1件是合格产品的概率.
(Ⅱ)若厂家发给商家20件产品,其中有3件不合格,按合同规定该商家从中任取2件,来进行检验,只有2件产品合格时才接收这些产品,否则拒收,分别求出该商家计算出不合格产品为1件和2件的概率,并求该商家拒收这些产品的概率。
(18)(本小题满分12分)
已知cosα= ,cos(α-β)=
,cos(α-β)= ,且0<β<α<
,且0<β<α<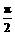 ,
,
(Ⅰ)求tan2α的值;
(Ⅱ)求β.
(19) (本小题满分12分)
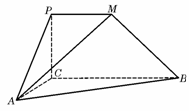 如图,平面PCBM⊥平面ABC,∠PCB=90°,PM∥BC,直线AM与直线PC所成的角为60°,又AC=1,BC=2PM=2,∠ACB=90°
如图,平面PCBM⊥平面ABC,∠PCB=90°,PM∥BC,直线AM与直线PC所成的角为60°,又AC=1,BC=2PM=2,∠ACB=90°
(Ⅰ)求证:AC⊥BM;
(Ⅱ)求二面角M-AB-C的大小;
(Ⅲ)求多面体PMABC的体积.
(20)(本小题满分12分)
设函数f(x)=ax3+bx+c(a≠0)为奇函数,其图象在点(1,f(1))处的切线与直线x-6y-7=0垂直,导函数f'(x)的最小值为-12.
(Ⅰ)求a,b,c的值;
(Ⅱ)求函数f(x)的单调递增区间,并求函数f(x)在(-1,3)上的最大值和最小值.
(21)(本小题满分12分)
求F1、F2分别是横线 的左、右焦点.
的左、右焦点.
(Ⅰ)若r是第一象限内该数轴上的一点,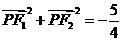 ,求点P的作标;
,求点P的作标;
(Ⅱ)设过定点M(0,2)的直线l与椭圆交于同的两点A、B,且∠ADB为锐角(其中O为作标原点),求直线 的斜率
的斜率 的取值范围.
的取值范围.
(22)(本小题满分14分)
已知函数f(x)=x2-4,设曲线y=f(x)在点(xn,f(xn))处的切线与x轴的交点为(xn+1,u)(u,N +),其中为正实数.
(Ⅰ)用xx表示xn+1;
(Ⅱ)若a1=4,记an=lg ,证明数列{a1}成等比数列,并求数列{xn}的通项公式;
,证明数列{a1}成等比数列,并求数列{xn}的通项公式;
(Ⅲ)若x1=4,bn=xn-2,Tn是数列{bn}的前n项和,证明Tn<3.
(含详细解析)
(13). 的展开式中的第5项为常数项,那么正整数
的展开式中的第5项为常数项,那么正整数 的值是
.
的值是
.
(1)设集合M={4,5,6,8},集合N={3,5,7,8}那么M∪N=
(A){3,4,5,6,7,8} (B){5,8} (C){3,5,7,8} (D){4,5,6,8}
 (2)函数f(x)=1+log2x与g(x)=2-x+1在同一直角坐标系下的图象大致是
(2)函数f(x)=1+log2x与g(x)=2-x+1在同一直角坐标系下的图象大致是
 (3)某商场买来一车苹果,从中随机抽取了10个苹果,其重量(单位:克)分别为:150,152,153,
(3)某商场买来一车苹果,从中随机抽取了10个苹果,其重量(单位:克)分别为:150,152,153,
149,148,146,151,150,152,147,由此估计这车苹果单个重量的期望值是
(A)150.2克 (B)149.8克 (C)149.4克 (D)147.8克
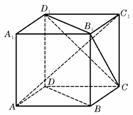
(4)如图,ABCD-A1B1C1D1为正方体,下面结论错误的是
(A)BD∥平面CB1D1 (B)AC1⊥BD
(C)AC1⊥平面CB1D1 (D)异面直线AD与CB所成的角为60°
(5)如果双曲线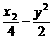 =1上一点P到双曲线右焦点的距离是2,那么点P到y轴的距离是
=1上一点P到双曲线右焦点的距离是2,那么点P到y轴的距离是
 (A)
(A) (B)
(B) (C)
(C)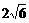 (D)
(D)
(6)设球O的半径是1,A、B、C是球面上三点,已知A到B、C两点的
球面距离都是 ,且二面角B-OA-C的大小是
,且二面角B-OA-C的大小是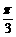 ,则从A点沿球面经B、C
,则从A点沿球面经B、C
两点再回到A点的最短距离是
(A) (B)
(B) (C)
(C)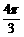 (D)
(D)
(7)等差数列{an}中,a1=1,a3+a5=14,其降n项和Sn=100,则n=
(A)9 (B)10 (C)11 (D)12
(8)设A(a,1),B(2,b),C(4,5)为坐标平面上三点,O为坐标原点,若OA与OB在OC方向上的投影相同,则a与b满足的关系式为
A.4a-5b=3 B.5a-4b=3 C.4a+5b=14 D.5a+4b=12
(9)用数字1,2,3,4,5可以组成没有重复数字,并且比20 000大的五位偶数共有
A.48个 B.36个 C.24个 D.18个
(10)已知抛物线y-x2+3上存在关于直线x+y=0对称的相异两点A、B,则|AB|等于
A.3
B.4 C.3 D.4
D.4
(11)某公司有60万元资金,计划投资甲、乙两个项目,按要求对项目甲的投资不小于对项目乙投资的 倍,且对每个项目的投资不能低于5万元,对项目甲每投资1万元可获得0.4万元的利润,对项目乙每投资1万元可获得0.6万元的利润,该公司正确提财投资后,在两个项目上共可获得的最大利润为
倍,且对每个项目的投资不能低于5万元,对项目甲每投资1万元可获得0.4万元的利润,对项目乙每投资1万元可获得0.6万元的利润,该公司正确提财投资后,在两个项目上共可获得的最大利润为
 A.36万元
B.31.2万元 C.30.4万元 D.24万元
A.36万元
B.31.2万元 C.30.4万元 D.24万元
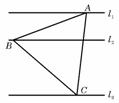
(12)如图,l1、l2、l3是同一平面内的三条平行直线,l1与l2与l3同的距离是2,
正三角形ABC的三顶点分别在l1、l2、l3上,则△ABC的边长是
A.2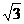 B.
B. C.
C.  D.
D.
(17)(本小题满分12分)已知 <
< <
< <
< ,
,
(Ⅰ)求 的值.
的值.
(Ⅱ)求 .
.
(18)(本小题满分12分)厂家在产品出厂前,需对产品做检验,厂家将一批产品发给商家时,商家按合同规定也需随机抽取一定数量的产品做检验,以决定是否接收这批产品.
(Ⅰ)若厂家库房中的每件产品合格的概率为0.8,从中任意取出4件进行检验.求至少有1件是合格品的概率;
(Ⅱ)若厂家发给商家20件产品,其中有3件不合格,按合同规定该商家从中任取2件,都进行检验,只有2件都合格时才接收这批产品,否则拒收.求该商家可能检验出不合格产品数 的分布列及期望
的分布列及期望 ,并求该商家拒收这批产品的概率.
,并求该商家拒收这批产品的概率.
 (19)(本小题满分12分)如图,
(19)(本小题满分12分)如图, 是直角梯形,∠
是直角梯形,∠ =90°,
=90°,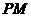 ∥
∥ ,
,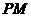 =1,
=1, =2,又
=2,又 =1,∠
=1,∠ =120°,
=120°, ⊥
⊥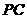 ,直线
,直线 与直线
与直线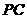 所成的角为60°.
所成的角为60°.
(Ⅰ)求证:平面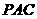 ⊥平面
⊥平面 ;
;
(Ⅱ)求二面角 的大小;
的大小;
(Ⅲ)求三棱锥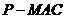 的体积.
的体积.
(20)(本小题满分12分)设 、
、 分别是椭圆
分别是椭圆 的左、右焦点.
的左、右焦点.
(Ⅰ)若 是该椭圆上的一个动点,求
是该椭圆上的一个动点,求 ·
· 的最大值和最小值;
的最大值和最小值;
(Ⅱ)设过定点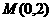 的直线
的直线 与椭圆交于不同的两点
与椭圆交于不同的两点 、
、 ,且∠
,且∠ 为锐角(其中
为锐角(其中 为坐标原点),求直线
为坐标原点),求直线 的斜率
的斜率 的取值范围.
的取值范围.
已知函数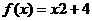 ,设曲线
,设曲线 在点()处的切线与x轴线发点()()其中xn为实数
在点()处的切线与x轴线发点()()其中xn为实数
(21)(本小题满分12分)
(22)(本小题满分14分)
设函数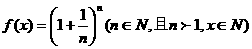 .
.
(Ⅰ)当x=6时,求 的展开式中二项式系数最大的项;
的展开式中二项式系数最大的项;
(Ⅱ)对任意的实数x,证明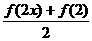 >
>
(Ⅲ)是否存在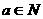 ,使得an<
,使得an< <
< 恒成立?若存在,试证明你的结论并求出a的值;若不存在,请说明理由.
恒成立?若存在,试证明你的结论并求出a的值;若不存在,请说明理由.
 (13)若函数f(x)=e-(m-u)2
(c是自然对数的底数)的最大值是m,且f(x)是偶函数,则m+u= .
(13)若函数f(x)=e-(m-u)2
(c是自然对数的底数)的最大值是m,且f(x)是偶函数,则m+u= .
(14)如图,在正三棱柱ABC-A1B1C1中,侧棱长为 ,底面三角形的边长为1,
,底面三角形的边长为1,
则BC1与侧面ACC1A1所成的角是 .
(15)已知⊙O的方程是x2+y2-2=0, ⊙O’的方程是x2+y2-8x+10=0,由动点P向⊙O和
⊙O’所引的切线长相等,则动点P的轨迹方程是 .
(16)下面有五个命题:
①函数y=sin4x-cos4x的最小正周期是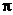 .
.
②终边在y轴上的角的集合是{a|a= |.
|.
③在同一坐标系中,函数y=sinx的图象和函数y=x的图象有三个公共点.
④把函数
⑤函数
其中真命题的序号是 (写出所言 )
(1)复数 的值是
的值是
(A)0 (B)1 (C)-1 (D)1
(2)函数f(x)=1+log2x与g(x)=2-x+1在同一直角坐标系下的图象大致是

 (3)
(3)
(A)0
(B)1
(C)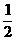 (D)
(D)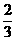
(4)如图,ABCD-A1B1C1D1为正方体,下面结论错误的是
(A)BD∥平面CB1D1 (B)AC1⊥BD
(C)AC1⊥平面CB1D1 (D)异面直线AD与CB1角为60°
(5)如果双曲线 上一点P到双曲线右焦点的距离是2,那么点P到y轴的距离是
上一点P到双曲线右焦点的距离是2,那么点P到y轴的距离是
(A) (B)
(B) (C)
(C) (D)
(D)
(6)设球O的半径是1,A、B、C是球面上三点,已知A到B、C两点的球面距离都是 ,且
,且
 三面角B-OA-C的大小为
三面角B-OA-C的大小为 ,则从A点沿球面经B、C两点再回到A点的最短距离是
,则从A点沿球面经B、C两点再回到A点的最短距离是
(A) (B)
(B)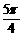 (C)
(C) (D)
(D)
(7)设A{a,1},B{2,b},C{4,5},为坐标平面上三点,O为坐标原点,若
 上的投影相同,则a与b满足的关系式为
上的投影相同,则a与b满足的关系式为
(A)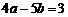 (B)
(B)
(C)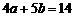 (D)
(D)
(8)已知抛物线 上存在关于直线
上存在关于直线 对称的相异两点A、B,则|AB|等于
对称的相异两点A、B,则|AB|等于
(A)3 (B)4 (C)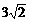 (D)
(D)
(9)某公司有60万元资金,计划投资甲、乙两个项目,按要求对项目甲的投资不小于对项目乙投资的 倍,且对每个项目的投资不能低于5万元,对项目甲每投资1万元可获得0.4万元的利润,对项目乙每投资1万元可获得0.6万元的利润,该公司正确规划投资后,在这两个项目上共可获得的最大利润为
倍,且对每个项目的投资不能低于5万元,对项目甲每投资1万元可获得0.4万元的利润,对项目乙每投资1万元可获得0.6万元的利润,该公司正确规划投资后,在这两个项目上共可获得的最大利润为
(A)36万元 (B)31.2万元 (C)30.4万元 (D)24万元
(10)用数字0,1,2,3,4,5可以组成没有重复数字,并且比20000大的五位偶数共有
 (A)288个 (B)240个 (C)144个 (D)126个
(A)288个 (B)240个 (C)144个 (D)126个
(11)如图,l1、l2、l3是同一平面内的三条平行直线,l1与l2间的距离是1,
l2与l3间的距离是2,正三角形ABC的三顶点分别在l1、l2、l3上,
则△ABC的边长是
(A) (B)
(B) (C)
(C) (D)
(D)
(12)已知一组抛物线 ,其中a为2,4,6,8中任取的一个数,b为1,3,5,7中任取的一个数,从这些抛物线中任意抽取两条,它们在与直线x=1交点处的切线相互平行的概率是
,其中a为2,4,6,8中任取的一个数,b为1,3,5,7中任取的一个数,从这些抛物线中任意抽取两条,它们在与直线x=1交点处的切线相互平行的概率是
(A) (B)
(B) (C)
(C) (D)
(D)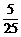
例1.作出下列函数的图象(1)y=|x-2|(x+1);
解:(1)当x≥2时,即x-2≥0时,
当x<2时,即x-2<0时,

这是分段函数,每段函数图象可根据二次函数图象作出(见图6)
例2.
解析:

 ,
,

例3.(福建卷)已知 是二次函数,不等式
是二次函数,不等式 的解集是
的解集是 且
且 在区间
在区间 上的最大值是12。 (I)求
上的最大值是12。 (I)求 的解析式; (II)是否存在实数
的解析式; (II)是否存在实数 使得方程
使得方程 在区间
在区间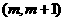 内有且只有两个不等的实数根?若存在,求出
内有且只有两个不等的实数根?若存在,求出 的取值范围;若不存在,说明理由。
的取值范围;若不存在,说明理由。
解:(I)
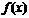 是二次函数,且
是二次函数,且 的解集是
的解集是
 可设
可设
 在区间
在区间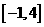 上的最大值是
上的最大值是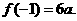
由已知,得
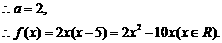
(II)方程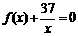 等价于方程
等价于方程
设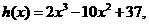 则
则
当 时,
时,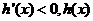 是减函数;当
是减函数;当 时,
时, 是增函数。
是增函数。 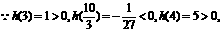
 方程
方程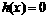 在区间
在区间 内分别有惟一实数根,而在区间
内分别有惟一实数根,而在区间
 内没有实数根,所以存在惟一的自然数
内没有实数根,所以存在惟一的自然数 使得方程
使得方程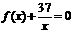 在区间
在区间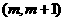 内有且只有两个不同的实数根。
内有且只有两个不同的实数根。
例4:已知二次函数f(x)=ax2+bx+c和一次函数g(x)=-bx,其中a、b、c满足a>b>c,a+b+c=0,(a,b,c∈R) (1)求证
(1)求证 两函数的图象交于不同的两点A、B; (2)求线段AB在x轴上的射影A1B1的长的取值范围
两函数的图象交于不同的两点A、B; (2)求线段AB在x轴上的射影A1B1的长的取值范围
解: (1)证明 由
由 消去y得ax2+2bx+c=0
消去y得ax2+2bx+c=0
Δ=4b2-4ac=4(-a-c)2-4ac=4(a2+ac+c2)=4[(a+ c2]
c2]
∵a+b+c=0,a>b>c,∴a>0,c<0 ∴ c2>0,∴Δ>0,即两函数的图象交于不同的两点
c2>0,∴Δ>0,即两函数的图象交于不同的两点
(2)解 设方程ax2+bx+c=0的两根为x1和x2,则x1+x2=-
设方程ax2+bx+c=0的两根为x1和x2,则x1+x2=- ,x1x2=
,x1x2=

|A1B1|2=(x1-x2)2=(x1+x2)2-4x1x2
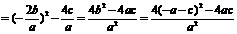

∵a>b>c,a+b+c=0,a>0,c<0,∴a>-a-c>c,解得 ∈(-2,-
∈(-2,- )
)
∵ 的对称轴方程是
的对称轴方程是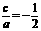

 ∈(-2,-
∈(-2,-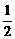 )时,为减函数
)时,为减函数
∴|A1B1|2∈(3,12),故|A1B1|∈( )
)
例5:已知f(x)=x2+c,且f[f(x)]=f(x2+1) (1)设g(x)=f[f(x)],求g(x)的解析式;(2)设φ(x)=g(x)-λf(x),试问 是否存在实数λ,使φ(x)在(-∞,-1)内为减函数,且在(-1,0)内是增函数
是否存在实数λ,使φ(x)在(-∞,-1)内为减函数,且在(-1,0)内是增函数
点拨与提示:由f[f(x)]=f(x2+1)求出c,进而得到函数的解析式,利用导数研究函数的单调性.
解: (1)由题意得f[f(x)]=f(x2+c)=(x2+c)2+c, f(x2+1)=(x2+1)2+c,∵f[f(x)]=f(x2+1)
∴(x2+c)2+c=(x2+1)2+c,∴x2+c=x2+1,∴c=1 ∴f(x)=x2+1,g(x)=f[f(x)]=f(x2+1)=(x2+1)2+1
(2)φ(x)=g(x)-λf(x)=x4+(2-λ)x2+(2-λ)
若满足条件的λ存在,则φ′(x)=4x3+2(2-λ)x
∵函数φ(x)在(-∞,-1)上是减函数, ∴当x<-1时,φ′(x)<0
即4x3+2(2-λ)x<0对于x∈(-∞,-1)恒成立
∴2(2-λ)>-4x2, ∵x<-1,∴-4x2<-4 ∴2(2-λ)≥-4,解得λ≤4
又函数φ(x)在(-1,0)上是增函数 ∴当-1<x<0时,φ′(x)>0
即4x2+2(2-λ)x>0对于x∈(-1,0)恒成立
∴2(2-λ)<-4x2, ∵-1<x<0,∴-4<4x2<0 ∴2(2-λ)≤-4,解得λ≥4
故当λ=4时,φ(x)在(-∞,-1)上是减函数,在(-1,0)上是增函数,即满足条件的λ存在
例6. 已知 ,t∈[
,t∈[ ,8],对于f(t)值域内的所有实数m,不等式
,8],对于f(t)值域内的所有实数m,不等式 恒成立,求x的取值范围。
恒成立,求x的取值范围。
解:∵t∈[ ,8],∴f(t)∈[
,8],∴f(t)∈[ ,3]原题转化为:
,3]原题转化为: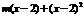 >0恒成立,为m的一次函数(这里思维的转化很重要)当x=2时,不等式不成立。∴x≠2。令g(m)=
>0恒成立,为m的一次函数(这里思维的转化很重要)当x=2时,不等式不成立。∴x≠2。令g(m)=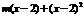 ,m∈[
,m∈[ ,3]问题转化为g(m)在m∈[
,3]问题转化为g(m)在m∈[ ,3]上恒对于0,则:
,3]上恒对于0,则: ;解得:x>2或x<-1
;解得:x>2或x<-1
例8. (见备考指南148页例3)
(见备考指南148页例3)
解:


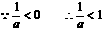



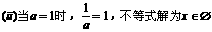
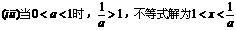
综上所述,得原不等式的解集为

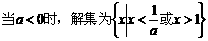 ;
; ;
;
 ;
; ;
;
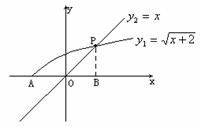
例9. 若方程 上有唯一解,
上有唯一解,
求m的取值范围。
解:原方程等价于
令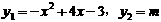 ,在同一坐标系内,画出它们的图象,
,在同一坐标系内,画出它们的图象,
其中注意 ,当且仅当两函数的图象在[0,3)上有唯一公共点时,原方程有唯一解,由下图可见,当m=1,或
,当且仅当两函数的图象在[0,3)上有唯一公共点时,原方程有唯一解,由下图可见,当m=1,或 时,原方程有唯一解,因此m的取值范围为[-3,0]
时,原方程有唯一解,因此m的取值范围为[-3,0] {1}。
{1}。
例10.设函数f(x)=ax2+bx+c的图象与两直线y=x,y= x,均不相交.试证明对一切
x,均不相交.试证明对一切 都有
都有 .
.
证明:由题意知,a≠0.设f(x)=a(x-x0)2+f(x0),则
又二次方程ax2+bx+c=±x无实根,故 Δ1=(b+1)2-4ac<0,Δ2=(b-1)2-4ac<0.
所以(b+1)2+(b-1)2-8ac<0,即2b2+2-8ac<0,即b2-4ac<-1,所以|b2-4ac|>1.


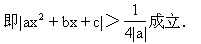
15.设函数f(x)=x2+mx+n,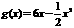 若不等式
若不等式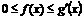 的解集为{x|2≤x≤3或x=6},求m,n的值.
的解集为{x|2≤x≤3或x=6},求m,n的值.
14.已知 为常数,若
为常数,若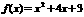 ,
,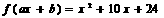 ,则
,则 = 2 。
= 2 。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com