
题目列表(包括答案和解析)
3.证明三角不等式的方法:比较法、配方法、反证法、分析法,利用函数的单调性,利用正、余弦函数的有界性,利用单位圆三角函数线及判别法等。
2.证明三角等式的思路和方法。
(1)思路:利用三角公式进行化名,化角,改变运算结构,使等式两边化为同一形式。
(2)证明方法:综合法、分析法、比较法、代换法、相消法、数学归纳法。
1.三角函数恒等变形的基本策略。
(1)常值代换:特别是用“1”的代换,如1=cos2θ+sin2θ=tanx·cotx=tan45°等。
(2)项的分拆与角的配凑。如分拆项:sin2x+2cos2x=(sin2x+cos2x)+cos2x=1+cos2x;配凑角:α=(α+β)-β,β= -
- 等。
等。
(3)降次与升次。(4)化弦(切)法。
(4)引入辅助角。asinθ+bcosθ= sin(θ+
sin(θ+ ),这里辅助角
),这里辅助角 所在象限由a、b的符号确定,
所在象限由a、b的符号确定, 角的值由tan
角的值由tan =
= 确定。
确定。
2004年各地高考中本部分所占分值在17-22分,主要以选择题和解答题的形式出现。主要考察内容按综合难度分,我认为有以下几个层次:
第一层次:通过诱导公式和倍角公式的简单运用,解决有关三角函数基本性质的问题。如判断符号、求值、求周期、判断奇偶性等。
第二层次:三角函数公式变形中的某些常用技巧的运用。如辅助角公式、平方公式逆用、切弦互化等。
第三层次:充分利用三角函数作为一种特殊函数的图象及周期性、奇偶性、单调性、有界性等特殊性质,解决较复杂的函数问题。如分段函数值,求复合函数值域等。
2.熟练掌握正弦函数、余弦函数、正切函数、余切函数的性质,并能用它研究复合函数的性质;熟练掌握正弦函数、余弦函数、正切函数、余切函数图象的形状、特点,并会用五点画出函数 的图象;理解图象平移变换、伸缩变换的意义,并会用这两种变换研究函数图象的变化.
的图象;理解图象平移变换、伸缩变换的意义,并会用这两种变换研究函数图象的变化.
1.熟练掌握三角变换的所有公式,理解每个公式的意义,应用特点,常规使用方法等;熟悉三角变换常用的方法--化弦法,降幂法,角的变换法等;并能应用这些方法进行三角函数式的求值、化简、证明;掌握三角变换公式在三角形中应用的特点,并能结合三角形的公式解决一些实际问题.
20、求角的方法:先确定角的范围,再求出关于此角的某一个三角函数(要注意选择,其标准有二:一是此三角函数在角的范围内具有单调性;二是根据条件易求出此三角函数值)。
10.反三角函数:
(1)反三角函数的定义(以反正弦函数为例): 表示一个角,这个角的正弦值为
表示一个角,这个角的正弦值为 ,且这个角在
,且这个角在 内
内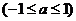 。
。
(2)反正弦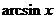 、反余弦
、反余弦 、反正切
、反正切 的取值范围分别是
的取值范围分别是 .
.
9.研究函数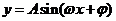 性质的方法:类比于研究
性质的方法:类比于研究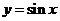 的性质,只需将
的性质,只需将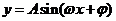 中的
中的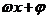 看成
看成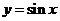 中的
中的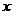 ,但在求
,但在求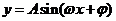 的单调区间时,要特别注意A和
的单调区间时,要特别注意A和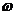 的符号,通过诱导公式先将
的符号,通过诱导公式先将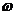 化正。
化正。
8、形如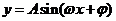 的函数:
的函数:
(1)几个物理量:A―振幅; ―频率(周期的倒数);
―频率(周期的倒数);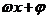 ―相位;
―相位;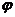 ―初相;
―初相;
(2)函数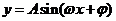 表达式的确定:A由最值确定;
表达式的确定:A由最值确定;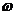 由周期确定;
由周期确定;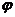 由图象上的特殊点确定,
由图象上的特殊点确定,
(3)函数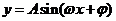 图象的画法:①“五点法”――设
图象的画法:①“五点法”――设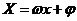 ,令
,令 =0,
=0, 求出相应的
求出相应的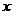 值,计算得出五点的坐标,描点后得出图象;②图象变换法:这是作函数简图常用方法。
值,计算得出五点的坐标,描点后得出图象;②图象变换法:这是作函数简图常用方法。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com