
题目列表(包括答案和解析)
1. 已知函数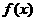 的定义域是
的定义域是 ,当
,当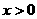 时,
时,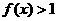 ,且
,且
(1)求 ; (2)证明:
; (2)证明: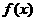 在定义域上是增函数.
在定义域上是增函数.
2. 山东卷和海南卷,在选择填空题对于新课标新增内容以中等难度的题目出现,体现了新课程的理念。
[典型例题]
例1:求函数
 的单调区间。
的单调区间。
解:略.
分析:这是一类双曲线型的特殊函数,有对称中心,对称轴,渐近线。可对以上的例题进行推广变形。
(1)求函数 的单调区间.
的单调区间.
(2)求函数
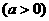 的单调区间.
的单调区间.
(3)求函数
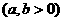 的单调区间.
的单调区间.
(4)求函数 的单调区间.
的单调区间.
(5)证明 在
在 上是增函数.
上是增函数.
例2:对于函数

(1)讨论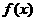 的奇偶性;(2)讨论
的奇偶性;(2)讨论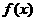 的单调性;(3)求此函数的值域.
的单调性;(3)求此函数的值域.
解:略.
例3:已知函数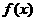 的定义域是
的定义域是 ,当
,当 时,
时,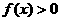 ,且
,且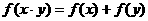
(1)求 ;
(2)证明:
;
(2)证明: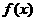 在定义域上是增函数.
在定义域上是增函数.
解:略。
分析:利用抽象函数的任意性,取特殊值进行求解。判断抽象函数的单调性,要注意掌握一些变形的技巧。可以进行推广。
9. 函数与方程:
(1)理解函数的零点和方程的根的关系、根的存在性定理,了解单调函数零点唯一性的判定。
(2)结合函数的图像,能够用二分法求相应方程的近似解,并注重这种思想方法的应用.
III.导数及其应用
[考纲要求]
(1)导数概念及其几何意义
① 了解导数概念的实际背景.
② 理解导数的几何意义.
(2)导数的运算
① 能根据导数定义,求函数 的导数.
的导数.
② 能利用表1给出的基本初等函数的导数公式和导数的四则运算法则求简单函数的导数,能求简单的复合函数(仅限于形如f(ax+b))的导数.
表1:常见基本初等函数的导数公式和常用导数运算公式:
 (C为常数);
(C为常数); , n∈N+;
, n∈N+; ;
;
 ;
;  ;
;  ;
; 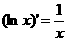 ;
;  .
.
法则1  .
.
法则2  .
.
法则3  .
.
(3)导数在研究函数中的应用
① 了解函数单调性和导数的关系;能利用导数研究函数的单调性,会求函数的单调区间(对多项式函数一般不超过三次).
②了解函数在某点取得极值的必要条件和充分条件;会用导数求函数的极大值、极小值(对多项式函数一般不超过三次);会求闭区间上函数的最大值、最小值(对多项式函数一般不超过三次).
(4)生活中的优化问题:会利用导数解决某些实际问题.
(5)定积分与微积分基本定理
① 了解定积分的实际背景,了解定积分的基本思想,了解定积分的概念.
② 了解微积分基本定理的含义.
[07年考纲与06年考纲的比较]
|
07考纲(新) |
06考纲(旧) |
|
理解导数的几何意义. |
掌握函数在一点处的导数的定义和导数的几何意义 |
|
能求简单的复合函数(仅限于形如f(ax+b))的导数. |
了解复合函数的求导法则,会求某些简单函数的导数. |
|
了解函数在某点取得极值的必要条件和充分条件;会用导数求函数的极大值、极小值,对多项式函数一般不超过三次;会求闭区间上函数的最大值、最小值,对多项式函数一般不超过三次. |
了解可导函数在某点取得极值的必要条件和充分条件(导数在极值点两侧异号);会求一些实际问题(一般指单峰函数)的最大值和最小值. |
|
定积分与微积分基本定理,推理与证明 |
|
[目标定位]
(1)了解导数概念的某些实际背景(如瞬时速度、加速度、光滑曲线切线的斜率等),掌握函数在一点处的导数的定义和导数的几何意义,理解导函数的概念.
(2)熟记基本求导公式(C,xm(m为有理数),sinx,cosx,ex,ax,lnx,logax的导数),掌握两个函数和、差、积、商的求导法则.了解复合函数的求导法则,会求某些简单函数的导数.
(3)了解可导函数的单调性与其导数的关系,了解可导函数在某点取得极值的必要条件和充分条件(导数在极值点两侧异号),会求一些实际问题(一般指单峰函数)的最大值和最小值.
[新增内容]:定积分与微积分基本定理
微积分基本定理是高等数学的基础,在高中数学中要求较低,目标层次为了解,只要求学生能根据微积分基本定理求一些较为简单的定积分,能利用定积分的几何意义求面积.
[课时建议] 8课时.
[重点与难点]
(1) 利用求导公式、运算法则求导函数。
(2) 重视利用导数定义和几何意义解题,导函数的几何意义是过曲线上点作曲线切线的斜率,导函数的代数意义是其符号可以判断函数的单调性。
(3) 理解利用导数研究函数的单调性和极值.
(4) 导数的应用
(5) 会求简单函数的定积分.
[07年新课程地区高考试卷统计分析]
|
知识点 |
题型 |
广东 |
山东 |
宁夏海南 |
|
|
含有全称命题的否定 |
选择 |
|
√ |
√ |
|
|
对数函数的定义域、集合运算 |
选择 |
√ |
|
|
|
|
指数不等式、集合运算 |
选择 |
|
√ |
|
|
|
函数的图象 |
选择 |
√ |
|
|
|
|
幂函数、函数奇偶性 |
选择 |
|
√ |
|
|
|
充要条件 |
选择 |
|
√ |
|
|
|
过曲线上点的切线所围成的面积 |
选择 |
|
|
√ |
|
|
已知函数奇偶性求参数 |
填空 |
|
|
√ |
|
|
对数函数图象的定点、基本不等式 |
填空 |
|
√ |
|
|
|
二次函数的零点 |
解答 |
√ |
|
|
|
|
以自然对数为背景的极值等问题 |
解答 |
|
√ |
√ |
|
|
以二次函数、二次方程的根、导数为背景的数列问题 |
解答 |
√ |
|
|
|
|
集合、运算信息题 |
选择 |
√ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8. 函数图象及变换: 函数图象的平移变换和对称变换。
7. 基本初等函数,加强应用以及数形结合思想.
6. 函数的奇偶性
(1)掌握函数的奇偶性的定义及图象特征,并能判断和证明函数的奇偶性,理解奇偶性是对函数的一种分类.
(2)求对称区间的解析式,并能利用函数的对称性进行画函数图像以及判断.
(3)利用函数的奇偶性解决问题.
(4)注意0在定义域内是,奇函数有 ;偶函数 的灵活应用。
5. 函数的单调性
(1)能用函数单调性的定义证明函数的单调性.
(2)求复合函数的单调区间.
(3)比较大小.
(4)利用函数单调性求值域,最值,并理解最值的含义与几何意义.
(5)解不等式.
(6)利用函数的单调性解决问题.
4. 函数值域:课标要求比原教材有所降低,建议不要追求深度、难度。重点解决以下几种题型的值域问题。
(1)一次函数值域:定义域为R和给定区间.
(2)二次函数值域:定义域为R和给定区间,可适当补充含参讨论求最值,例如区间定、轴不定和轴定、区间不定的最值问题。
(3)补充简单分式函数值域:例如,求函数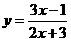 、
、 、(变量分离法)
、(变量分离法)
 的值域.
的值域.
(4)复合函数值域:例如,求函数 ,
, 的值域.
的值域.
3. 函数的定义域:理解求函数定义域的基本思想和方法,适度增加简单抽象函数定义域.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com