
题目列表(包括答案和解析)
5.求函数值域(最值)的方法:
(1)配方法(2)换元法――通过换元把一个较复杂的函数变为简单易求值域的函数,其函数特征是函数解析式含有根式或三角函数公式模型,运用换元法时,要特别要注意新元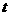 的范围)(3)函数有界性法――直接求函数的值域困难时,可以利用已学过函数的有界性,来确定所求函数的值域,最常用的就是三角函数的有界性(4)单调性法――利用一次函数,反比例函数,指数函数,对数函数等函数的单调性(5)数形结合法――函数解析式具有明显的某种几何意义,如两点的距离、直线斜率、等等(6)判别式法――对分式函数(分子或分母中有一个是二次)都可通用,但这类题型有时也可以用其它方法进行求解,不必拘泥在判别式法上,也可先通过部分分式后,再利用均值不等式:
的范围)(3)函数有界性法――直接求函数的值域困难时,可以利用已学过函数的有界性,来确定所求函数的值域,最常用的就是三角函数的有界性(4)单调性法――利用一次函数,反比例函数,指数函数,对数函数等函数的单调性(5)数形结合法――函数解析式具有明显的某种几何意义,如两点的距离、直线斜率、等等(6)判别式法――对分式函数(分子或分母中有一个是二次)都可通用,但这类题型有时也可以用其它方法进行求解,不必拘泥在判别式法上,也可先通过部分分式后,再利用均值不等式:
① 型,可直接用不等式性质,②
型,可直接用不等式性质,② 型,先化简,再用均值不等式
型,先化简,再用均值不等式
③ 型,通常用判别式法;
型,通常用判别式法;
④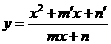 型,可用判别式法或均值不等式法
型,可用判别式法或均值不等式法
(7)不等式法――利用基本不等式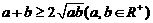 求函数的最值,其题型特征解析式是和式时要求积为定值,解析式是积时要求和为定值,不过有时须要用到拆项、添项和两边平方等技巧。
求函数的最值,其题型特征解析式是和式时要求积为定值,解析式是积时要求和为定值,不过有时须要用到拆项、添项和两边平方等技巧。
(8)导数法――一般适用于高次多项式函数,
提醒:(1)求函数的定义域、值域时,你按要求写成集合形式了吗?(2)函数的最值与值域之间有何关系?
4. 求函数定义域的常用方法(在研究函数问题时要树立定义域优先的原则)
复合函数的定义域:若已知 的定义域为
的定义域为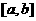 ,其复合函数
,其复合函数 的定义域由不等式
的定义域由不等式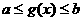 解出即可;若已知
解出即可;若已知 的定义域为
的定义域为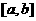 ,求
,求 的定义域,相当于当
的定义域,相当于当 时,求
时,求 的值域(即
的值域(即 的定义域)。
的定义域)。
3.同一函数的概念。构成函数的三要素是定义域,值域和对应法则。而值域可由定义域和对应法则唯一确定,因此当两个函数的定义域和对应法则相同时,它们一定为同一函数。
2.函数 : A
: A B是特殊的映射。特殊在定义域A和值域B都是非空数集!据此可知函数图像与
B是特殊的映射。特殊在定义域A和值域B都是非空数集!据此可知函数图像与 轴的垂线至多有一个公共点,但与
轴的垂线至多有一个公共点,但与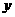 轴垂线的公共点可能没有,也可能有任意个。
轴垂线的公共点可能没有,也可能有任意个。
1.映射 : A
: A B
B
⑴A中元素必须都有象且唯一;
⑵B中元素不一定都有原象,但原象不一定唯一
27. 对数换底不等式及其推广
若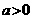 ,
, ,
,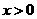 ,
, ,则函数
,则函数
(1)当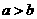 时,在
时,在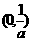 和
和 上
上 为增函数.
为增函数.
(2)当 时,在
时,在 和
和 上
上
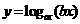 为减函数.
为减函数.
推论:设 ,
,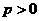 ,
, ,且
,且 ,则
,则
(1)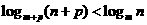 .
.
(2)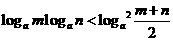 .
.
26.设函数 ,
,
记 .若
.若 的定义域为
的定义域为 ,则
,则 ,且
,且 ;若
;若 的值域为
的值域为 ,则
,则 ,且
,且 .对于
.对于 的情形,需要单独检验.
的情形,需要单独检验.
25.对数的四则运算法则
若a>0,a≠1,M>0,N>0,则
(1) ;
;
(2)  ;
;
(3) .
.
24.对数的换底公式
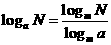 (
( ,且
,且 ,
, ,且
,且 ,
,  ).
).
推论  (
( ,且
,且 ,
, ,且
,且 ,
, ,
,  ).
).
23.指数式与对数式的互化式
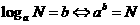
 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com