8．(天津文10) 设f(x)是定义在R上以6为周期的函数，f(x)在(0,3)内单调递减，且y=f(x)的图象关于直线x=3对称，则下面正确的结论是　　　　　　　　　　　 (　 　)

(A)；　　 (B)；

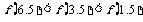(C)；　　 (D)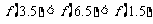

7.(山东卷)已知定义在R上的奇函数f(x)满足f(x+2)=－f(x),则,f(6)的值为

(A)－1　　　　　 (B) 0　　　　　　 (C)　 1　　　　　　　　 (D)2

6．(全国II)如果函数y=f(x)的图像与函数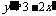的图像关于坐标原点对称，则y=f(x)的表达式为

(A)y=2x-3　　(B)y=2x+3　　　 (C)y=-2x+3　(D)y=-2x-3

5．(全国II)函数y＝f(x)的图像与函数g(x)＝log₂x(x＞0)的图像关于原点对称，则f(x)的表达式为

(A)f(x)＝(x＞0)　 (B)f(x)＝log₂(－x)(x＜0) 　

(C)f(x)＝－log₂x(x＞0)　 　(D)f(x)＝－log₂(－x)(x＜0)

4．(辽宁卷)设f(x)是R上的任意函数,则下列叙述正确的是

(A) f(x) f(-x)是奇函数 　(B) f(x) |f(-x)|是奇函数 　

(C) f(x)- f(-x)是偶函数 　(D) f(x)+ f(-x)是偶函数

3．(广东卷)下列函数中，在其定义域内既是奇函数又是减函数的是

A.　　 B. 　　

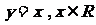C. 　　D.

2.(福建卷)已知f(x)是周期为2的奇函数，当0<x<1时，设则

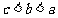(A)　　(B)　　(C)　　(D)

1.(北京卷)已知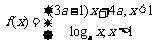是上的减函数，那么的取值范围是

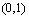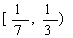(A)　 　 (B)　　 (C)　　 (D)

11．(全国II)设函数f(x)＝(x+1)ln(x+1)，若对所有的x≥0，都有f(x)≥ax成立，求实数a的取值范围．

解法一：令g(x)＝(x+1)ln(x+1)－ax，

对函数g(x)求导数：g′(x)＝ln(x+1)+1－a 令g′(x)＝0，解得x＝e^a－1－1，　　 ……5分

(i)当a≤1时，对所有x＞0，g′(x)＞0，所以g(x)在[0，+∞)上是增函数，

又g(0)＝0，所以对x≥0，都有g(x)≥g(0)，

即当a≤1时，对于所有x≥0，都有　f(x)≥ax．……9分

(ii)当a＞1时，对于0＜x＜e^a－1－1，g′(x)＜0，所以g(x)在(0，e^a－1－1)是减函数，

又g(0)＝0，所以对0＜x＜e^a－1－1，都有g(x)＜g(0)，即当a＞1时，对所有的x≥0，都有f(x)≥ax成立．

综上，a的取值范围是(－∞，1]．　　 ……12分

解法二：令g(x)＝(x+1)ln(x+1)－ax，于是不等式f(x)≥ax成立

即为g(x)≥g(0)成立．　……3分

对函数g(x)求导数：g′(x)＝ln(x+1)+1－a令g′(x)＝0，解得x＝e^a－1－1，　　 　……6分

当x＞ e^a－1－1时，g′(x)＞0，g(x)为增函数，

当－1＜x＜e^a－1－1，g′(x)＜0，g(x)为减函数，　　 ……9分

所以要对所有x≥0都有g(x)≥g(0)充要条件为e^a－1－1≤0．由此得a≤1，即a的取值范围是(－∞，1]．

10．(全国卷I)设为实数，函数在和都是增函数，求的取值范围。

解:f'(x)=3x²－2ax+(a²－1),其判别式△=4a²－12a²+12=12－8a².

(ⅰ)若△=0,即a=±,当x∈(－∞,),或x∈(,+∞)时,

f'(x)>0,f(x)在(－∞,+∞)为增函数.所以a=±.

(ⅱ)若△=12－8a²<0,恒有f'(x)>0,f(x)在(－∞,+∞)为增函数,

所以a²>,即a∈(－∞,－)∪(,+∞)

(ⅲ)若△12－8a²>0,即－<a<,令f'(x)=0,解得x₁=,x₂=.

当x∈(－∞,x₁),或x∈(x₂,+∞)时,f'(x)>0,f(x)为增函数;当x∈(x₁,x₂)时,f'(x)<0,f(x)为减函数.依题意x₁≥0且x₂≤1.由x₁≥0得a≥,解得1≤a<

由x₂≤1得≤3－a,解得－<a<,从而a∈[1,)

综上,a的取值范围为(－∞,－]∪[,+∞)∪[1,),即a∈(－∞,－]∪[1,∞).