
题目列表(包括答案和解析)
4.(06浙江卷)对a,b R,记max{a,b}=
R,记max{a,b}=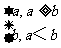 ,函数f(x)=max{|x+1|,|x-2|}(x
,函数f(x)=max{|x+1|,|x-2|}(x R)的最小值是____.
R)的最小值是____.
解:当x<-1时,|x+1|=-x-1,|x-2|=2-x,因为(-x-1)-(2-x)=-3<0,所以2-x>-x-1;当-1£x<0.5时,|x+1|=x+1,|x-2|=2-x,因为(x+1)-(2-x)=2x-1<0,x+1<2-x;当0.5£x<2时,x+1³2-x;当x³2时,|x+1|=x+1,|x-2|=x-2,显然x+1>x-2;
故 据此求得最小值为
据此求得最小值为 。选C
。选C
3.(07陕西卷)函数f(x)= (x∈R)的值域是( )
A.(0,1) B.(0,1] C.[0,1) D.[0,1]
2.(06湖南卷)函数 的定义域是_______ [4, +∞)
的定义域是_______ [4, +∞)
1.(06湖北卷)设 ,则
,则 的定义域为_______________
的定义域为_______________
解:f(x)的定义域是(-2,2),故应有-2<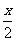 <2且-2<
<2且-2< <2解得-4<x<-1或1<x<4故选B
<2解得-4<x<-1或1<x<4故选B
12.设a为实数,设函数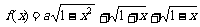 的最大值为g(a)。
的最大值为g(a)。
(Ⅰ)设t=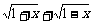 ,求t的取值范围,并把f(x)表示为t的函数m(t)
,求t的取值范围,并把f(x)表示为t的函数m(t)
(Ⅱ)求g(a)
解:本小题主要考查函数、方程等基本知识,考查分类讨论的数学思想方法和综合运用数学知识分析问题、解决问题的能力。
(Ⅰ)令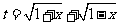
要使有t意义,必须1+x≥0且1-x≥0,即-1≤x≤1,
∴ t≥0
①
t≥0
①
t的取值范围是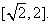 由①得
由①得
∴m(t)=a( )+t=
)+t=
(Ⅱ)由题意知g(a)即为函数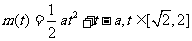 的最大值。
的最大值。
注意到直线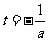 是抛物线
是抛物线 的对称轴,分以下几种情况讨论。
的对称轴,分以下几种情况讨论。
(1)当a>0时,函数y=m(t), 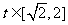 的图象是开口向上的抛物线的一段,
的图象是开口向上的抛物线的一段,
由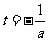 <0知m(t)在
<0知m(t)在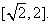 上单调递增,∴g(a)=m(2)=a+2
上单调递增,∴g(a)=m(2)=a+2
(2)当a=0时,m(t)=t, 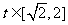 ,∴g(a)=2.
,∴g(a)=2.
(3)当a<0时,函数y=m(t), 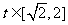 的图象是开口向下的抛物线的一段,
的图象是开口向下的抛物线的一段,
若 ,即
,即 则
则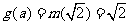
若 ,即
,即 则
则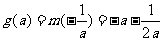
若 ,即
,即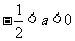 则
则
综上有
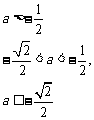
11.定义在R上的函数y=f(x),f(0)≠0,当x>0时,f(x)>1,且对任意的a、b∈R,有f(a+b)=f(a)f(b),(1)求证:f(0)=1;(2)求证:对任意的x∈R,恒有f(x)>0;
(3)证明:f(x)是R上的增函数;
点拨与提示:根据f(a+b)=f(a)·f(b)是恒等式的特点,对a、b适当赋值.利用单调性的性质去掉符号“f”得到关于x的代数不等式,是处理抽象函数不等式的典型方法.
9.方程f(x)=x的根称为f(x)的不动点,若函数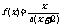 有唯一不动点,且
有唯一不动点,且 ,
, ,则
,则 。
。
8.已知f(x)是R上的偶函数,对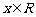 都有f(x+6)=f(x)+f(3)成立,若f(1)=2,则f(2005)=( )
都有f(x+6)=f(x)+f(3)成立,若f(1)=2,则f(2005)=( )
A、2005 B、2 C、1 D、0
7.(甘肃贵州青海宁夏新疆)理科数学第12题]
设函数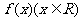 为奇函数,
为奇函数, 则
则 ( )
( )
A.0 B.1 C. D.5
D.5
6.(山东卷理4)下列函数既是奇函数,又在区间 上单调递减的是( D )
上单调递减的是( D )
(A) (B)
(B)
(C) (D)
(D)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com