14、抛物线y=ax²与直线y=kx+b(k≠0)交于A、B两点，且此两点的横坐标分别为x₁,x₂,直线与x轴交点的横坐标是x₃,则恒有(　　 )

A.x₃=x₁+x₂ 　B.x₁x₂=x₁x₃+x₂x₃ C.x₁+x₂+x₃=0 D.x₁x₂+x₂x₃+x₃x₁=0

解析：解方程组,得ax²－kx－b=0,可知x₁+x₂=,x₁x₂=－,x₃=－,

代入验证即可.答案：B

13、中心在原点，焦点在坐标为(0，±5)的椭圆被直线3x－y－2=0截得的弦的中点的横坐标为，则椭圆方程为(　　 )

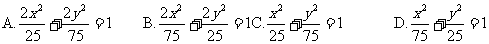
解析：由题意，可设椭圆方程为： =1,且a²=50+b², 即方程为=1.

将直线3x－y－2=0代入，整理成关于x的二次方程.

由x₁+x₂=1可求得b²=25,a²=75.答案：C

12、△ABC中，A为动点，B、C为定点，B(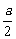－,0),C(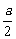,0)，且满足条件sinC－sinB=sinA,则动点A的轨迹方程为_________.

解析：由sinC－sinB=sinA,得c－b=a,

∴应为双曲线一支，且实轴长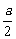为,故方程为.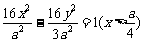

答案：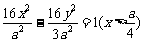

11、设A₁、A₂是椭圆=1的长轴两个端点，P₁、P₂是垂直于A₁A₂的弦的端点，则直线A₁P₁与A₂P₂交点的轨迹方程为　　　　　　 。

解析：设交点P(x,y),A₁(－3,0),A₂(3,0),P₁(x₀,y₀),P₂(x₀,－y₀)

∵A₁、P₁、P共线，∴∵A₂、P₂、P共线，∴

解得x₀=

10、已知椭圆的焦点是F₁、F₂，P是椭圆上的一个动点，如果延长F₁P到Q，使得|PQ|=|PF₂|，那么动点Q的轨迹是　　　　　 。

解析：∵|PF₁|+|PF₂|=2a,|PQ|=|PF₂|,∴|PF₁|+|PF₂|=|PF₁|+|PQ|=2a,

即|F₁Q|=2a,∴动点Q到定点F₁的距离等于定长2a,故动点Q的轨迹是圆.

9、设不等式2x－1＞m(x²－1)对一切满足|m|≤2的值均成立，则x的范围为_________.

原不等式变为(x²－1)m+(1－2x)＜0,构造线段f(m)=(x²－1)m+1－2x,－2≤m≤2,

则f(－2)＜0,且f(2)＜0.答案：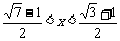

8、函数f(θ)=的最大值为_________，最小值为_________.

解析：f(θ)=表示两点(cosθ,sinθ)与(2,1)连线的斜率.答案：　 0

7、自点A(－3，3)发出的光线l射到x轴上，被x轴反射，其反射光线所在直线与

圆x²+y²－4x－4y+7=0相切，则光线l所在直线方程为_________.

解析：光线l所在的直线与圆x²+y²－4x－4y+7=0关于x轴对称的圆相切.

答案：3x+4y－3=0或4x+3y+3=0

6、直线2x－y－4=0上有一点P，它与两定点A(4，－1)，B(3，4)的距离之差最大，

则P点坐标是_________.

解析：找A关于l的对称点A′，A′B与直线l的交点即为所求的P点.答案：P(5，6)

5、已知函数f(x)= (b＜0)的值域是［1，3］，则b=　　　　 c=　　　　 。

解：设y=，则(y－2)x²－bx+y－c=0　　 　 ①

∵x∈R，∴①的判别式Δ≥0，即 b²－4(y－2)(y－c)≥0，即4y²－4(2+c)y+8c+b²≤0　 ②

由条件知，不等式②的解集是［1，3］∴1，3是方程4y²－4(2+c)y+8c+b²=0的两根

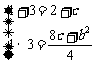∴c=2，b=－2，b=2(舍)