考试要求：1、掌握分类计数原理与分步计数原理，并能用它们分析和解决一些简单的应用问题。2、理解排列的意义，掌握排列数计算公式，并能用它解决一些简单的应用问题。

3、理解组合的意义，掌握组合数计算公式和组合数的性质，并能用它们解决一些简单的应用问题。4、掌握二项式定理和二项展开式的性质，并能用它们计算和证明一些简单的问题。

22．上海电信宽频私人用户月收费标准如下表

假定每月初可以和电信部门约定上网方案

1)某用户每月上网时间为70小时，应选择哪种方案

2)写出方案乙中每月总费用y(元)关于时间t(小时)的函数关系式

3)费先生一年内每月上网时间t(n)(小时)与月份n的函数为，问费先生全年的上网费用最少为多少元

21．已知

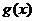(1), 求的最小值

(2)P、Q关于点(1，2)对称，若点P在曲线C上移动时，点Q的轨迹是函数的图象，求曲线C的轨迹方程。

(3)在中学数学中，从特殊到一般，从具体到抽象是常见的一种思维形式。如从可抽象出的性质，试分别写出一个具体的函数，抽象出下列相应的性质

由　　　　 可抽象出

由　　　　 可抽象出

20．曲线C上的动点P到定点Q(1，0)与它到直线x+1=0的距离相等。求：

(1)曲线C的方程；

　 (2)过点Q的直线与曲线C交于A、B两点，求证：为定值。

　 (温馨提示：　 ，则)

19．对于数列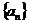，有，且,

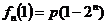
　 求:　 (1)p的值　　　　　　　　　

(2)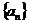的通项公式

18．曾记否？复数，。

已知 ,，求的取值范围。

17．长方体ABCD-A₁B₁C₁D₁中，M，N分别是BB₁和BC的中点，AB=4，AD=2，B₁D与平面ABCD所成角的大小为60^。，求异面直线B₁D与MN所成角的大小。

16．等差数列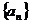的前n项和为S_n，已知,则(　　 )

(A)n=5时，S_n有最大值　　　　　 (B)n=6时，S_n有最大值

(C)n=5时，S_n有最小值　　　　　　 (D)n=6时，S_n有最小值

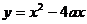15． 命题A：若x>0,则<1, 命题B：函数在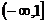上为减函数。

　 若A与B中至少有一个是真命题，则实数a的取值范围是(　　 )

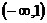　 (A)　　　　 (B)　　　 (C)　　　 (D)

14． y=f(x),y=g(x)的图象如下,f(1)=g(2)=0,则不等式的解集是(　　 )

(A) (B)

(C) (D)