
题目列表(包括答案和解析)
9.已知二次函数 的导数为
的导数为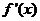 ,
, ,对于任意实数
,对于任意实数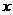 都有
都有 ,则
,则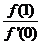 的最小值为
的最小值为
A.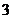 B.
B.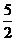 C.
C.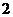 D.
D.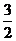
8.设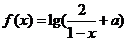 是奇函数,则使
是奇函数,则使 的
的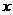 的取值范围是
的取值范围是
A.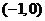 B.
B.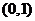 C.
C.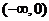 D.
D.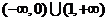
7.若对于任意实数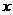 ,有
,有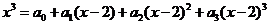 ,则
,则 的值为
的值为
A.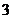 B.
B. C.
C. D.
D.
6.设函数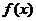 定义在实数集上,它的图像关于直线
定义在实数集上,它的图像关于直线 对称,且当
对称,且当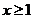 时,
时,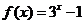 ,则有
,则有
A.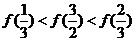 B.
B.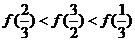
C.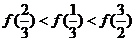 D.
D.
5.函数 的单调递增区间是
的单调递增区间是
A. B.
B. C.
C.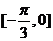 D.
D.
4.已知两条直线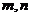 ,两个平面
,两个平面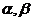 ,给出下面四个命题:
,给出下面四个命题:
①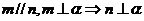 ②
②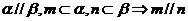
③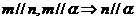 ④
④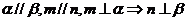
其中正确命题的序号是
A.①③ B.②④ C.①④ D.②③
3.在平面直角坐标系 中,双曲线中心在原点,焦点在
中,双曲线中心在原点,焦点在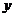 轴上,一条渐近线方程为
轴上,一条渐近线方程为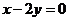 ,则它的离心率为
,则它的离心率为
A. B.
B. C.
C.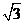 D.
D.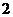
2.已知全集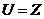 ,
,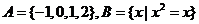 ,则
,则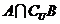 为
为
A.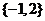 B.
B.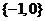 C.
C. D.
D.
1.下列函数中,周期为 的是
的是
A. B.
B.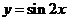 C.
C. D.
D.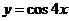
例1.(07天津卷)已知函数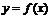 的图象与函数
的图象与函数 (
( 且
且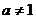 )的图象关于直线
)的图象关于直线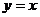 对称,记
对称,记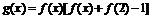 .若
.若 在区间
在区间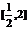 上是增函数,则实数
上是增函数,则实数 的取值范围是( )
的取值范围是( )
A.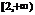 B.
B.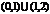 C.
C.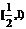 D.
D.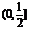
例2.(06天津卷)如果函数 在区间
在区间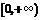 上是增函数,那么实数
上是增函数,那么实数 的取值范围是() A.
的取值范围是() A.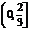 B.
B.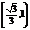 C.
C. D.
D.
例3.(06上海卷)方程 的解是_____.5
的解是_____.5
例4.(07重庆卷)设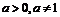 ,函数
,函数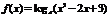 有最小值,则不等式
有最小值,则不等式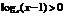 的解集为
。x>2
的解集为
。x>2
例5. (06重庆卷)已知定义域为R的函数 是奇函数。(Ⅰ)求
是奇函数。(Ⅰ)求 的值; (Ⅱ)若对任意的
的值; (Ⅱ)若对任意的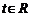 ,不等式
,不等式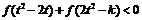 恒成立,求k的取值范围;
恒成立,求k的取值范围;
解析:(Ⅰ)因为f(x)是奇函数,所以f(0)=0,即
又由f(1)= -f(-1)知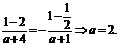
(Ⅱ)解法一:由(Ⅰ)知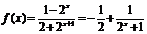 ,
,
易知f(x)在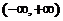 上为减函数。又因f(x)是奇函数,从而不等式:
上为减函数。又因f(x)是奇函数,从而不等式:
 等价于
等价于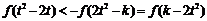 ,
,
因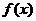 为减函数,由上式推得:
为减函数,由上式推得: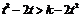 .即对一切
.即对一切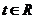 有:
有: ,
,
从而判别式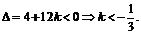
解法二:由(Ⅰ)知 .又由题设条件得:
.又由题设条件得: 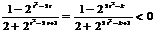 ,
,
即 :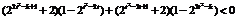 ,
,
整理得 
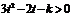 上式对一切
上式对一切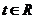 均成立,
均成立,
从而判别式
例6.证明不等式: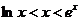
例7.定义在R上的单调函数f(x)满足f(3)=log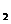 3且对任意x,y∈R都有f(x+y)=f(x)+f(y).(1)求证f(x)为奇函数;
3且对任意x,y∈R都有f(x+y)=f(x)+f(y).(1)求证f(x)为奇函数;
(2)若f(k·3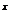 )+f(3
)+f(3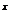 -9
-9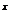 -2)<0对任意x∈R恒成立,求实数k的取值范围.
-2)<0对任意x∈R恒成立,求实数k的取值范围.
解: (1)证明:f(x+y)=f(x)+f(y)(x,y∈R), ①
令x=y=0,代入①式,得f(0+0)=f(0)+f(0),即 f(0)=0.
令y=-x,代入①式,得 f(x-x)=f(x)+f(-x),又f(0)=0,
则有0=f(x)+f(-x).即f(-x)=-f(x)对任意x∈R成立,
所以f(x)是奇函数.
(2)解:f(3)=log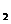 3>0,即f(3)>f(0),又f(x)在R上是单调函数,所以f(x)在R上是增函数,
3>0,即f(3)>f(0),又f(x)在R上是单调函数,所以f(x)在R上是增函数,
又由(1)f(x)是奇函数.f(k·3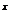 )<-f(3
)<-f(3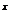 -9
-9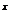 -2)=f(-3
-2)=f(-3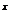 +9
+9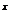 +2),
+2),
∴ k·3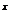 <-3
<-3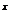 +9
+9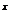 +2,3
+2,3 -(1+k)·3
-(1+k)·3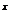 +2>0对任意x∈R成立.
+2>0对任意x∈R成立.
令t=3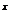 >0,问题等价于t
>0,问题等价于t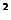 -(1+k)t+2>0
-(1+k)t+2>0
对任意t>0恒成立.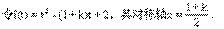
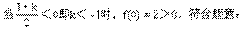
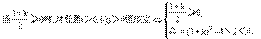
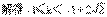
 R恒成立.
R恒成立.
例8.在xOy平面上有一点列P1(a1,b1),P2(a2,b2),…,Pn(an,bn)…,对每个自然数n点Pn位于函数y=2000(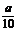 )x(0<a<1)的图象上,且点Pn,点(n,0)与点(n+1,0)构成一个以Pn为顶点的等腰三角形
)x(0<a<1)的图象上,且点Pn,点(n,0)与点(n+1,0)构成一个以Pn为顶点的等腰三角形 (1)求点Pn的纵坐标bn的表达式;(2)若对于每个自然数n,以bn,bn+1,bn+2为边长能构成一个三角形,求a的取值范围;(3)设Cn=lg(bn)(n∈N*),若a取(2)中确定的范围内的最小整数,问数列{Cn}前多少项的和最大?试说明理由
(1)求点Pn的纵坐标bn的表达式;(2)若对于每个自然数n,以bn,bn+1,bn+2为边长能构成一个三角形,求a的取值范围;(3)设Cn=lg(bn)(n∈N*),若a取(2)中确定的范围内的最小整数,问数列{Cn}前多少项的和最大?试说明理由
解 (1)由题意知
(1)由题意知 an=n+
an=n+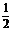 ,∴bn=2000(
,∴bn=2000(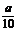 )
)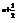

(2)∵函数y=2000(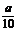 )x(0<a<10)递减,∴对每个自然数n,有bn>bn+1>bn+2
)x(0<a<10)递减,∴对每个自然数n,有bn>bn+1>bn+2
则以bn,bn+1,bn+2为边长能构成一个三角形的充要条件是bn+2+bn+1>bn,
即(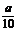 )2+(
)2+(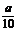 )-1>0,
)-1>0,
解得a<-5(1+ )或a>5(
)或a>5(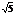 -1)
-1) ∴5(
∴5(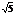 -1)<a<10
-1)<a<10
(3)∵5(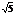 -1)<a<10,∴a=7∴bn=2000(
-1)<a<10,∴a=7∴bn=2000( )
)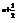
 数列{bn}是一个递减的正数数列,
数列{bn}是一个递减的正数数列,
对每个自然数n≥2,Bn=bnBn-1 于是当bn≥1时,Bn<Bn-1,当bn<1时,Bn≤Bn-1,
于是当bn≥1时,Bn<Bn-1,当bn<1时,Bn≤Bn-1,
因此数列{Bn}的最大项的项数n满足不等式bn≥1且bn+1<1,
由bn=2000( )
)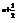 ≥1得
≥1得 n≤20
n≤20 8
8 ∴n=20
∴n=20
例9.已知 ,设P:函数
,设P:函数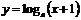 在x∈(0,+∞)上单调递减;Q:曲线
在x∈(0,+∞)上单调递减;Q:曲线 与x轴交于不同两点,如果P和Q有且仅有一个正确,求
与x轴交于不同两点,如果P和Q有且仅有一个正确,求 的取值范围。
的取值范围。
例10.(06福建卷)已知函数f(x)=-x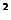 +8x,g(x)=6lnx+m
+8x,g(x)=6lnx+m
(Ⅰ)求f(x)在区间[t,t+1]上的最大值h(t);
(Ⅱ)是否存在实数m,使得y=f(x)的图象与y=g(x)的图象有且只有三个不同的交点?若存在,求出m的取值范围;,若不存在,说明理由。
本小题主要考查函数的单调性、极值等基本知识,考查运用导数研究函数的性质的方法,考查函数与方程、数形结合等数学思想方法和分析问题、解决问题的能力。满分12分。
本小题主要考查函数的单调性、极值、最值等基本知识,考查运用导数研究函数性质
的方法,考查运算能力,考查函数与方程、数形结合、分类与整合等数学思想方法和分析问题、解决问题的能力。
解:(I)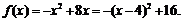
当t+1<4即t<3时,f(x)在[t,t+1]上单调递增,
当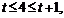 即
即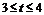 时,
时,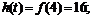
当t>4时,f(x)在[t,t+1]上单调递减,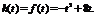 综上,
综上,
(II)函数y=f(x)的图象与y=g(x)的图象有且只有三个不同的交点,即函数
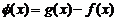 的图象与
的图象与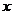 轴的正半轴有且只有三个不同的交点。
轴的正半轴有且只有三个不同的交点。

当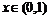 时,
时,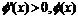 是增函数;
是增函数;
当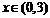 时,
时,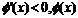 是减函数;
是减函数;
当 时,
时,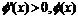 是增函数;
是增函数;
当x=1或x=3时,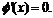

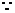 当x充分接近0时,
当x充分接近0时,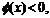 当x充分大时,
当x充分大时,
 要使
要使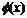 的图象与
的图象与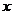 轴正半轴有三个不同的交点,必须且只须
轴正半轴有三个不同的交点,必须且只须
即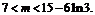 所以存在实数m,使得函数y=f(x)与y=g(x)的图象有且只有三个不同的交点,m的取值范围为(7,15-6ln3)
所以存在实数m,使得函数y=f(x)与y=g(x)的图象有且只有三个不同的交点,m的取值范围为(7,15-6ln3)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com