
题目列表(包括答案和解析)
2. 在△ABC中,“sin2A>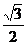 ”
” 是“A>15
是“A>15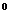 ”的( )
”的( )
A.充分不必要条件 B。必要不充分条件
C.充要条件 D。既不充分也不必要条件
1. 已知集合P={ 0, m},Q={x│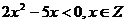 },若P∩Q≠
},若P∩Q≠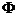 ,则m等于( )
,则m等于( )
A.1
B.2
C.1或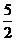 D. 1或2
D. 1或2
21、(1)解:设P(a,0),Q(0,b)则: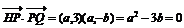 ∴
∴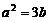 …………1分 设M(x,y)∵
…………1分 设M(x,y)∵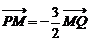 ∴
∴
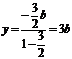 …4分 ∴点M的轨迹曲线C的方程是
…4分 ∴点M的轨迹曲线C的方程是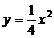 (x≠0) .6分
(x≠0) .6分
(2)解法一:设A(a,b),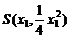 ,
,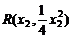 (x1≠x2)
(x1≠x2)
则:直线SR的方程为: ,即4y = (x1+x2)x-x1x2 ∵A点在SR上,∴4b=(x1+x2)a-x1x2 ①
…………8分
,即4y = (x1+x2)x-x1x2 ∵A点在SR上,∴4b=(x1+x2)a-x1x2 ①
…………8分
对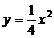 求导得:y′=
求导得:y′=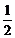 x∴抛物线上S、R处的切线方程为:
x∴抛物线上S、R处的切线方程为:
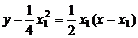 即4
即4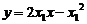 ②
②
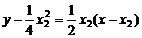 即4
即4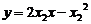 ③
…………11分
③
…………11分
联立②③,并解之得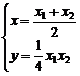 ,代入①得:ax-2y-2b=0
,代入①得:ax-2y-2b=0
故B点恒在直线ax-2y-2b=0上. …………14分
解法二:设A(a,b)
当过点A的直线斜率不存在时l与抛物线有且仅有一个公共点,与题意不符,可设直线SR的方程为y-b=k(x-a)与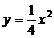 联立消去y得:x2-4kx+4ak-4b=0 …8分 设
联立消去y得:x2-4kx+4ak-4b=0 …8分 设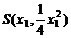 ,
,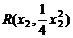 (x1≠x2)
(x1≠x2)
则由韦达定理: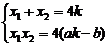 …………9分
…………9分
又过S、R点的切线方程分别为: ,
,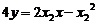 …11分
…11分
故有 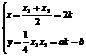 (k为参数)消去k,得:ax-2y-2b=0
(k为参数)消去k,得:ax-2y-2b=0
故B点恒在直线ax-2y-2b=0上. …………14分
19、解:(1)依题意知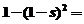
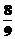 , ∴s=
, ∴s=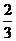 .
………3分
.
………3分
(2)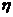 的取值可以是0,1,2.…………………………5分
的取值可以是0,1,2.…………………………5分
甲、乙两人命中10环的次数均为0次的概率是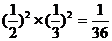 ,
,
甲、乙两人命中10环的次数均为1次的概率是 ,
,
甲、乙两人命中10环的次数均为2次的概率是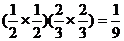 ,
,
∴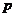 (
(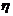 =0)=
=0)=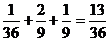 .
…………8分
.
…………8分
甲命中10环的次数为2次且乙命中10环的次数为0次的概率是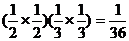 ,
,
甲命中10环的次数为0次且乙命中10环的次数为2次的概率是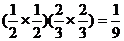 .∴
.∴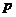 (
(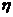 =2)=
=2)=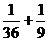 =
=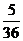 , ……11分
, ……11分
∴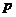 (
(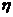 =1)=1
=1)=1 (
(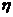 =0)
=0) (
(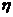 =2)=
=2)=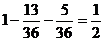 . ……14分
. ……14分
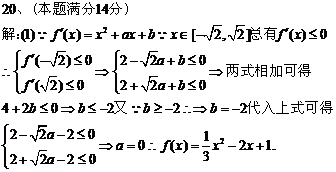
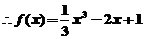

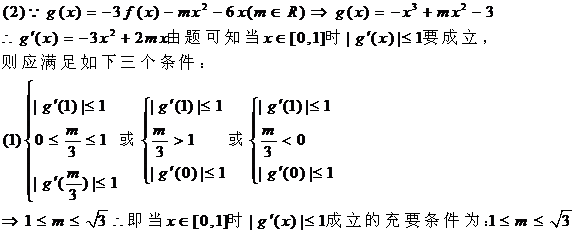
18、(1)解法一:联结AC交DB于点O. ∵ABCD是正方形,∴AC⊥DB.
又PD⊥平面ABCD,AC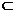 平面ABCD, ∴AC⊥PD, ∴AC⊥平面PBD.
平面ABCD, ∴AC⊥PD, ∴AC⊥平面PBD.
作OF⊥PB于点F,联结AF,则AF⊥PB.
∴∠OFA就是二面角A-PB-D的平面角. …………2分
∵PD⊥平面ABCD,AB⊥AD,∴PA⊥AB.
令PD=AD=2,则在RT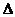 ABC中,PA=
ABC中,PA= ,AB=2.
,AB=2.
∴PB=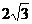 ,∴
,∴ .
.
∴在RT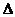 AOF中,sin
AOF中,sin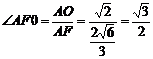 ,∴
,∴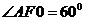 .
.
∴二面角A-PB-D的大小为 . …………7分
. …………7分
解法二:建立如图所示的直角坐标系.
联结AC,交BD于点O,取PA中点G,联结DG.
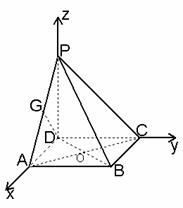 ∵ABCD是正方形,∴AC⊥DB.
∵ABCD是正方形,∴AC⊥DB.
又PD⊥平面ABCD,AC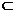 平面ABCD,
平面ABCD,
∴AC⊥PD, ∴AC⊥平面PBD.
∵PD⊥平面ABCD,AB⊥AD,∴PA⊥AB.
∴AB⊥平面PAD.
∵PD=AD,G为PA中点, ∴GD⊥平面PAB.
故向量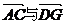 分别是平面PBD与平面PAB的法向量.
分别是平面PBD与平面PAB的法向量.
令PD=AD=2,则A(2,0,0),C(0,2,0),∴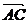 =(-2,2,0).
=(-2,2,0).
∵P(0,0,2),A(2,0,0), ∴G(1,0,1),∴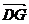 =(1,0,1). …………4分
=(1,0,1). …………4分
∴向量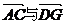 的夹角余弦为
的夹角余弦为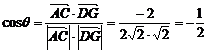 ,
,
∴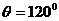 ,∴二面角A-PB-D的大小为
,∴二面角A-PB-D的大小为 . ………7分
. ………7分
 (2)解法一: 当点E是线段PB中点时,
(2)解法一: 当点E是线段PB中点时,
有PC⊥平面ADE. …7分
证明如下:
取PC中点H,联结EH,DH,则有EH∥BC,
又BC∥AD,故有EH∥AD.
∴平面ADE即平面ADHE. …………9分
∵PD=DC,H为PC中点, ∴PC⊥DH.
又∵PD⊥平面ABCD,AD⊥CD,∴AD⊥PC.
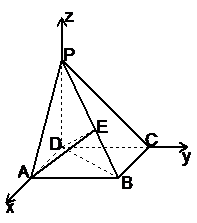 ∴PC⊥平面ADHE,即PC⊥平面ADE.
…………14分
∴PC⊥平面ADHE,即PC⊥平面ADE.
…………14分
解法二:建立如图所示的直角坐标系.
∵PD⊥平面ABCD,AD⊥CD,∴AD⊥PC.
设E是线段PB上的一点,令 .
.
令PD=AD=2,则P(0,0,2),A(2,0,0),B(2,2,0),
C(0,2,0),
∴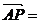 (-2,0,2),
(-2,0,2),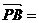 (2,2,-2),
(2,2,-2), (0,2,-2).
(0,2,-2).
∴ .
.
∴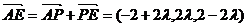 .
.
令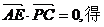 2
2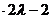 (
(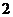 -
-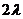 )=0,得
)=0,得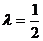 .
.
∴当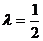 ,即点E是线段PB中点时,有AE⊥PC.
,即点E是线段PB中点时,有AE⊥PC.
又∵PD⊥平面ABCD,AD⊥CD,∴AD⊥PC.
∴当点E是线段PB中点时,有PC⊥平面ADE. …………14分
17、解:(1)由已知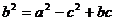 ,得
,得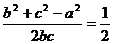
∴ ,∴
,∴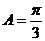 . …………6分
. …………6分
(2)
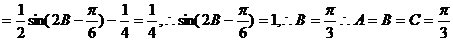
∴△ABC为等边三角形。 …………12分
16、解:(1)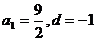 …………4分
…………4分
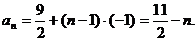 ………………6分
………………6分
(2)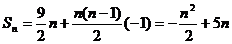 ………………9分
………………9分
当n=5时Sn取大值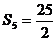 ………………12分
………………12分
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
B |
B |
A |
D |
C |
A |
C |
D |
D |
A |
21、(本小题满分14分)已知点H(0,―3),点P在x轴上,点Q在y轴正半轴上,点M在直线PQ上,且满足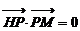 ,
,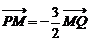 .
.
(1)当点P在x轴上移动时,求动点M的轨迹曲线C的方程; (2)过定点A(a,b)的直线与曲线C相交于两点S、R,求证:曲线C在S、R 两点处的切线的交点B恒在一条直线上.
(文科)1答案
20、 (本小题满分14分)函数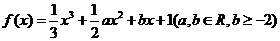 ,
,
当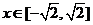 ,总有
,总有 .
.
(1)求函数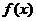 的解析式;
的解析式;
(2)设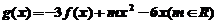 ,求证:当
,求证:当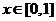 时,
时,  成立的充要条件是:
成立的充要条件是: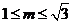
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com