
题目列表(包括答案和解析)
20.(本题14分。第(1)题7分,第(2)题7分)
已知椭圆C1: =1(a>b>0)的一条准线方程为
=1(a>b>0)的一条准线方程为 。其左、右顶点分别是A、B;双曲线C2:
。其左、右顶点分别是A、B;双曲线C2: =1的一条渐近线方程为3x-5y=0。
=1的一条渐近线方程为3x-5y=0。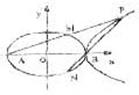
(1)求椭圆C1的方程及双曲线C2的离心率。



 (2)在第一象限内,取双曲线C2上的一点P,连结AP交椭圆C1于点M,连结PB并延长交椭圆C1于点N,若AM=MP,求证:MN·AB=0
(2)在第一象限内,取双曲线C2上的一点P,连结AP交椭圆C1于点M,连结PB并延长交椭圆C1于点N,若AM=MP,求证:MN·AB=0
19.(本题14分)某学校为了解决教职工的住房问题,计划征用一块土地盖一幢总面积为A(m2)的宿舍楼。已知土地的征用费为2388元/m2,且每层的建筑面积相同,土地的征用面积为第一层的2.5倍。经工程技术人员核算,第一、二层的建筑费用相同,都为445元/m2,以后每增高一层,其建筑费用就增加30元/m2。试设计这幢宿舍楼的楼高层数,使总费用最少,并求出其最少费用。(总费用为建筑费用与征地费用之和。)
18、(本题共14分)
设数列{an}和{bn}满足a1=b1=6,a2=b2=4,a3=b3=3,且数列{an+1-an}(n∈N*)是等差数列,数列{bn-2} (n∈N*)是等比数列。
(1)设Cn=an+1-an,求数列{Cn}的通项公式
(2)求数列{an}和{bn}的通项公式。
(3) 是否存在k∈N*,使得ak-bk∈(0, )?若存在,求出k;若不存在,请说明理由。
)?若存在,求出k;若不存在,请说明理由。
17.(本题12分。第①题5分,第②题7分)
如图,正四棱柱ABCD-A1B1C1D1,AA1= AB,点E、M分别为A1B,C1C的中点,过A1、B、M三点的平面A1BMN交C1D1于点N。
AB,点E、M分别为A1B,C1C的中点,过A1、B、M三点的平面A1BMN交C1D1于点N。
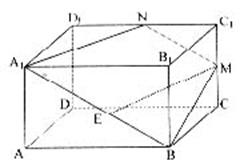 ①求证:EM∥A1B1C1D1
①求证:EM∥A1B1C1D1
②求二面角B-A1N-B1正切值。
16.(本题共12分,第①小题4分,第②小题4分,第③小题4分)
已知f(x)=2sin(x+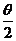 )cos (x+
)cos (x+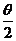 )+2
)+2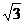 cos2(x+
cos2(x+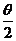 )-
)-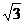
①求f(x)的最小正周期
②若0≤ ≤
≤ 求使f(x)为偶函数的
求使f(x)为偶函数的 的值。
的值。
③在②条件下,求满足f(x)=1,
x∈[- ]的x的集合。
]的x的集合。
15.一天内的不同的时刻,经理把文件交由秘书打字。每次都将文件堆放在秘书的文件堆的上面,秘书有时间就将文件最上面的那份文件取来打字。若有5份文件,且经理是按1,2,3,4,5的顺序交来的,在下列的顺序①12345,②32415,③24351,④54321,⑤45231中,秘书打字的可能顺序是________(只要填上序号).
14.已知 、
、 是实数,给出下列四个论断:(1)
是实数,给出下列四个论断:(1) ,(2)
,(2) ,(3)
,(3)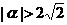 ,
, ,(4)
,(4) .以其中的两个论断为条件,其余两个论断作为结论,写出你认为正确的一个命题:________.
.以其中的两个论断为条件,其余两个论断作为结论,写出你认为正确的一个命题:________.
13.函数 的单调递减区间是______________.
的单调递减区间是______________.
12.已知一个球的半径为1,若使其表面积增加到原来的2倍,则表面积增加后球的体积是______________.
11.设双曲线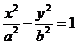 的右准线与两条渐近线交于A、B两点,右焦点为F,且FA⊥FB,则双曲线的离心率为( ).
的右准线与两条渐近线交于A、B两点,右焦点为F,且FA⊥FB,则双曲线的离心率为( ).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com