
题目列表(包括答案和解析)
6.(Ⅰ)P(两人都投进两球)=
 =
=
(Ⅱ)P(两人至少投进三个球)=
第二课时
例题
例1 甲、乙二人参加普法知识竞答,共有10个不同的题目,其中选择题6个,判断题4个,甲、乙二人依次各抽一题.
(Ⅰ)甲抽到选择题、乙抽到判断题的概率是多少?
(Ⅱ)甲、乙二人中至少有一人抽到选择题的概率是多少?(2000年新课程卷)
例2 如图,用A、B、C三类不同的元件连接成两个系统N1、N2.当元件A、B、C都正常工作时,系统N1正常工作;当元件A正常工作且元件B、C至少有一个正常工作时,系统N2正常工作.已知元件A、B、C正常工作的概率依次为0.80,0.90,0.90.分别求系统N1、N2正常工作的概率P1、P2. (2001年新课程卷)

例3 某单位6个员工借助互联网开展工作,每个员工上网的概率都是0.5(相互独立).
(Ⅰ)求至少3人同时上网的概率;
(Ⅱ)至少几人同时上网的概率小于0.3?(2002年新课程卷)
例4 有三种产品,合格率分别是0.90,0.95和0.95,各抽取一件进行检验.
(Ⅰ)求恰有一件不合格的概率;
(Ⅱ)求至少有两件不合格的概率.(精确到0.001) (2003年新课程卷)
备用 从分别写有0,1,2,3,4,5,6的七张卡片中,任取4张,组成没有重复数字的四位数,计算:
(1)这个四位数是偶数的概率;
(2)这个四位数能被9整除的概率;
(3)这个四位数比4510大的概率。
解: (1)组成的所有四位数共有 个。四位偶数有:个位是0时有
个。四位偶数有:个位是0时有 ,个位不是0时有
,个位不是0时有 ,共有120+300=420个.
,共有120+300=420个.
 组成的四位数为偶数的概率为
组成的四位数为偶数的概率为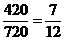
(2)能被9整除的数,应该各位上的数字和能被9整除.数字组合为:1,2,6,0 1,3,5,0 2,4,5,0
3,4,5,6 2,3,4,0 此时共有 .
.
 能被9整除的四位数的概率为
能被9整除的四位数的概率为
(3)比4510大的数分别有:千位是4,百位是5时,有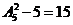 ;千位是4,百位是6时,有
;千位是4,百位是6时,有 ;千位大于4时,有
;千位大于4时,有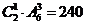 ;故共有240+20+18=278.
;故共有240+20+18=278.
 四位数且比4510大的概率为
四位数且比4510大的概率为
作业
5.(Ⅰ)P(A+B)= P(A)+P(B)= =
= ; (Ⅱ) P=
; (Ⅱ) P= -
- =
=
1. B 2. D 3. 0.05 4. 
6. 已知甲、乙两人投篮的命中率分别为0.4和0.6.现让每人各投两次,试分别求下列事件的概率:(Ⅰ)两人都投进两球;(Ⅱ)两人至少投进三个球.
作业答案
5. 袋中有大小相同的5个白球和3个黑球,从中任意摸出4个,求下列事件发生的概率.
(Ⅰ)摸出2个或3个白球 ; (Ⅱ)至少摸出一个黑球.
4. 若在二项式(x+1)10的展开式中任取一项,则该项的系数为奇数的概率是 .
(结果用分数表示)
3. 从含有500个个体的总体中一次性地抽取25个个体,假定其中每个个体被抽到的概率
相等,那么总体中的每个个体被抽取的概率等于_______。
2. 连续掷两次骰子,以先后得到的点数m、n为点P(m,n)的坐标,那么点P在圆x2+y2=17外部的概率应为( )
(A) (B)
(B)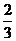 (C)
(C)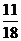 (D)
(D)
1. 甲、乙两人独立地解同一问题,甲解决这个问题的概率是p1,乙解决这个问题的概率
是p2,那么恰好有1人解决这个问题的概率是 ( )
(A) (B)
(B) (C)
(C)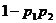 (D)
(D)
2. 已知两名射击运动员的射击水平,让他们各向目标靶射击10次,其中甲击中目标7次,乙击中目标6次,若在让甲、乙两人各自向目标靶射击3次中,求:(1)甲运动员恰好击中目标2次的概率是多少?(2)两名运动员都恰好击中目标2次的概率是多少?(结果保留两位有效数字)
解. 甲运动员向目标靶射击1次,击中目标的概率为7/10=0.7
乙运动员向目标靶射击1次,击中目标的概率为6/10=0.6
(1)甲运动员向目标靶射击3次,恰好都击中目标2次的概率是

(2)乙运动员各向目标靶射击3次,恰好都击中目标2次的概率是

作业
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com