
题目列表(包括答案和解析)
3.证明平面与平面平行的思考途径
(1)转化为判定二平面无公共点;
(2)转化为线面平行;
(3)转化为线面垂直.
2.证明直线与平面的平行的思考途径
(1)转化为直线与平面无公共点;
(2)转化为线线平行;
(3)转化为面面平行.
1..证明直线与直线的平行的思考途径
(1)转化为判定共面二直线无交点;
(2)转化为二直线同与第三条直线平行;
(3)转化为线面平行;
(4)转化为线面垂直;
(5)转化为面面平行.
(1)掌握平面的基本性质,会用斜二测的画法画水平放置的平面图形的直观图.能够画出空间两条直线、直线和平面的各种位置关系的图形.能够根据图形想像它们的位置关系.
(2)掌握两条直线平行与垂直的判定定理和性质定理.掌握两条直线所成的角和距离的概念,对于异面直线的距离,只要求会计算已给出公垂线时的距离.
(3)掌握直线和平面平行的判定定理和性质定理.掌握直线和平面垂直判定定理和性质定理.掌握斜线在平面上的射影、直线和平面所成角、直线和平面的距离的概念.掌握三垂线定理及其逆定理.
(4)掌握两个平面平行的判定定理和性质定理.掌握二面角、二面角平面角、两个平行平面间的距离概念.掌握两个平面垂直的判定定理和性质定理.
(5)会用反证法证明简单的问题.
(6)了解多面体、凸多面体的概念,了解正多面体的概念.
(7)了解棱柱的概念,掌握棱柱的性质
(8)了解棱锥的概念,掌握正棱锥的性质
(9)了解球的概念,掌握球的性质,掌握球的表面积、体积公式.
(三)解答题
15.已知圆锥的侧面展开图是一个半圆,且这个圆锥的体积为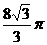 .求圆锥的表面积.
.求圆锥的表面积.
16. 已知PA垂直于正方形ABCD所在的平面,E、F分别是PB和AC的中点,
已知PA垂直于正方形ABCD所在的平面,E、F分别是PB和AC的中点,
求证:①EF//平面PAD;② ;
;
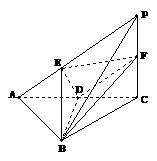 17.已知三棱锥P-ABC中,PC⊥底面ABC,
17.已知三棱锥P-ABC中,PC⊥底面ABC,
AB=BC,D、F分别为AC、PC的中点,DE⊥AP于E.
(1)求证:AP⊥平面BDE;
(2)求证:平面BDE⊥平面BDF;
(3)若AE∶EP=1∶2,求截面BEF分三棱锥P-ABC
所成两部分的体积比.
*18.如图,甲、乙是边长为4a的两块正方形钢
 板,现要将甲裁剪焊接成一个正四棱柱,将乙裁剪焊接成一个正四棱锥,使它们的全面积都等于一个正方形的面积(不计焊接缝的面积)。
板,现要将甲裁剪焊接成一个正四棱柱,将乙裁剪焊接成一个正四棱锥,使它们的全面积都等于一个正方形的面积(不计焊接缝的面积)。
(1)将你的裁剪方法用虚线标示在图中,并作简要说明;
(2)试比较你所制作的正四棱柱与正四棱锥体积的大小,并证明你的结论。
(二)填空题
11.若 ,则直线
,则直线 与AB的位置关系是
.
与AB的位置关系是
.
12.在空间四边形ABCD中,E、F分别是BD、AC的中点,且BC=AD=2EF,则EF与AD所成的角等于 .
13.三棱锥P-ABC中,若棱PA=x,其余各棱长均为1,则x的范围是__________;
三棱锥P-ABC的体积的最大值为__________.
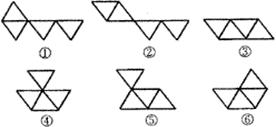
14.下图中,不是正四面体的表面展开图的是____ ___.
(一)选择题
1.下列命题中正确的是( )
A.一条直线与一个点确定一个平面 B.有三个公共点的两个平面必定重合
C.三条直线两两相交,则这三条直线共面
D.若线段AB在平面内,则线段AB延长线上的一点C也在平面内
2.空间三条直线 ,且
,且 ,
, 与
与 相交,则
相交,则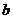 与
与 ( )
( )
A.相交 B.平行 C.异面 D.异面或相交
3.在空间四边形ABCD中,AC=BD,E、F、G、H分别是AB、BC、CD、DA的中点,则四边形EFGH是( )
A.梯形 B.矩形 C.菱形 D.正方形
4.两条异面直线所成的角的范围是( )
A.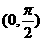 B.
B. C.
C.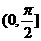 D.
D.
5.平行于棱锥底面的平面把棱锥的高分成 的两部分(自上而下),则截面与棱锥底面的面积之比是(
)
的两部分(自上而下),则截面与棱锥底面的面积之比是(
)
A. B.
B. C.
C. D.
D.
6. 下列命题中,正确的个数是( )
下列命题中,正确的个数是( )
①平行于同一条直线的两直线平行
②平行于同一个平面的两直线平行
③垂直于同一条直线的两直线平行
④垂直于同一个平面的两直线平行
⑤平行于同一条直线的两平面平行
⑥平行于同一个平面的两平面平行
A.1 B.2 C.3 D.4
7.右图是一个几何体的三视图,则这个几何体
的表面积为( )
A.64+16 B.64+32
B.64+32 C.80+16
C.80+16 D.80+32
D.80+32
8.一个底面直径是32cm的圆柱形水箱装入水,
然后放入一个铁球,该球被水淹没,水面升高9cm,则球的表面积是( )
A.144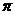 B.288
B.288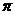 C.576
C.576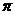 D.2304
D.2304
9.在矩形ABCD中,AB=3,BC=4,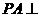 面AC且PA=1,则P到对角线BD的距离是( )
面AC且PA=1,则P到对角线BD的距离是( )
A. B.
B.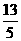 C.
C. D.
D.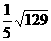
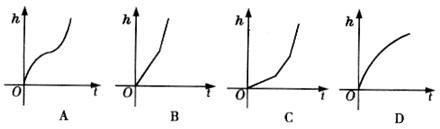
10.从水平放置的球体容器的顶部的一个孔向球内以相同的速度注水,容器中水面的高度与注水时间t之间的关系用图象表示应为( )
1、地位:兵家必争
虽然近年来立体几何试题在命题思路和方法上不时有些出人意外之处,但总体上还是保持了稳定,所以复习备考工作有章可循,有法可依。特别是立体几何试题难度中等,大题分步设问,层次分明,使得不同层次的学生都可得到一定的分数,因而立体几何成为历年数学高考中的“兵家必争之地”。
07考纲(新)对知识的要求依次是了解、理解、掌握三个层次.
(1)了解:要求对所列知识的含义有初步的、感性的认识,知道这一知识内容是什么,按照一定的程序和步骤照样模仿,并能(或会)在有关的问题中识别和认识它.
这一层次所涉及的主要行为动词有:了解,知道、识别,模仿,会求、会解等.
(2)理解:要求对所列知识内容有较深刻的理性认识,知道知识间的逻辑关系,能够对所列知识作正确的描述说明并用数学语言表达,能够利用所学的知识内容对有关问题作比较、判别、讨论,具备利用所学知识解决简单问题的能力.
这一层次所涉及的主要行为动词有:描述,说明,表达,推测、想像,比较、判别,初步应用等.
(3)掌握:要求能够对所列的知识内容推导证明,能够利用所学知识对问题能够进行分析、研究、讨论,并且加以解决.
这一层次所涉及的主要行为动词有:掌握、导出、分析,推导、证明,研究、讨论、运用、解决问题等.
新旧《考纲》的对比如下:
|
编号 |
07考纲(新) |
06考纲(旧) |
|
1 |
认识柱、锥、台、球及其简单组合体的结构特征. |
掌握棱柱的性质,掌握正棱锥的性质,掌握球的性质,掌握球的表面积、体积公式. |
|
2 |
理解空间直线、平面位置关系的定义,并了解如下可以作为推理依据的公理和定理. |
掌握平面的基本性质,能够画出空间两条直线、直线和平面的各种位置关系的图形,能够根据图形想像它们的位置关系. |
|
3 |
|
掌握三垂线定理及其逆定理. |
|
4 |
|
掌握两条直线所成的角和距离的概念,对于异面直线的距离,只要求会计算已给出公垂线时的距离. |
|
5 |
|
掌握斜线在平面上的射影、直线和平面所成的角、直线和平面的距离的概念. |
|
6 |
|
掌握二面角、二面角的平面角、两平行平面间的距离的概念. |
|
7 |
能够画出简单空间图形(长方体、球、圆柱、圆锥、棱柱等的简易组合)的三视图,能够识别上述的三视图所表示的立体模型. |
|
|
8 |
会用平行投影与中心投影两种方法,画出简单空间图形的三视图与直观图. |
|
此外,整个空间向量部分内容新《考纲》已不作要求.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com