4、直线和平面垂直的判定和性质：

(1)判定：①如果一条直线和一个平面内的两条相交直线都垂直，那么这条直线和这个平面垂直。②两条平行线中有一条直线和一个平面垂直，那么另一条直线也和这个平面垂直。

(2)性质：①如果一条直线和一个平面垂直，那么这条直线和这个平面内所有直线都垂直。②如果两条直线都垂直于同一个平面，那么这两条直线平行。

3、直线与平面平行的判定和性质：

①判定定理：如果平面内一条直线和这个平面平面平行，那么这条直线和这个平面平行；

②面面平行的性质：若两个平面平行，则其中一个平面内的任何直线与另一个平面平行。

性质：如果一条直线和一个平面平行，那么经过这条直线的平面和这个平面相交的交线和这条直线平行。在遇到线面平行时，常需作出过已知直线且与已知平面相交的辅助平面，以便运用线面平行的性质。

2、直线与平面的位置关系：

(1)直线在平面内；

(2)直线与平面相交。其中，如果一条直线和平面内任何一条直线都垂直，那么这条直线和这个平面垂直。注意：任一条直线并不等同于无数条直线；(3)直线与平面平行。其中直线与平面相交、直线与平面平行都叫作直线在平面外。

1.两直线平行的判定：

(1)公理4：平行于同一直线的两直线互相平行；(2)线面平行的性质：如果一条直线和一个平面平行，那么经过这条直线的平面和这个平面相交的交线和这条直线平行；

(3)面面平行的性质：如果两个平行平面同时与第三个平面相交，那么它们的交线平行；

(4)线面垂直的性质：如果两条直线都垂直于同一个平面，那么这两条直线平行。

20．几个定理

19。几个公式

(1).斜三棱柱的体积其中S表示一个侧面的面积，表示侧棱到相对的侧面的距离。该公式对于解决以知侧棱到相对侧面距离和该侧面面积求棱柱体积的问题非常有效。

(2)直棱柱剪截体体积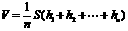巧用

(3)长方体的对角线长的公式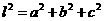

18.空间距离的求法

(1)两异面直线间的距离，高考要求是给出公垂线，一般利用垂直作出公垂线，然后再进行计算；

(2)求点到直线的距离，一般用三垂线定理作出垂线再求解；

(3)求点到平面的距离，

一是用垂面法，借助面面垂直的性质来作，因此，确定已知面的垂面是关键；

二是不作出公垂线，转化为求三棱锥的高，利用等体积法列方程求解；

16.二面角的求法

(1)定义法：直接在二面角的棱上取一点，分别在两个半平面内作棱的垂线，得出平面角，；

(2)三垂线法：已知二面角其中一个面内一点到一个面的垂线，用三垂线定理或逆定理作出二面角的平面角；

(3)垂面法：已知二面角内一点到两个面的垂线时，过两垂线作平面与两个半平面的交线所成的角即为平面角，由此可知，二面角的平面角所在的平面与棱垂直；

(4)射影法：利用面积射影公式S_射＝S_原cos,其中为平面角的大小，此方法不必在图形中画出平面角；

特别:对于一类没有给出棱的二面角，应先延伸两个半平面，使之相交出现棱，然后再选用上述方法(尤其要考虑射影法)。

17直线和平面所成的角：

(1)定义：平面的一条斜线和它在平面内的射影所成的锐角，叫这条直线和这个平面所成的角。

(2)范围：；(3)求法：作出直线在平面上的射影；(4)斜线与平面所成的角的特征：斜线与平面中所有直线所成角中最小的角。

15．经纬度及球面距离

⑴根据经线和纬线的意义可知，某地的经度是一个二面角度数，某地的纬度是一个线面角度数，

⑵两点间的球面距离就是连结球面上两点的大圆的劣弧的长，因此，求两点间的球面距离的关键就在于求出过这两点的球半径的夹角。

14．柱体、锥体的体积

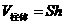(是柱体的底面积、是柱体的高).

(是锥体的底面积、是锥体的高).