
题目列表(包括答案和解析)
4. 直线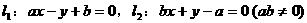 的图象只可能是下图中的( )
的图象只可能是下图中的( )
3. 已知直线 的横截距大于纵截距,则A、B、C应满足的条件是( )
的横截距大于纵截距,则A、B、C应满足的条件是( )
A. A>B B. A<B
C.  D.
D.

2. 过点A(4,1)且在两坐标轴上的截距相等的直线的方程是( )
A. 
B. 
C.  或
或
D.  或
或
1. 直线 与两坐标轴围成的三角形的面积是( )
与两坐标轴围成的三角形的面积是( )
A. 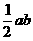 B.
B.  C.
C.  D.
D. 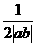
4. 关于直线方程形式间的互化方法。
[典型例题]
例1. 已知直线过点P(-5,-4),且与两坐标轴围成三角形面积为5,求直线l的方程。
解:




例2. 如图,已知直线l经过点P(3,2),且与x轴、y轴的正半轴分别交于点A、B。
(1)求三角形AOB面积的最小值及此时直线l的方程。
(2)求直线l在两坐标轴上的截距之和的最小值及此时直线的方程。

解:(1)法一:设A(0,a),B(b,0)(a>0,b>0)







法二:

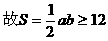

法三:
∵a为实数,∴△≥0



法四:过P分别作x轴、y轴的垂线PM、PN(M、N为垂足),并设θ=∠PAM=∠BPN



(2)法一: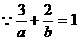
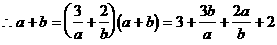
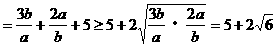
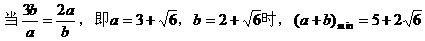
法二:

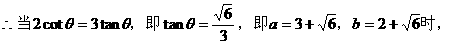
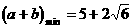
例3. 已知直线mx+ny+12=0在x轴、y轴上的截距分别是-3和4,求m,n的值。
分析:(1)将直线方程化成截距式后(或直接)求出直线在两轴上的截距、解关于m,n的方程组。(2)由已知条件,直线经过点A(-3,0)、B(0,4),由此得m,n的方程组,解之即可。
解法1:由截距意义知,直线经过A(-3,0)和B(0,4)两点,因此有
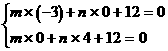

解法2:将方程mx+ny+12=0化为截距式,得:
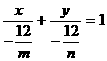


例4. 

解析: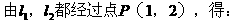
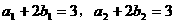


例5. 
距离相等。
分析:(1)设P(x,y),则有y=3x+1,故点P的坐标为(x,3x+1),由距离公式得x的方程,解得x=0。
(2)设P(x,y),求出两点(1,-1),(2,0)的中垂线方程为x+y-1=0,再解方程组得P(0,1)。
解法1:设P(x,y),则有y=3x+1
故点P的坐标为(x,3x+1)
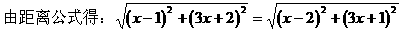
解之得:x=0
∴所求的点为P(0,1)
解法2:设P(x,y),两点(1,-1),(2,0)所连线段的中垂线方程为:


解由<1>、<2>组成的方程组得:P(0,1)
例6. 
(1)证明直线l过定点;
(2)若直线l交x轴负半轴于A,交y轴正半轴于B,△AOB的面积为S,求S的最小值,并求此时直线l的方程;
(3)若直线不经过第四象限,求k的取值范围。
分析:(1)证直线系过定点,可用分离参数法。
(2)求△AOB面积S的最小值,应先求出目标函数S=f(k),再根据目标函数的结构特征选择最小值的求法。
(3)直线不经过第四象限的充要条件是:直线在x轴上的截距小于或等于-2,在y轴上的截距大于或等于1。或由直线经过定点(-2,1)知斜率大于或等于零。
解:(1)直线l的方程是:
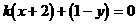

∴无论k取何值,直线总经过定点(-2,1)
(2)由l的方程,得:

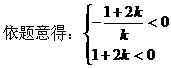
解得:k>0
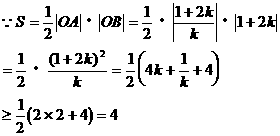


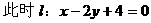
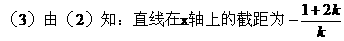


解之得:k>0
小结:本题证明直线系过定点问题所使用的“分离参数法”,也是证明曲线系过定点的一般方法。
例7. 
分析:利用所求直线上任意一点P关于点A的对称点P’在已知直线上的关系求解。
解:设P(x,y)为所求直线上任一点,则:
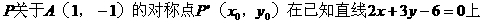

∵线段PP’的中点为A(1,-1)




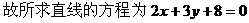
注意:本题是一个关于点对称的直线的求法问题,要注意利用点对称的特点求解。
例8. 一根弹簧挂6公斤的物体时,长11 cm,挂9公斤的物体时,长17 cm。已知弹簧长度l (cm)和所挂物体的重量w(公斤)的关系可以用直线方程来表示。用两点式表示这个方程,并根据这个方程,求弹簧长为13 cm时所挂物体的重量。
解:以Ow为横坐标轴,以Ol为纵坐标轴建立直角坐标系(如图所示)

由题意知直线过点(6,11)和点(9,17)
由直线的两点式方程得所求直线的方程为:


∴w=7
即弹簧长为13 cm时所挂物体的重量为7公斤。
小结:因为弹簧长l和所挂物体的重量w的关系可以用直线方程来表示,并且弹簧挂6公斤的物体时,长11 cm;弹簧挂9公斤的物体时,长17 cm。所以直线过点(6,11)和(9,17)。由直线方程的两点式求出l、w关系,得解。
例9. 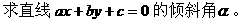
解:





小结:由直线方程的一般式求直线的倾斜角时,须先求其斜率,这时通常把直线方程化成斜截式(若直线没有斜率即y的系数为0,则直线的倾斜角为90°,此时直线方程没有斜截式),然后根据斜率再求直线的倾斜角。当直线的斜率k≥0时,直线的倾斜角为arctank;当直线的斜率k<0时,直线的倾斜角为π+arctank。
例10. 

证明:如图所示,过P(x1,y1)作直线垂直于x轴,交直线l于M

设M点的坐标为(x1,y2),则:
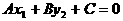
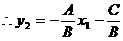
∵P在M的上方
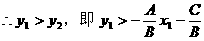


小结: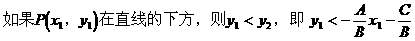

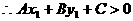
点P在直线的上方或下方就是指在同横坐标时,P的纵坐标大于或小于直线上的点对应的纵坐标。
[模拟试题]
3. 直线方程的一般式:
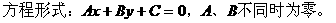
适用范围:平面直角坐标系中,任何一条直线都可由一般式表示出来。
2. 直线方程的截距式:
公式推导:已知直线与x轴交于A(0,a)与y轴交于B(b,0),其中(a≠0,b≠0)求直线l的方程。



注意:(1)特殊情况:当a=0或b=0时不能用上式,即过原点或与x轴平行或与y轴平行的直线不能用截距式。
(2)截距式是两点式的特殊情况。
直线方程
[知识点]
1. 直线方程两点式:

方程?
解:



注意:(1)特殊情况:x=x1或y=y1不能用两点式表示,即与x轴平行或与x轴垂直的直线不能用两点式表示,故平面上的直线与两点式方程不是一一对应。
(2)两点式变形形式:(y-y1)(x2-x1)=(y2-y1)(x-x1)
此方程与平面上的直线一一对应。
3. 过点P(4,2)作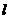 分别交
分别交 轴,
轴, 轴正半轴于A、B两点,当
轴正半轴于A、B两点,当 面积最小时,求直线
面积最小时,求直线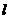 的方程。
的方程。
2. 已知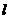 与
与 的倾斜角相等,且与两坐标轴围成的三角形的面积为24,求
的倾斜角相等,且与两坐标轴围成的三角形的面积为24,求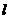 的方程。
的方程。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com