
题目列表(包括答案和解析)
1 从甲、乙,……,等
从甲、乙,……,等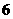 人中选出
人中选出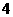 名代表,那么(1)甲一定当选,共有
种选法
名代表,那么(1)甲一定当选,共有
种选法 (2)甲一定不入选,共有 种选法
(2)甲一定不入选,共有 种选法 (3)甲、乙二人至少有一人当选,共有 种选法
(3)甲、乙二人至少有一人当选,共有 种选法
2
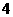 名男生,
名男生,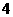 名女生排成一排,女生不排两端,则有 种不同排法
名女生排成一排,女生不排两端,则有 种不同排法
3 由
由 这六个数字组成_____个没有重复数字的六位奇数
这六个数字组成_____个没有重复数字的六位奇数
4 在
在 的展开式中,
的展开式中, 的系数是
的系数是 
5 在
在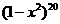 展开式中,如果第
展开式中,如果第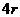 项和第
项和第 项的二项式系数相等,
项的二项式系数相等,
则 ,
,

6 在
在 的九个数字里,任取四个数字排成一个首末两个数字是奇数的四位数,这样的四位数有_________________个?
的九个数字里,任取四个数字排成一个首末两个数字是奇数的四位数,这样的四位数有_________________个?
7 用
用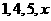 四个不同数字组成四位数,所有这些四位数中的数字的总和为
四个不同数字组成四位数,所有这些四位数中的数字的总和为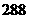 ,则
,则

8 从
从 中任取三个数字,从
中任取三个数字,从 中任取两个数字,组成没有重复数字的五位数,共有________________个?
中任取两个数字,组成没有重复数字的五位数,共有________________个?
1 将
将 个不同的小球放入
个不同的小球放入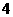 个盒子中,则不同放法种数有( )
个盒子中,则不同放法种数有( )
A
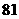 B
B
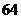 C
C
 D
D

2 从
从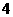 台甲型和
台甲型和 台乙型电视机中任意取出
台乙型电视机中任意取出 台,其中至少有甲型与乙型电视机各
台,其中至少有甲型与乙型电视机各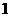 台,则不同的取法共有( )
台,则不同的取法共有( )
A
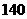 种 B
种 B
 种 C
种 C
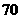 种 D
种 D
 种
种
3
 个人排成一排,其中甲、乙两人至少有一人在两端的排法种数有(
)
个人排成一排,其中甲、乙两人至少有一人在两端的排法种数有(
)
A
 B
B
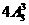 C
C
 D
D

4
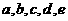 共
共 个人,从中选1名组长1名副组长,但
个人,从中选1名组长1名副组长,但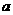 不能当副组长,不同的选法总数是( )
不能当副组长,不同的选法总数是( )
A
 B
B
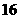 C
C
 D
D
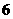
5 现有男、女学生共
现有男、女学生共 人,从男生中选
人,从男生中选 人,从女生中选
人,从女生中选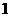 人分别参加数学、物理、化学三科竞赛,共有
人分别参加数学、物理、化学三科竞赛,共有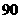 种不同方案,那么男、女生人数分别是( )
种不同方案,那么男、女生人数分别是( )
A 男生
男生 人,女生
人,女生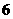 人
B
人
B 男生
男生 人,女生
人,女生 人
人
C 男生
男生 人,女生
人,女生 人
D
人
D 男生
男生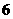 人,女生
人,女生 人
人
6 在
在 的展开式中的常数项是( )
的展开式中的常数项是( )
A
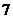 B
B
 C
C
 D
D
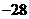
7
 的展开式中
的展开式中 的项的系数是( )
的项的系数是( )
A
 B
B
 C
C
 D
D

8
 展开式中只有第六项二项式系数最大,则展开式中的常数项是( )
展开式中只有第六项二项式系数最大,则展开式中的常数项是( )
A
 B
B
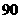 C
C
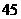 D
D

1
 个人坐在一排
个人坐在一排 个座位上,问(1)空位不相邻的坐法有多少种?(2)
个座位上,问(1)空位不相邻的坐法有多少种?(2) 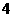 个空位只有
个空位只有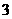 个相邻的坐法有多少种?(3)
个相邻的坐法有多少种?(3) 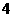 个空位至多有
个空位至多有 个相邻的坐法有多少种?
个相邻的坐法有多少种?
2 有
有 个球,其中
个球,其中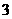 个黑球,红、白、蓝球各
个黑球,红、白、蓝球各 个,现从中取出
个,现从中取出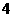 个球排成一列,共有多少种不同的排法?
个球排成一列,共有多少种不同的排法?
3 求
求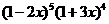 展开式中按
展开式中按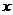 的降幂排列的前两项
的降幂排列的前两项
4 用二项式定理证明:
用二项式定理证明: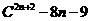 能被
能被 整除
整除

5 求证:
求证:

6 (1)若
(1)若 的展开式中,
的展开式中, 的系数是
的系数是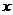 的系数的
的系数的 倍,求
倍,求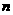 ;
;
(2)已知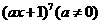 的展开式中,
的展开式中,  的系数是
的系数是 的系数与
的系数与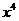 的系数的等差中项,求
的系数的等差中项,求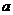 ;
;
(3)已知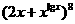 的展开式中,二项式系数最大的项的值等于
的展开式中,二项式系数最大的项的值等于 ,求
,求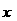

1 将数字
将数字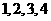 填入标号为
填入标号为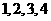 的四个方格里,每格填一个数字,则每个方格的标号与所填的数字均不同的填法有 种?
的四个方格里,每格填一个数字,则每个方格的标号与所填的数字均不同的填法有 种?
2 在△
在△ 的边
的边 上有
上有 个点,边
个点,边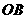 上有
上有 个点,加上
个点,加上 点共个点,以这
点共个点,以这 个点为顶点的三角形有 个
个点为顶点的三角形有 个
3 从
从 ,
,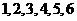 这七个数字中任取三个不同数字作为二次函数
这七个数字中任取三个不同数字作为二次函数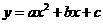 的系数
的系数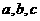 则可组成不同的函数_______个,其中以
则可组成不同的函数_______个,其中以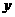 轴作为该函数的图像的对称轴的函数有______个
轴作为该函数的图像的对称轴的函数有______个
4 若
若 的展开式中
的展开式中 的系数为
的系数为 ,则常数
,则常数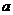 的值为
的值为 
5 若
若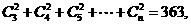 则自然数
则自然数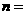 _____
_____
6 若
若 ,则
,则

7
 的近似值(精确到
的近似值(精确到 )是多少?
)是多少?
8 已知
已知 ,那么
,那么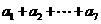 等于多少?
等于多少?
1 若
若 ,则
,则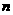 的值为( )
的值为( )
A
 B
B
 C
C
 D
D
2 某班有
某班有 名男生,
名男生, 名女生,现要从中选出
名女生,现要从中选出 人组成一个宣传小组,
人组成一个宣传小组,
其中男、女学生均不少于 人的选法为( )
人的选法为( )
A
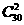
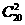
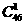 B
B

C
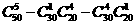 D
D

3
 本不同的书分给甲、乙、丙三人,每人两本,不同的分法种数是( )
本不同的书分给甲、乙、丙三人,每人两本,不同的分法种数是( )
A
 B
B
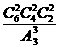 C
C
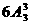 D
D
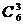
4 设含有
设含有 个元素的集合的全部子集数为
个元素的集合的全部子集数为 ,其中由
,其中由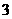 个元素组成的子集数为
个元素组成的子集数为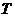 ,则
,则 的值为( )
的值为( )
A
 B
B
 C
C
 D
D

5 若
若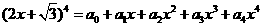 ,则
,则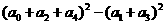 的值为( )
的值为( )
A
 B
B
 C
C
 D
D

6 在
在 的展开式中,若第七项系数最大,则
的展开式中,若第七项系数最大,则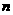 的值可能等于( )
的值可能等于( )
A
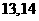 B
B
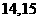 C
C
 D
D
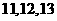
7 不共面的四个定点到平面
不共面的四个定点到平面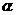 的距离都相等,这样的平面
的距离都相等,这样的平面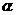 共有( )
共有( )
A
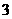 个 B
个 B
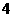 个
个
C
 个 D
个 D
 个
个
8 由
由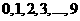 十个数码和一个虚数单位
十个数码和一个虚数单位 可以组成虚数的个数为( )
可以组成虚数的个数为( )
A
 B
B
 C
C
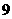 D
D

1 集合
集合 中有
中有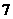 个元素,集合
个元素,集合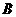 中有
中有 个元素,集合
个元素,集合
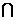
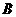 中有
中有 个元素,集合
个元素,集合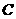 满足
满足
(1)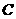 有
有 个元素; (2)
个元素; (2)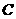



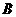
(3)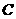
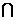
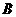

 ,
, 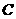
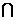


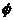 求这样的集合
求这样的集合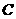 的集合个数
的集合个数
2 计算:(1)
计算:(1)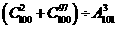 ;
;
(2)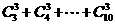

(3)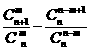
3 证明:
证明:

4 求
求 展开式中的常数项
展开式中的常数项
5 从
从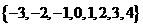 中任选三个不同元素作为二次函数
中任选三个不同元素作为二次函数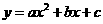 的系数,问能组成多少条图像为经过原点且顶点在第一象限或第三象限的抛物线?
的系数,问能组成多少条图像为经过原点且顶点在第一象限或第三象限的抛物线?
6
 张椅子排成,有
张椅子排成,有 个人就座,每人
个人就座,每人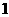 个座位,恰有
个座位,恰有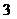 个连续空位的坐法共有多少种?
个连续空位的坐法共有多少种?
1
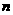 个人参加某项资格考试,能否通过,有 种可能的结果?
个人参加某项资格考试,能否通过,有 种可能的结果?
2 以
以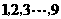 这几个数中任取
这几个数中任取 个数,使它们的和为奇数,则共有 种不同取法
个数,使它们的和为奇数,则共有 种不同取法
3 已知集合
已知集合 ,
, ,从集合
,从集合 ,
,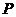 中各取一个元素作为点的坐标,可作出不同的点共有_____个
中各取一个元素作为点的坐标,可作出不同的点共有_____个
4
 且
且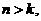 若
若 则
则 ______
______
5
 展开式中的常数项有
展开式中的常数项有
6 在
在 件产品
件产品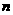 中有
中有 件是次品,从中任意抽了
件是次品,从中任意抽了 件,至少有
件,至少有 件是次品的抽法共有______________种(用数字作答)
件是次品的抽法共有______________种(用数字作答)
7
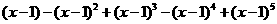 的展开式中的
的展开式中的 的系数是___________
的系数是___________
8
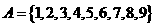 ,则含有五个元素,且其中至少有两个偶数的子集个数为_____
,则含有五个元素,且其中至少有两个偶数的子集个数为_____
1 由数字
由数字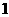 、
、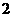 、
、 、
、 、
、 组成没有重复数字的五位数,其中小于
组成没有重复数字的五位数,其中小于 的偶数共有( )
的偶数共有( )
A
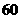 个 B
个 B
 个 C
个 C
 个 D
个 D
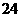 个
个
2
 张不同的电影票全部分给
张不同的电影票全部分给 个人,每人至多一张,则有不同分法的种数是( )
个人,每人至多一张,则有不同分法的种数是( )
A
 B
B
 C
C
 D
D

3
 且
且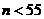 ,则乘积
,则乘积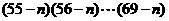 等于
等于
A
 B
B
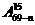 C
C
 D
D

4 从字母
从字母 中选出4个数字排成一列,其中一定要选出
中选出4个数字排成一列,其中一定要选出 和
和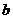 ,并且必须相邻(
,并且必须相邻( 在
在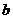 的前面),共有排列方法( )种
的前面),共有排列方法( )种
A
 B
B
 C
C
 D
D

5 从不同号码的
从不同号码的 双鞋中任取
双鞋中任取 只,其中恰好有
只,其中恰好有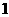 双的取法种数为( )
双的取法种数为( )
A
 B
B
 C
C
 D
D
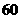
6 把
把 按照二项式定理来展开,则展开式的第
按照二项式定理来展开,则展开式的第 项的系数是( )
项的系数是( )
A
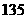 B
B
 C
C
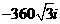 D
D

7 在
在 的展开式中,
的展开式中, 的系数是
的系数是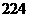 ,则
,则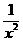 的系数是( )
的系数是( )
A
 B
B
 C
C
 D
D

8 在
在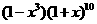 的展开中,
的展开中, 的系数是( )
的系数是( )
A
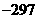 B
B
 C
C
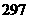 D
D

22、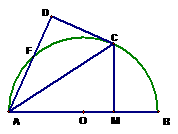 A、选修4-1:几何证明选讲
A、选修4-1:几何证明选讲
如图,AB是⊙O的直径,C、F为⊙O上的点,CA是∠BAF的角平分线,过点C作CD⊥AF交AF的延长线于D点,CM⊥AB,垂足为点M。(1)求证:DC是⊙O的切线;(2)求证:AM·MB=DF·DA。
B、选修4-4:坐标系与参数方程
已知圆锥曲线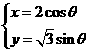 (
( 是参数)和定点A(0,
是参数)和定点A(0,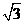 ),F1、F2是圆锥曲线的左、右焦点。
),F1、F2是圆锥曲线的左、右焦点。
(1)求经过点F1垂直于直线AF2的直线l的参数方程;(2)以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,求直线AF2的极坐标方程。
 。
。
21、已知数列{an}的前n项和为Sn,函数 (其中p、q均为常数,且p>q>0),当x=a1时,函数f(x)取得极小值,点(n,2Sn)(n∈N*)均在函数
(其中p、q均为常数,且p>q>0),当x=a1时,函数f(x)取得极小值,点(n,2Sn)(n∈N*)均在函数 的图象上(其中是
的图象上(其中是 函数f(x)的导函数)。
函数f(x)的导函数)。
(1)求a1的值;(2)求数列{an}的通项公式;(3)记 ·
· ,求数列{bn}的前n项和Tn。
,求数列{bn}的前n项和Tn。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com