
题目列表(包括答案和解析)
[例1]原市话资费为每3分钟0.18元,现调整为前3分钟资费为0.22元,超过3分钟的,每分钟按0.11元计算,与调整前相比,一次通话提价的百分率( )
A.不会提高70% B.会高于70%,但不会高于90%
C.不会低于10% D.高于30%,但低于100%
[小题大做]设一次通话时间为x分钟,调整前话费为S1元,调整后话费为S2元,提价的百分率为y,则y = ·100%,列表如下(时间包尾计算):
|
x范围 (n∈N+) |
S1 |
S2 |
y |
x∈ |
0.18 |
0.22 |
22.2% |
x∈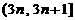 |
0.18n+0.18 |
0.22+0.11[(3n+1)-3]=0.33n |
·100% |
x∈ |
0.18n+0.18 |
0.22+0.11[(3n+2)-3]=0.33n+0.11 |
·100% |
x∈ |
0.18n+0.18 |
0.22+0.11[(3n+3)-3]=0.33n+0.22 |
·100% |
根据表中计算结果:y < ·100%≈83.3%,取n=1,对应于y = -8.3%、22.2%、50.8%,故排除A、C、D,选B。
[小结]这里运用了分类讨论和表格,进行建模、计算、排除,若是一道解答题,这样做是再好不过,遗憾的是选择题,那如何“巧”做呢?!
[特殊值法]取x=4,y=·100%≈-8.3%,排除C、D;取x=30,
y = ·100%≈77.2%,排除A,从而选B。
『类题1』 设 = , p = (x1 -)2+ (x2 -)2+…+ (xn -)2,
q = (x1- a)2+ (x2 -a)2+…+ (xn -a)2,若 ≠a,则一定有( )
A.p>q B.p=q C.p<q D.与a的值有关
特殊化,n =1,p =0,q >0,选C,此为方差最小原理,如何证明?
『类题2』在 ABC中,角A、B、C所对的边分别为a、b、c,如果a、b、c成等差数列,则
ABC中,角A、B、C所对的边分别为a、b、c,如果a、b、c成等差数列,则
法一:取a=3, b=4, c=5 ,则cosA= cosC=0,
cosC=0, 

法二:取A=B=C=600 cosA=cosC= ,
,

『类题3』过抛物线y=ax2 (a>0) 的焦点F作一直线交抛物线于P、Q 两点,如果线段PF与FQ的长分别是p、q,则
A、2a B、 C、4a
D、
C、4a
D、
法一:取特殊情况,PQ∥x轴, ,选C
,选C
法二: 取特殊情况,PQ∥y轴, , 选C
, 选C
[例2]以双曲线 的左焦点F,左准线l为相应的焦点和准线的椭圆截直线y=kx+3所得的弦恰好被x轴平分,则k的取值范围是 。
[小题大做]F(-2,0),l:x =- ,可设椭圆 (a>b>0),与直线y=kx+3联立,消去y得:(b2+a2k2)x2 -2(b2x0-3a2k)x+9a2-a2b2 = 0,△>0时得 = ,又直线y=kx+3与x轴交于点(- ,0),据题设知:- =,解得x0 =- ,而椭圆中心O1(x0,0)在右焦点F的左侧,∴x0 =- <-2,解得0<k<。
[小结]若简缩思维,抓住问题的本质:直线与x轴的交点--弦的中点--椭圆的中心(为 什么?),你有哪些科学的解法?
什么?),你有哪些科学的解法?
[解法一](特征分析法):F(-2,0),
l:x =-,根据椭圆的对称性知椭圆中心
O1(- ,0),又- < -2,得0 < k < 。
[解法二]作出椭圆(草图),注意到直线y=kx+3过定点M(0,3)及椭圆中心O1,
知kOM=k∈(0,)。
『类题1』设球的半径为R, P、Q是球面上北纬600圈上的两点,这两点在纬度圈上的劣弧的长是 ,则这两点的球面距离是( )
,则这两点的球面距离是( )
A、 B、
B、 C、
C、 D、
D、
分析:纬线弧长>球面距离>直线距离,排除A、B、D,选C
『类题2』sin2180+sin2540= ( )
A、1
B、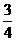 C、
C、 D、
D、
分析: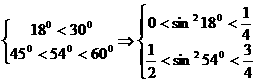 ,选B
,选B
『类题3』 ,记数列{an}的前n项和为Sn,则使得Sn>0的最小正整数n的值是( )
,记数列{an}的前n项和为Sn,则使得Sn>0的最小正整数n的值是( )
A、10 B、11 C、12 D、5
分析: 的图象关于点(5.5,0)对称,S10=0,选B
的图象关于点(5.5,0)对称,S10=0,选B
20.解(1)由抛物线的光学性质及题意知光线PQ必过抛物线的焦点 ,设
,设 ,代入抛物线方程得:
,代入抛物线方程得: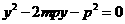 ,
, (6分)
(6分)
(2)设 ,由题意知
,由题意知 ,又设
,又设 是点M关于直线l的对称点,则有:
是点M关于直线l的对称点,则有: ,
,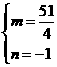 ,
,
由对称性质知 ,代入直线l的方程得
,代入直线l的方程得 (或利用到角公式得
(或利用到角公式得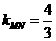 ,求出
,求出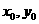 )。由
)。由 ,则
,则 ,又P,F,Q三点共线得P=2。抛物线方程为
,又P,F,Q三点共线得P=2。抛物线方程为 。(14分)
。(14分)
20. 抛物线有光学性质,即由其焦点射出的光线经抛物线反射后,沿平行于抛物线对称轴的方向射出,如右图所示,今有抛物线
抛物线有光学性质,即由其焦点射出的光线经抛物线反射后,沿平行于抛物线对称轴的方向射出,如右图所示,今有抛物线 ,一光源在点
,一光源在点 处,由其发出的光线沿平行于抛物线的轴的方向射向抛物线上的点P,反射后,又射向抛物线上的点Q,再反射后又沿平行于抛物线的轴的方向射出,途中遇到直线
处,由其发出的光线沿平行于抛物线的轴的方向射向抛物线上的点P,反射后,又射向抛物线上的点Q,再反射后又沿平行于抛物线的轴的方向射出,途中遇到直线 上的点N,再反射后又射回点M。
上的点N,再反射后又射回点M。
(1)设P、Q两点的坐标分别是 ,
,
证明: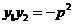 。
。
(2)求抛物线方程。(14分)
22.(1)∵,∴tanθ=.
又∵<m<4,∴1<m<4.………………………………6分
(2)设所求的双曲线方程为(a>0,b>0),Q(x1,y1),
则=(x1-c,y1),∴S△OFQ= ||·|y1|=2,∴y1=±.
又由·=(c,0)·(x1-c,y1)=(x1-c)c=(-1)c2,∴x1=c.…………8分
∴||==≥.
当且仅当c=4时, ||最小,这时Q点的坐标为(,)或(,-).……12分
∴, ∴.
故所求的双曲双曲线方程为
22. 已知ΔOFQ的面积为2,且·=m .
(1)设<m<4,求向量与的夹角θ正切值的取值范围;
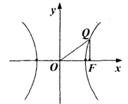 (2)设以O为中心,F为焦点的双曲线经过点Q(如图),||=c,m=(-1)c2,当||取得最小值时,求此双曲线的方程.(本题满分14分)
(2)设以O为中心,F为焦点的双曲线经过点Q(如图),||=c,m=(-1)c2,当||取得最小值时,求此双曲线的方程.(本题满分14分)
22.
 解:(1)
解:(1)

 故
故 (6分)
(6分)
(2)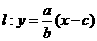 联立
联立 得
得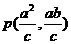 (8分)
(8分)
设A分 的比为
的比为 ,则A
,则A
代入 ,整理化简得:
,整理化简得: (12分)
(12分)
 即
即 的最大值为
的最大值为
(18)本小题满分14分





圆中,求面积最小的圆的半径长。
(18)解: ………………1分
………………1分

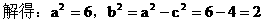 ………………3分
………………3分
 ………………4分
………………4分

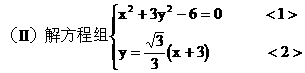
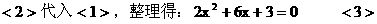 …………6分
…………6分

 ………………7分
………………7分


 ………………11分
………………11分

 ………………12分
………………12分
(III)面积最小的圆的半径应是点F到直线l的距离,设为r………………13分
 ………………14分
………………14分

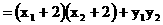





22.(本小题满分14分)已知椭圆C的方程为 ,双曲线
,双曲线 的两条渐近线为
的两条渐近线为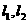 ,过椭圆C的右焦点F的直线
,过椭圆C的右焦点F的直线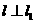 ,又
,又 与
与 交于P点,设
交于P点,设 与椭圆C的两个交点由上至下依次为A,B.
与椭圆C的两个交点由上至下依次为A,B.
(1) 当 与
与 夹角为
夹角为 且
且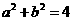 时,求椭圆C的方程.
时,求椭圆C的方程.
(2) 求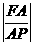 的最大值.
的最大值.
23. 解:(Ⅰ)
直线 方程为
方程为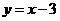 ,设点
,设点 ,
,
由
及 ,得
,得 ,
,
∴点 的坐标为
的坐标为
(Ⅱ)由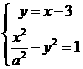 得
得 ,
,
设 ,则
,则 ,得
,得 ,
,
此时, ,∴
,∴ 。
。
23.(14分)已知倾斜角为 的直线
的直线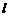 过点
过点 和点
和点 ,其中
,其中 在第一象限,且
在第一象限,且
(Ⅰ)求点 的坐标;
的坐标;
(Ⅱ)若直线 与双曲线
与双曲线
 相交于不同的两点
相交于不同的两点 ,且线段
,且线段 的中点坐标为
的中点坐标为 ,求实数
,求实数 的值。
的值。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com