
题目列表(包括答案和解析)
19、(本小题满分14分)设函数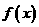
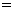

 为奇函数,
为奇函数,
又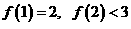 ,且
,且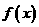 在
在 上递增。
上递增。
⑴ 求 、
、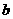 、
、 的值; ⑵ 当
的值; ⑵ 当 时,讨论
时,讨论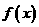 的单调性.
的单调性.
18、(本小题满分14分)某厂家拟在2007年举行促销活动,经调查测算,该产品的年销售量(即该厂的年产量) 万件与年促销费用
万件与年促销费用 万元(
万元( (
( 为常数),如果不搞促销活动,则该产品的年销售量只能是1万件。已知2004年生产该产品的固定投入为8万元,每生产1万件该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品年平均成本的1.5倍(产品成本包括固定投入和再投入两部分资金)。
为常数),如果不搞促销活动,则该产品的年销售量只能是1万件。已知2004年生产该产品的固定投入为8万元,每生产1万件该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品年平均成本的1.5倍(产品成本包括固定投入和再投入两部分资金)。
⑴ 将2007年该产品的利润y万元表示为年促销费用 万元的函数;
万元的函数;
⑵ 该厂家2007年的促销费用投入多少万元时,厂家的利润最大?
17、(本小题12分)已知函数

⑴ 判断函数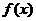 的奇偶性,并证明之;
的奇偶性,并证明之;
⑵ 求函数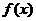 的单调递减区间。
的单调递减区间。
16、(本小题12分) 已知函数 ,当x = 1时,
,当x = 1时,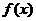 有极大值3.
有极大值3.
⑴ 求 ,
,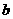 的值;
的值;
⑵ 求函数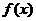 在
在 上的最小值.
上的最小值.
15、(本小题12分)已知命题P: 有两实数根;命题Q:函数
有两实数根;命题Q:函数 上为增函数。若命题P
上为增函数。若命题P Q为假命题,P
Q为假命题,P Q为真命题,求实数
Q为真命题,求实数 的取值范围。
的取值范围。
14、 有一面足够长的墙,现用一36米长的篱笆围成如图所示的四个面积相等的猪圈,那么猪圈的最大总面积为
.
有一面足够长的墙,现用一36米长的篱笆围成如图所示的四个面积相等的猪圈,那么猪圈的最大总面积为
.
13、已知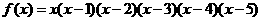 , 则
, 则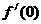 =_____________
=_____________
12、命题“若 ,则
,则 、
、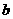 中至少有一个为零”的逆否命题为
中至少有一个为零”的逆否命题为
.
11、方程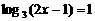 的解
的解 .
.
10、定义新运算 :当
:当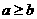 时,
时, ;当
;当 时,
时,  ,则函数
,则函数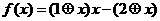 ,
, 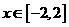 的最大值等于( )
的最大值等于( )
(A) -1 (B) 1 (C) 6 (D) 12
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com