
题目列表(包括答案和解析)
21.(本小题满分14分)
已知二次函数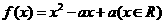 同时满足:①不等式
同时满足:①不等式 ≤0的解集有且只有一个元素;②在定义域内存在
≤0的解集有且只有一个元素;②在定义域内存在 ,使得不等式
,使得不等式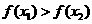 成立,设数列{
成立,设数列{ }的前
}的前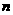 项和
项和 .
.
(1)求函数 的表达式;
的表达式;
(2) 设各项均不为0的数列{ }中,所有满足
}中,所有满足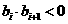 的整数
的整数 的个数称为这个数列{
的个数称为这个数列{ }的变号数,令
}的变号数,令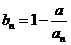 (
(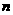
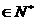 ),求数列{
),求数列{ }的变号数; []
}的变号数; []
(3)设数列{ }满足:
}满足: ,试探究数列{
,试探究数列{ }是否存在最小项?若存在,求出该项,若不存在,说明理由.
}是否存在最小项?若存在,求出该项,若不存在,说明理由.
20.(本小题满分14分)
设直线 与椭圆
与椭圆 相交于A、B两个不同的点,与x轴相交于点C,记O为坐标原点.
相交于A、B两个不同的点,与x轴相交于点C,记O为坐标原点.
(1)证明: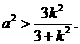 ;
;
(2)若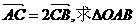 的面积取得最大值时的椭圆方程.
的面积取得最大值时的椭圆方程.
19.(本小题满分13分)
为迎接2008年奥运会召开,某工艺品加工厂准备生产具有收藏价值的奥运会标志--“中国印·舞动的北京”和奥运会吉祥物--“福娃”.该厂所用的主要原料为A、B两种贵重金属,已知生产一套奥运会标志需用原料A和原料B的量分别为4盒和3盒,生产一套奥运会吉祥物需用原料A和原料B的量分别为5盒和10盒.若奥运会标志每套可获利700元,奥运会吉祥物每套可获利1200元,该厂月初一次性购进原料A、B的量分别为200盒和300盒.问该厂生产奥运会标志和奥运会吉祥物各多少套才能使该厂月利润最大,最大利润为多少?
18.(本小题满分14分)
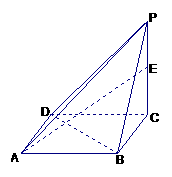
已知一四棱锥P-ABCD的三视图如下,E是侧棱PC上的动点。
(1)求四棱锥P-ABCD的体积;
(2)是否不论点E在何位置,都有BD⊥AE?证明你的结论;
(3)若点E为PC的中点,求二面角D-AE-B的大小.

17.(本小题满分13分)[]
已知函数
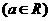 ,函数
,函数
(1)判断方程 的零点个数;
的零点个数;
(2)解关于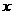 的不等式
的不等式 ,并用程序框图表示你的求解过程.
,并用程序框图表示你的求解过程.
16.(本小题满分12分)
已知:向量 ,
,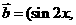
 ,函数
,函数
(1)若 且
且
 ,求
,求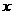 的值;
的值;
(2)求函数 的单调增区间以及函数取得最大值时,向量
的单调增区间以及函数取得最大值时,向量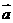 与
与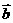 的夹角.
的夹角.
15.(坐标系与参数方程选做题) 在极坐标系中,已知直线过点(1,0),且其向上的方向与极轴的正方向所成的最小正角为 ,则直线的极坐标方程为______________.
,则直线的极坐标方程为______________.
14. (不等式选讲选做题) 函数y= 的最大值为
.
的最大值为
.
13. (几何证明选讲选做题) 如图,
(几何证明选讲选做题) 如图, 是半圆
是半圆 的直径,点
的直径,点 在半圆上,
在半圆上,
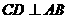 于点
于点 ,且
,且 ,设
,设 ,则
,则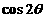 = .
= .
12.某中学号召学生在暑假期间至少参加一次社会公益活动(以下简
称活动).该校文学社共有100名学生,他们参加活动的次数统计如
右图所示.则该文学社学生参加活动的人均次数为 ;从文学
社中任意选两名学生,他们参加活动次数不同的概率是 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com