
题目列表(包括答案和解析)
23.(本题满分14分)
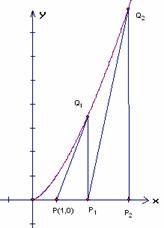 如图,过点P(1,0)作曲线C:
如图,过点P(1,0)作曲线C: 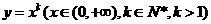 的切线,切点为
的切线,切点为 ,设
,设 点在x轴上的投影是点
点在x轴上的投影是点 ;又过点
;又过点 作曲线C的切线,切点为
作曲线C的切线,切点为 ,设
,设 在x轴上的投影是
在x轴上的投影是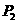 ;…;依此下去,得到一系列点
;…;依此下去,得到一系列点 ,
, ,…,
,…, ,…,设点
,…,设点 的横坐标为
的横坐标为 .
.
(Ⅰ)试求数列{ }的通项公式
}的通项公式 ;(用
;(用 的代数式表示)
的代数式表示)
(Ⅱ)求证:
(Ⅲ)求证: (注:
(注: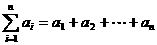 ).
).
22.(本题满分14分)已知=(c,0)(c>0), =(n,n)(n∈R), ||的最小值为1,若动点P同时满足下列三个条件:
①|| = ||(a>c>0);
② = (其中=(,t),
(其中=(,t), ≠0,t∈R);
≠0,t∈R);
③动点P的轨迹C经过点B(0,-1) .
(Ⅰ)求c的值;
(Ⅱ)求曲线C的方程;
(Ⅲ)是否存在方向向量为a=(1,k)(k≠0)的直线l,使l与曲线C交于两个不同的点M、N,且||=||?若存在,求出k的范围;若不存在,请说明理由.
21.(本题满分14分)
如图,已知正方形ABCD和矩形ACEF所在平面互相垂直,
 AB=
AB= ,AF=1,M是线段EF的中点。
,AF=1,M是线段EF的中点。
(Ⅰ)求证:AM∥平面BDE;
(Ⅱ) 求二面角A-DF-B的大小.
(Ⅲ)试问:在线段AC上是否存在一点P,使得直线PF与AD所成角为60°?
20.(本小题满分12分)
甲、乙两人在一场五局三胜制的象棋比赛中,规定甲或乙无论谁先赢满三局就获胜,并且比赛就此结束.现已知甲、乙两人每比赛一局甲取胜的概率是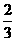 ,乙取胜的概率为
,乙取胜的概率为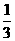 ,且每局比赛的胜负是独立的,试求下列问题:
,且每局比赛的胜负是独立的,试求下列问题:
(Ⅰ)比赛以甲3胜1而结束的概率;
(Ⅱ)比赛以乙3胜2而结束的概率;
(Ⅲ)设甲获胜的概率为a,乙获胜的概率为b,求a:b的值.
19.(本题满分12分)
已知向量 (
( ) 和
) 和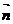 =(
=( ),
),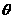 ∈[π,2π].
∈[π,2π].
(Ⅰ)求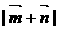 的最大值;(Ⅱ)当
的最大值;(Ⅱ)当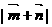 =
=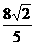 时,求
时,求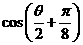 的值.
的值.
17.如图,在杨辉三角中,斜线l上方,从1开始箭头所示的数组成一个锯齿数列:1,3,3,4,6,5,10,…,记其前n项和为Sn,则S19等于____________.
1
1 1 l
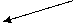 1 2 1
1 2 1

 1 3 3 1
1 3 3 1

 1 4 6 4 1
1 4 6 4 1

 1 5 10 10 5 1
1 5 10 10 5 1
… … … … … … …
 18. 已知f(x+y)=f(x)·f(y)对任意的实数x、y都成立,且f(1)=2,则+++…++=
___________________.
18. 已知f(x+y)=f(x)·f(y)对任意的实数x、y都成立,且f(1)=2,则+++…++=
___________________.
16.若函数 满足:对于任意
满足:对于任意 都有
都有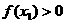 ,
, 且
且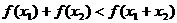 成立,则称函数
成立,则称函数 具有性质M.
具有性质M.
给出下列四个函数:① ,②
,②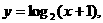 ③
③ ,④
,④ .
.
其中具有性质M的函数是 (注:把满足题意的所有函数的序号都填上)
15. 已知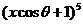 的展开式中
的展开式中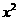 的系数与
的系数与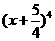 的展开式中
的展开式中 的系数相等,则
的系数相等,则 =_____________.
=_____________.
14. 设点P是曲线y=x3-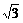 x+2上的任意一点,P点处切线倾斜角为α,则角α的取值范围是______________
x+2上的任意一点,P点处切线倾斜角为α,则角α的取值范围是______________
13.已知函数f(x)=Acos2(ωx+ )+1(A>0,ω>0)的最大值为3,f(x)的图象在y轴上的截距为2,其相邻两对称轴间的距离为2,则f(1)+f(2)+f(3)+…+f(100)=____________
)+1(A>0,ω>0)的最大值为3,f(x)的图象在y轴上的截距为2,其相邻两对称轴间的距离为2,则f(1)+f(2)+f(3)+…+f(100)=____________
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com