
题目列表(包括答案和解析)
2.(2007浙江)设 是函数
是函数 的导函数,将
的导函数,将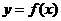 和
和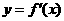 的图象画在同一个直角坐标系中,不可能正确的是(
)
的图象画在同一个直角坐标系中,不可能正确的是(
)
1 选择题
1.设集合 ,
,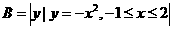 ,则
,则 等于(
)
等于(
)
A. B.
B. C.
C. D.
D.
(二)2008年高考预测
1.在高考题中,数形结合的题目主要出现在函数、导数、解析几何及不等式最值等综合性题目上,把图象作为工具、载体,以此寻求解题思路或制定解题方案,真正体现数形结合的简捷、灵活特点的多是选择、填空等小题。
2.从近三年全国高考卷来看,全国卷与其它省市卷相比,涉及数形结合的题目略少,预测2008年可能有所加强。因为对数形结合等思想方法的考查,是对数学知识在更高层次的抽象和概括能力的考查,是对学生思维品质和数学技能的考查,是考纲明确的一个命题方向。
(一)方法总结
1.数形结合,数形转化常从一下几个方面:
(1)集合的运算及文氏图
(2)函数图象,导数的几何意义
(3)解析几何中方程的曲线
(4)数形转化,以形助数的还有:数轴、函数图象、单位圆、三角函数线或数式的结构特征等;
2.取值范围,最值问题,方程不等式解的讨论,有解与恒成立问题等等,许多问题还可以通过换元转化为具有明显几何意义的问题,借助图形求解。
8.(2006福建)已知函数
(I)求 在区间
在区间 上的最大值
上的最大值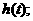
(II)是否存在实数 使得
使得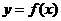 的图象与
的图象与 的图象有且只有三个不同的交点?若存在,求出
的图象有且只有三个不同的交点?若存在,求出 的取值范围;若不存在,说明理由。
的取值范围;若不存在,说明理由。
分析:本题是利用导数方法讨论单调性、最值和方程的解的问题,这些都离不开函数的图象,要通过画图或想着图一步步解答。
解:(I)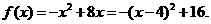
当 时,(如图11)
时,(如图11) 在
在 上单调递减,
上单调递减,

当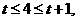 即
即 时,
时,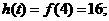
当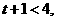 即
即 时,
时, 在
在 上单调递增,
上单调递增,
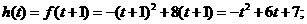
综上,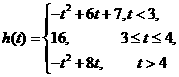
(II)函数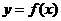 的图象与
的图象与 的图象有且只有三个不同的交点(如图12),即函数
的图象有且只有三个不同的交点(如图12),即函数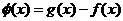 的图象与
的图象与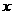 轴的正半轴有且只有三个不同的交点。
轴的正半轴有且只有三个不同的交点。
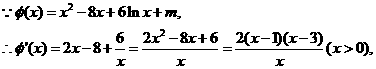
当 时,
时, 是增函数;
是增函数;
当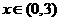 时,
时, 是减函数;
是减函数;
当 时,
时, 是增函数;
是增函数;
当 或
或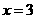 时,
时,
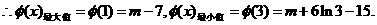
 当
当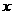 充分接近0时,
充分接近0时, 当
当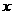 充分大时,
充分大时,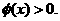
 要使
要使 的图象与
的图象与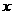 轴正半轴有三个不同的交点,必须且只须
轴正半轴有三个不同的交点,必须且只须
 即
即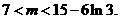
所以存在实数 ,使得函数
,使得函数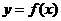 与
与 的图象有且只有三个不同的交点,
的图象有且只有三个不同的交点, 的取值范围为
的取值范围为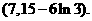
点评:本题主要考查函数的单调性、极值、最值等基本知识,考查运用导数研究函数性质的方法,考查函数与方程、数形结合、分类与整合等数学思想方法和分析问题、解决问题的能力。
7.求函数 的值域。
的值域。
分析:本题需要去绝对值化为分段函数,再按直线x=a相对于两个抛物线的对称轴的位置分类讨论,借助于图象可有效帮助解题。
解:
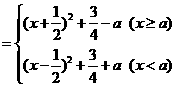
(1)当 时,如图8知
时,如图8知

(2)当 时,如图9
时,如图9
知
(3)当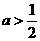 时,如图10
时,如图10
知,
综上所述:当 时,值域为
时,值域为
当 时,值域为
时,值域为
当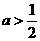 时,值域为
时,值域为
点评:分段去绝对值,数形结合,分类讨论。
6.已知关于x的实系数二次方程x2+ax+b=0有两个实数根α,β.证明:
(Ⅰ)如果│α│<2,│β│<2,那么2│a│<4+b且│b│<4;
(Ⅱ)如果2│a│<4+b且│b│<4,那么│α│<2,│β│<2.
分析:借助函数图像讨论方程的解是很直观有效的方法,由函数y=x2+ax+b的图像(如图7)易知│α│<2,│β│<2,
证明:根据韦达定理│b│=│αβ│<4.
因为二次函数f(x)=x2+ax+b开口向上,│α│<2,│β│<2.
故必有f(±2)>0,即4+2a+b>0, 2a>-(4+b);
4-2a+b>0, 2a<4+b.
∴2│a│<4+b.
(Ⅱ)由 2│a│<4+b 得 4+2a+b>0
即 22+2a+b>0 f(2)>0. ①
及 4-2a+b>0 即 (-2)2+(-2)a+b>0,f(-2)>0. ②
由此可知f(x)=0的每个实根或者在区间(-2,2)之内或者在(-2,2)之外.若两根α,β均落在(-2,2)之外,则与│b│=│αβ│<4矛盾.
若α(或β)落在(-2,2)外,则由于│b│=│αβ│<4,另一个根β(或α)必须落在(-2,2)内,则与①、②式矛盾.
综上所述α,β均落在(-2,2)内.
∴│α│<2,│β│<2.
点评:这是1993年全国高考题的压轴题,标准答案中给的第一解法是利用求根公式写出两根,再由已知求出 的范围,再转化为a、b的关系,有一定的难度。但是利用数形结合,由二次函数的图象讨论实根分布问题,就容易多了,其压轴功能就大打了折扣。
的范围,再转化为a、b的关系,有一定的难度。但是利用数形结合,由二次函数的图象讨论实根分布问题,就容易多了,其压轴功能就大打了折扣。
5.已知xy<0,并且4x -9y
-9y =36.由此能否确定一个函数关系y=f(x)?如果能,求出其解析式、定义域和值域;如果不能,请说明理由.
=36.由此能否确定一个函数关系y=f(x)?如果能,求出其解析式、定义域和值域;如果不能,请说明理由.
分析: 4x -9y
-9y =36在解析几何中表示双曲线的方程,反映了变量x、y之间的对应关系,但还不一定是函数关系,函数中一个x只能对应唯一确定的y,即图像上看不能有“上下重叠”的点。但加上条件xy<0呢?画出图形(如图5)则一目了然。
=36在解析几何中表示双曲线的方程,反映了变量x、y之间的对应关系,但还不一定是函数关系,函数中一个x只能对应唯一确定的y,即图像上看不能有“上下重叠”的点。但加上条件xy<0呢?画出图形(如图5)则一目了然。
解: ,故
,故
解得 ,
,
又

因此能确定一个函数关系y=f(x).其定义域为(-∞,-3)∪)3,+∞).且不难得到其值域为(-∞,0)∪(0,+∞).
点评:本例考查对函数概概念的理解,揭示了函数与解析几何中方程的内在联系--任何一个函数的解析式都可看作一个方程,但方程中x与y的对应关系未必是一个函数.要要处理好这个关系,又如:
(2006全国I.20)在平面直角坐标系 中,有一个以
中,有一个以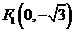 和
和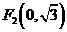 为焦点、离心率为
为焦点、离心率为 的椭圆,设椭圆在第一象限的部分为曲线C,动点P在C上,C在点P处的切线与
的椭圆,设椭圆在第一象限的部分为曲线C,动点P在C上,C在点P处的切线与 轴的交点分别为A、B,且向量
轴的交点分别为A、B,且向量 。求:
。求:
(Ⅰ)点M的轨迹方程; [(Ⅱ) 的最小值]。
的最小值]。
解:(I)……易得椭圆方程的方程为:
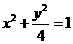 (x>0,y>0)
(x>0,y>0)
下面想要通过导数确定过第一象限点P(x0,y0) (0<x0<1)切线的斜率,就要建立x与y的函数关系,结合图形(如图6)可知:
y=2(0<x<1)
(而不能是 )
)
 又
又 ,
, ,
,
所以切线AB的方程为:
从而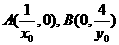 ,又
,又 ,设M(x,y)
,设M(x,y)
由=+可得M的轨迹方程为: + =1 (x>1,y>2)
4. 解三角不等式组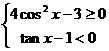
分析:利用三角函数的图像或三角函数线(如图4)求解,先求出一个周期上的解再写出全部。
解答: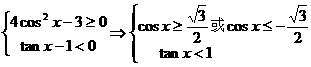
由图得解集为:
点评:三角函数图像和三角函数线,是处理三角函数值大小问题的两个有力武器,用好它会使解题简捷、高效。
3.设集全 ,且
,且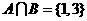 ,求有序集合组{A,B,C}的个数(不同的顺序算不同的组)。
,求有序集合组{A,B,C}的个数(不同的顺序算不同的组)。
解析:借助文氏图(图3)可知,三个集合A、B、C把全集U分成八个部分,需按1、3是否属于C分类,再把2、4、5三个数放到如图中①②③④⑤五个位置即可,每一种放法对应一个有序集合组。
按1、3是否属于C分四类:
(1)1、3 C; (2)1∈C且3
C; (2)1∈C且3 C;
C;
(3)3∈C且1 C; (4)1、3∈C
C; (4)1、3∈C
共有53×4=500种。
点评:画出文氏图,提高了解题的直观性,使解题思路清晰,分类清楚,易于操作。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com