
题目列表(包括答案和解析)
4.分析:解决此题的关键在于由条件式的结构联想到直线方程.进而由A、B两点坐标特点知其在单位圆上.还要根据图形的性质分析清楚结论的几何意义,这样才能巧用数形结合方法完成解题.

证明:在平面直角坐标系中,点A(cosα,sinα)与点B(cosβ,
sinβ)是直线l:ax+by=c与单位圆x2+y2=1的两个交点如图.
从而:|AB|2=(cosα–cosβ)2+(sinα–sinβ)2
=2–2cos(α–β)
又∵单位圆的圆心到直线l的距离
由平面几何知识知|OA|2–( |AB|)2=d2即
|AB|)2=d2即

∴ .
.
3.解:(1)
(2)方程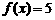 的解分别是
的解分别是 和
和 ,由于
,由于 在
在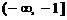 和
和 上单调递减,在
上单调递减,在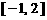 和
和 上单调递增,因此
上单调递增,因此
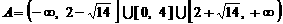 .
.
由于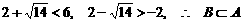 .
.
(3)解法一:当 时,
时, .
.


 ,
,
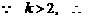
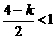 . 又
. 又 ,
,
① 当 ,即
,即 时,取
时,取 ,
,

 .
.
 ,
,
则 .
.
② 当 ,即
,即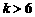 时,取
时,取 ,
,  =
= .
.
由 ①、②可知,当 时,
时,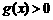 ,
, .
.
因此,在区间 上,
上,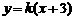 的图像位于函数
的图像位于函数 图像的上方.
图像的上方.
解法二:当 时,
时, .
.
由 得
得 ,
,
令  ,解得
,解得  或
或 ,
,
在区间 上,当
上,当 时,
时,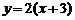 的图像与函数
的图像与函数 的图像只交于一点
的图像只交于一点 ;当
;当 时,
时, 的图像与函数
的图像与函数 的图像没有交点.
的图像没有交点.
如图可知,由于直线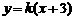 过点
过点 ,当
,当 时,直线
时,直线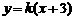 是由直线
是由直线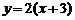 绕点
绕点 逆时针方向旋转得到. 因此,在区间
逆时针方向旋转得到. 因此,在区间 上,
上,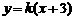 的图像位于函数
的图像位于函数 图像的上方.
图像的上方.
2.解:由定义知1-x2≥0且2+x≠0
∴ -1≤x≤1,故可设x=cosθ,θ∈[0,π],则有 可看作是动点M(cosθ,sinθ)(θ∈[0,π])与定点A(-2,0)连线的斜率,而动点M的轨迹方程
可看作是动点M(cosθ,sinθ)(θ∈[0,π])与定点A(-2,0)连线的斜率,而动点M的轨迹方程 ,θ∈[0,π],即x2+y2=1(y∈[0,1]是半圆。
,θ∈[0,π],即x2+y2=1(y∈[0,1]是半圆。
设切线为AT,T为切点,|OT|=1,|OA|=2
∴ 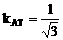 ,∴0≤kAM≤
,∴0≤kAM≤
即函数的值域为[0, ],故最大值为
],故最大值为 。
。

1.解:原不等式化为(x2-1)m-(2x-1)<0记f(m)=(x2-1)m-(2x-1)
(-2≤m≤2),其图像是线段。结合图像和题意知,只须:
f(-2)=-2(x2-1)-(2x-1)<0
f(2)=2(x2-1)-(2x-1)<0
即 2x2+2x-3>0
2x2-2x-1<0
解之,x的取值范围为
4.解析:由已知画出y=f(x)的图象可知:
当x∈(-1,0)∪(1,+∞)时f(x)>0
当x∈(-∞,-1)∪(0,1)时 f(x)<0
又x(x- )=(x-
)=(x-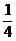 )2-
)2- ≥-
≥- >-1
>-1
∴f(x(x- ))<0成立,则必有
))<0成立,则必有
0<x(x- )<1,解之得:
)<1,解之得: <x<0或
<x<0或 <x<
<x<
解答题
3.设u=x2-1,化原式为: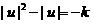 ,
,
画出函数 的图象,看使u≥-1的解的个数,可知假命题的个数为0。
的图象,看使u≥-1的解的个数,可知假命题的个数为0。
2.解析:由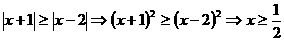 ,
,
 如右图
如右图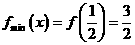
1.画出 的图象可知,有四个交点则
的图象可知,有四个交点则 ;
;
2. 设函数 =
= x2+8x+3 (
x2+8x+3 ( <0),对于给定的负数
<0),对于给定的负数 ,有一个最大的正数
,有一个最大的正数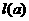 ,使得在整个区间[0,
,使得在整个区间[0,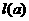 ]上,不等式|
]上,不等式| |≤5都成立。问
|≤5都成立。问 为何值时
为何值时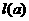 最大?求出这个最大的
最大?求出这个最大的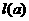 ,证明你的结论。
,证明你的结论。
解析答案:
选择题:1-12:ADCCB CBAAD BB
填空题:
1. 
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com