
题目列表(包括答案和解析)
3.利用向量的坐标运算,用已知向量表示未知向量
[例4]
已知点 是
是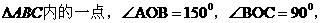
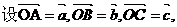 且
且 试用
试用
解:以O为原点,OC,OB所在的直线为 轴和
轴和 轴建立如图3所示的坐标系.
轴建立如图3所示的坐标系.
由OA=2,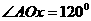 ,所以
,所以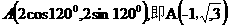 ,
,
 易求
易求 ,设
,设

 .
.
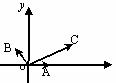
[例5] 如图,

用 表示
表示
解:以O为坐标原点,以OA所在的直线为 轴,建立如图所示的直角坐标系,则
轴,建立如图所示的直角坐标系,则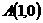 ,
,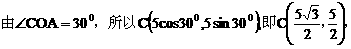


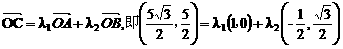
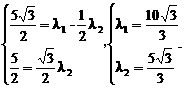
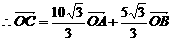 .
.
2.利用向量的坐标运算,解决有关线段的长度问题
[例3]
已知 ,AD为中线,求证
,AD为中线,求证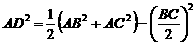
证明:以B为坐标原点,以BC所在的直线为 轴建立如图2直角坐标系,
轴建立如图2直角坐标系,
 设
设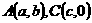 ,
, ,
,
则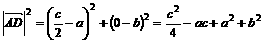 ,
,
 .
.
= ,
,
从而
 ,
,
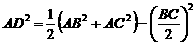 .
.
平面向量
[例1] 在下列各命题中为真命题的是( )
①若 =(x1,y1)、
=(x1,y1)、 =(x2,y2),则
=(x2,y2),则 ·
· =x1y1+x2y2
=x1y1+x2y2
②若A(x1,y1)、B(x2,y2),则| |=
|=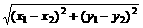
③若 =(x1,y1)、
=(x1,y1)、 =(x2,y2),则
=(x2,y2),则 ·
· =0
=0 x1x2+y1y2=0
x1x2+y1y2=0
④若 =(x1,y1)、
=(x1,y1)、 =(x2,y2),则
=(x2,y2),则 ⊥
⊥
 x1x2+y1y2=0
x1x2+y1y2=0
A、①② B、②③ C、③④ D、①④
解:根据向量数量积的坐标表示;若 =(x1,y1),
=(x1,y1),  =(x2,y2),则
=(x2,y2),则 ·
· =x1x2+y1y2,对照命题(1)的结论可知,它是一个假命题、
=x1x2+y1y2,对照命题(1)的结论可知,它是一个假命题、
于是对照选择支的结论、可以排除(A)与(D),而在(B)与(C)中均含有(3)、故不必对(3)进行判定,它一定是正确的、对命题(2)而言,它就是两点间距离公式,故它是真命题,这样就以排除了(C),应选择(B)、
说明:对于命题(3)而言,由于 ·
· =0
=0
 =
=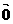 或
或 =
=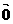 或
或 ⊥
⊥
 x1x2+y1y2=0,故它是一个真命题、
x1x2+y1y2=0,故它是一个真命题、
而对于命题(4)来讲, ⊥
⊥
 x1x2+y1y2=0、但反过来,当x1x2+y1y2=0时,可以是x1=y1=0,即
x1x2+y1y2=0、但反过来,当x1x2+y1y2=0时,可以是x1=y1=0,即 =
=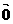 ,而我们的教科书并没有对零向量是否与其它向量垂直作出规定,因此x1x2+y1y2=0
,而我们的教科书并没有对零向量是否与其它向量垂直作出规定,因此x1x2+y1y2=0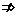
 ⊥
⊥ ),所以命题(4)是个假命题、
),所以命题(4)是个假命题、
[例2]
已知 =(-
=(-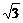 ,-1),
,-1),  =(1,
=(1, 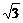 ),那么
),那么 ,
, 的夹角θ=( )
的夹角θ=( )
A、30° B、60° C、120° D、150°
解: ·
· =(-
=(-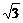 ,-1)·(1,
,-1)·(1,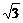 )=-2
)=-2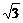
| |=
|= =2
=2
| |=
|= =2
=2
∴cosθ=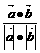 =
= =
=
[例3]
已知 =(2,1),
=(2,1),  =(-1,3),若存在向量
=(-1,3),若存在向量 使得:
使得: ·
· =4,
=4,  ·
· =-9,试求向量
=-9,试求向量 的坐标、
的坐标、
解:设 =(x,y),则由
=(x,y),则由 ·
· =4可得:
=4可得:
2x+y=4;又由 ·
· =-9可得:-x+3y=-9
=-9可得:-x+3y=-9
于是有: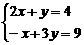
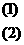
由(1)+2(2)得7y=-14,∴y=-2,将它代入(1)可得:x=3
∴ =(3,-2)、
=(3,-2)、
说明:已知两向量 ,
, 可以求出它们的数量积
可以求出它们的数量积 ·
· ,但是反过来,若已知向量
,但是反过来,若已知向量 及数量积
及数量积 ·
· ,却不能确定
,却不能确定 、
、
[例4]
求向量 =(1,2)在向量
=(1,2)在向量 =(2,-2)方向上的投影、
=(2,-2)方向上的投影、
解:设向量 与
与 的夹角θ、
的夹角θ、
有cosθ=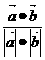 =
= =-
=-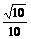
∴ 在
在 方向上的投影=|
方向上的投影=| |cosθ=
|cosθ= ×(-
×(-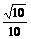 )=-
)=-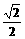
[例5]
已知△ABC的顶点分别为A(2,1),B(3,2),C(-3,-1),BC边上的高AD,求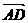 及点D的坐标、
及点D的坐标、
解:设点D的坐标为(x,y)
∵AD是边BC上的高,
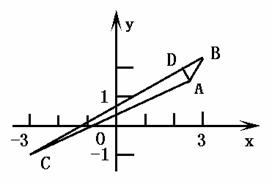 ∴AD⊥BC,∴
∴AD⊥BC,∴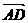 ⊥
⊥
又∵C、B、D三点共线,
∴ ∥
∥
又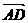 =(x-2,y-1),
=(x-2,y-1),
 =(-6,-3)
=(-6,-3)
 =(x-3,y-2)
=(x-3,y-2)
∴
解方程组,得x= ,y=
,y=
∴点D的坐标为( ,
, ),
),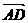 的坐标为(-
的坐标为(-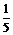 ,
, )
)
[例6]
设向量 、
、 满足:|
满足:| |=|
|=| |=1,且
|=1,且 +
+ =(1,0),求
=(1,0),求 ,
, 、
、
解:∵| |=|
|=| |=1,
|=1,
∴可设 =(cosα,sinα),
=(cosα,sinα),
 =(cosβ,sinβ)、
=(cosβ,sinβ)、
∵ +
+ =(cosα+cosβ,sinα+sinβ)=(1,0),
=(cosα+cosβ,sinα+sinβ)=(1,0),
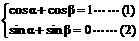
由(1)得:cosα=1-cosβ……(3)
由(2)得:sinα=-sinβ……(4)
∴cosα=1-cosβ=
∴sinα=± ,sinβ=
,sinβ=

 或
或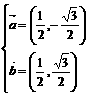
[例7]
对于向量的集合A={ =(x,y)|x2+y2≤1}中的任意两个向量
=(x,y)|x2+y2≤1}中的任意两个向量 、
、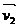 与两个非负实数α、β;求证:向量α
与两个非负实数α、β;求证:向量α +β
+β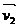 的大小不超过α+β、
的大小不超过α+β、
证明:设 =(x1,y1),
=(x1,y1),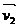 =(x2,y2)
=(x2,y2)
根据已知条件有:x21+y21≤1,x22+y22≤1
又因为|α +β
+β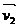 |=
|=
=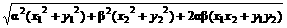
其中x1x2+y1y2≤
 ≤1
≤1
所以|α +β
+β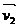 |≤
|≤ =|α+β|=α+β
=|α+β|=α+β
[例8]
已知梯形ABCD中,AB∥CD,∠CDA=∠DAB=90°,CD=DA= AB、
AB、
求证:AC⊥BC
证明:以A为原点,AB所在直线为x轴,建立直角坐标系、如图,设AD=1
 则A(0,0)、B(2,0)、C(1,1)、D(0,1)
则A(0,0)、B(2,0)、C(1,1)、D(0,1)
∴ =(-1,1),
=(-1,1),  =(1,1)
=(1,1)
 ·
· =-1×1+1×1=0
=-1×1+1×1=0
∴BC⊥AC、
[例9] 已知A(0,a),B(0,b),(0<a<b),在x轴的正半轴上求点C,使∠ACB最大,并求出最大值、
解,设C(x,0)(x>0)
则 =(-x,a),
=(-x,a), 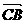 =(-x,b)
=(-x,b)
则 ·
·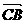 =x2+ab、
=x2+ab、
cos∠ACB= =
=
令t=x2+ab
故cos∠ACB=
当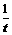 =
= 即t=2ab时,cos∠ACB最大值为
即t=2ab时,cos∠ACB最大值为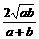 、
、
当C的坐标为( ,0)时,∠ACB最大值为arccos
,0)时,∠ACB最大值为arccos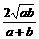 、
、
[例10]
 如图,四边形ABCD是正方形,P是对角线BD上的一点,PECF是矩形,用向量法证明
如图,四边形ABCD是正方形,P是对角线BD上的一点,PECF是矩形,用向量法证明
(1)PA=EF (2)PA⊥EF
证明:建立如图所示坐标系,设正方形边长为1,
| |=λ,则A(0,1),P(
|=λ,则A(0,1),P(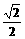 λ,
λ,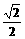 λ),E(1,
λ),E(1,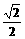 λ),F(
λ),F(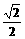 λ,0)
λ,0)
∴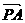 =(-
=(-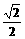 λ,1-
λ,1-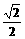 λ),
λ), 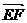 =(
=(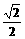 λ-1,-
λ-1,- 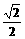 λ)
λ)
(1)|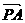 |2=(-
|2=(-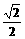 λ)2+(1-
λ)2+(1-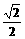 λ)2=λ2-
λ)2=λ2- λ+1
λ+1
|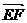 |2=(
|2=(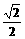 λ-1)2+(-
λ-1)2+(-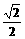 λ)2=λ2-
λ)2=λ2- λ+1
λ+1
∴|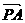 |2=|
|2=|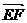 |2,故PA=EF
|2,故PA=EF
(2) 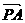 ·
·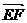 =(-
=(-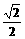 λ)(
λ)(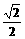 λ-1)+(1-
λ-1)+(1-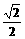 λ)(-
λ)(-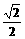 λ)=0
λ)=0
∴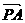 ⊥
⊥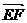 ∴PA⊥EF、
∴PA⊥EF、
[例11]
已知
① 求 ;
;
②当k为何实数时,k
 与
与 平行, 平行时它们是同向还是反向?
平行, 平行时它们是同向还是反向?
解:① = (1,0) + 3(2,1) = ( 7,3) , ∴
= (1,0) + 3(2,1) = ( 7,3) , ∴ =
=  =
=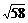 .
.
②k
 = k(1,0)-(2,1)=(k-2,-1).
= k(1,0)-(2,1)=(k-2,-1).
设k
 =λ(
=λ( ),即(k-2,-1)=
λ(7,3),
),即(k-2,-1)=
λ(7,3),
∴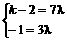
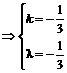 .
.
故k=  时, 它们反向平行.
时, 它们反向平行.
[例12]
已知
 与
与 的夹角为
的夹角为 ,若向量
,若向量 与
与 垂直, 求k.
垂直, 求k.
解: =2×1×
=2×1× =1.
=1.
∵ 与
与 垂直,
垂直,
∴( )
) =
= 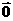 ,
,
∴2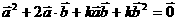
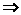 k = - 5.
k = - 5.
[例13] 如果△ABC的三边a、b、c满足b2 + c 2 = 5a2,BE、CF分别为AC边与AB上的中线, 求证:BE⊥CF.
解:
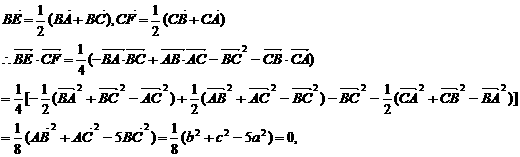
∴ ⊥
⊥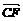 , 即 BE⊥CF .
, 即 BE⊥CF .
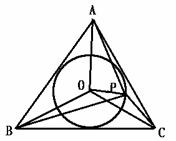
[例14] 是否存在4个平面向量,两两不共线,其中任何两个向量之和均与其余两个向量之和垂直?
解:如图所示,在正△ABC中,O为其内心,P为圆周上一点,
满足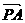 ,
, ,
,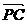 ,
, 两两不共线,有
两两不共线,有
(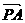 +
+ )·(
)·(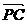 +
+ )
)
=( +
+ +
+ +
+ )·(
)·( +
+ +
+ )
)
 =(2
=(2 +
+ +
+ )·(2
)·(2 +
+ )
)
=(2 -
- )·(2
)·(2 +
+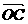 )
)
=4 2-
2-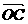 2
2
=4 2-
2-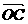 2=0
2=0
有(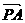 +
+ )与(
)与(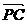 +
+ )垂直、
)垂直、
同理证其他情况、从而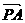 ,
, ,
,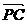 ,
, 满足题意、故存在这样4个平面向量、
满足题意、故存在这样4个平面向量、
平面向量的综合应用
1.利用向量的坐标运算,解决两直线的夹角,判定两直线平行、垂直问题
[例1]
已知向量 满足条件
满足条件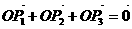 ,
, ,求证:
,求证: 是正三角形
是正三角形
解:令O为坐标原点,可设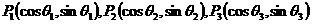
由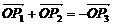 ,即
,即
|
|

两式平方和为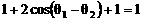 ,
, ,
,
由此可知 的最小正角为
的最小正角为 ,即
,即 与
与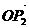 的夹角为
的夹角为 ,
,
同理可得 与
与 的夹角为
的夹角为 ,
, 与
与 的夹角为
的夹角为 ,
,
这说明 三点均匀分部在一个单位圆上,
三点均匀分部在一个单位圆上,
所以 为等腰三角形.
为等腰三角形.
[例2] 求等腰直角三角形中两直角边上的中线所成的钝角的度数
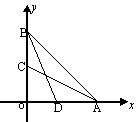 解:如图,分别以等腰直角三角形的两直角边为
解:如图,分别以等腰直角三角形的两直角边为 轴、
轴、
轴建立直角坐标系,设 ,则
,则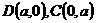 ,
,
从而可求: ,
,
 =
= .
.
 .
.
由于本章知识分向量与解斜三角形两部分,所以应用本章知识解决的问题也分为两类:一类是根据向量的概念、定理、法则、公式对向量进行运算,并能运用向量知识解决平面几何中的一些计算和证明问题;另一类是运用正、余弦定理正确地解斜三角形,并能应用解斜三角形知识解决测量不可到达的两点间的距离问题。
在解决关于向量问题时,一是要善于运用向量的平移、伸缩、合成、分解等变换,正确地进行向量的各种运算,进一步加深对“向量”这一二维性的量的本质的认识,并体会用向量处理问题的优越性。二是向量的坐标运算体现了数与形互相转化和密切结合的思想,所以要通过向量法和坐标法的运用,进一步体会数形结合思想在解决数学问题上的作用。
在解决解斜三角形问题时,一方面要体会向量方法在解三角形方面的应用,另一方面要体会解斜三角形是重要的测量手段,通过学习提高解决实际问题的能力。
3.向量在空间中的应用(在B类教材中).在空间坐标系下,通过向量的坐标的表示,运用计算的方法研究三维空间几何图形的性质.
在复习过程中,抓住源于课本,高于课本的指导方针.本章考题大多数是课本的变式题,即源于课本.因此,掌握双基、精通课本是本章关键.分析近几年来的高考试题,有关平面向量部分突出考查了向量的基本运算。对于和解析几何相关的线段的定比分点和平移等交叉内容,作为学习解析几何的基本工具,在相关内容中会进行考查。本章的另一部分是解斜三角形,它是考查的重点。总而言之,平面向量这一章的学习应立足基础,强化运算,重视应用。考查的重点是基础知识和基本技能。
2.以解答题考查圆锥曲线中的典型问题.此类题综合性比较强,难度大,以解析几何中的常规题为主.
对本章内容的考查主要分以下三类:
1.以选择、填空题型考查本章的基本概念和性质.此类题一般难度不大,用以解决有关长度、夹角、垂直、判断多边形形状等问题.
1、理解向量的概念,掌握向量的几何表示,了解共线向量的概念。2、掌握向量的加法和减法的运算法则及运算律。3、掌握实数与向量的积的运算法则及运算律,理解两个向量共线的充要条件。4、了解平面向量基本定理,理解平面向量的坐标的概念,掌握平面向量的坐标运算。5、掌握平面向量的数量积及其几何意义,了解用平面向量的数量积可以处理有关长度、角度和垂直的问题,掌握向量垂直的条件。6、掌握线段的定比分点和中点坐标公式,并且能熟练运用;掌握平移公式。7、掌握正、余弦定理,并能初步运用它们解斜三角形。8、通过解三角形的应用的教学,继续提高运用所学知识解决实际问题的能力。
8.(★★★★★)设实数q满足|q|<1,数列{an}满足:a1=2,a2≠0,an·an+1=-qn,求an表达式,又如果 S2n<3,求q的取值范围.
S2n<3,求q的取值范围.
7.(★★★★★)已知数列{bn}是等差数列,b1=1,b1+b2+…+b10=145.
(1)求数列{bn}的通项公式bn;
(2)设数列{an}的通项an=loga(1+ )(其中a>0且a≠1)记Sn是数列{an}的前n项和,试比较Sn与
)(其中a>0且a≠1)记Sn是数列{an}的前n项和,试比较Sn与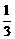 logabn+1的大小,并证明你的结论.
logabn+1的大小,并证明你的结论.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com