
题目列表(包括答案和解析)
2.中心在原点,焦点在坐标为(0,±5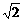 )的椭圆被直线3x-y-2=0截得的弦的中点的横坐标为
)的椭圆被直线3x-y-2=0截得的弦的中点的横坐标为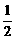 ,则椭圆方程为( )
,则椭圆方程为( )

1.已知直线x+2y-3=0与圆x2+y2+x-6y+m=0相交于P、Q两点,O为坐标原点,若OP⊥OQ,则m等于( )
A.3 B.-3 C.1 D.-1
高考圆锥曲线试题一般有3题(1个选择题, 1个填空题, 1个解答题), 共计22分左右, 考查的知识点约为20个左右. 其命题一般紧扣课本, 突出重点, 全面考查. 选择题和填空题考查以圆锥曲线的基本概念和性质为主, 难度在中等以下,一般较容易得分,解答题常作为数学高考中的压轴题,综合考查学生数形结合、等价转换、分类讨论、逻辑推理等诸方面的能力,重点考查圆锥曲线中的重要知识点, 通过知识的重组与链接, 使知识形成网络, 着重考查直线与圆锥曲线的位置关系, 往往结合平面向量进行求解,在复习应充分重视。
求圆锥曲线的方程
[复习要点]
求指定的圆锥曲线的方程是高考命题的重点,主要考查识图、画图、数形结合、等价转化、分类讨论、逻辑推理、合理运算及创新思维能力,解决好这类问题,除要求熟练掌握好圆锥曲线的定义、性质外,命题人还常常将它与对称问题、弦长问题、最值问题等综合在一起命制难度较大的题,解决这类问题常用定义法和待定系数法.
一般求已知曲线类型的曲线方程问题,可采用“先定形,后定式,再定量”的步骤.
定形--指的是二次曲线的焦点位置与对称轴的位置.
定式--根据“形”设方程的形式,注意曲线系方程的应用,如当椭圆的焦点不确定在哪个坐标轴上时,可设方程为mx2+ny2=1(m>0,n>0).
定量--由题设中的条件找到“式”中特定系数的等量关系,通过解方程得到量的大小.
[例题]
[例1]
双曲线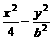 =1(b∈N)的两个焦点F1、F2,P为双曲线上一点,
=1(b∈N)的两个焦点F1、F2,P为双曲线上一点,
|OP|<5,|PF1|,|F1F2|,|PF2|成等比数列,则b2=_________.
解:设F1(-c,0)、F2(c,0)、P(x,y),则
|PF1|2+|PF2|2=2(|PO|2+|F1O|2)<2(52+c2),
即|PF1|2+|PF2|2<50+2c2,
又∵|PF1|2+|PF2|2=(|PF1|-|PF2|)2+2|PF1|·|PF2|,
依双曲线定义,有|PF1|-|PF2|=4,
依已知条件有|PF1|·|PF2|=|F1F2|2=4c2
∴16+8c2<50+2c2,∴c2<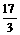 ,
,
又∵c2=4+b2<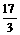 ,∴b2<
,∴b2<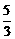 ,∴b2=1.
,∴b2=1.
答案:1
[例2]
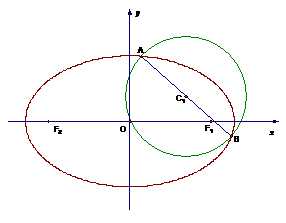
已知圆C1的方程为 ,椭圆C2的方程为
,椭圆C2的方程为
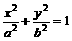
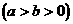 ,C2的离心率为
,C2的离心率为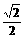 ,如果C1与C2相交于A、B两点,且线段AB恰为圆C1的直径,求直线AB的方程和椭圆C2的方程。
,如果C1与C2相交于A、B两点,且线段AB恰为圆C1的直径,求直线AB的方程和椭圆C2的方程。
解:由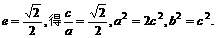
设椭圆方程为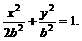
设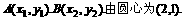

又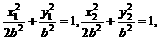
两式相减,得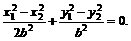
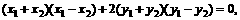
又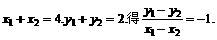
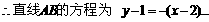
即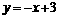
将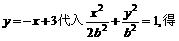
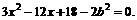

由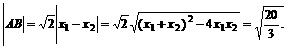
得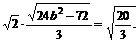
解得 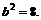 故所有椭圆方程
故所有椭圆方程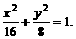
[例3]
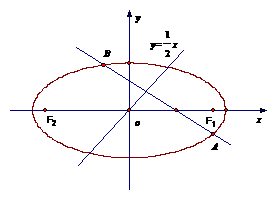
过点(1,0)的直线l与中心在原点,焦点在x轴上且离心率为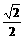 的椭圆C相交于A、B两点,直线y=
的椭圆C相交于A、B两点,直线y=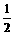 x过线段AB的中点,同时椭圆C上存在一点与右焦点关于直线l对称,试求直线l与椭圆C的方程.
x过线段AB的中点,同时椭圆C上存在一点与右焦点关于直线l对称,试求直线l与椭圆C的方程.
解法一:由e=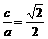 ,得
,得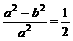 ,从而a2=2b2,c=b.
,从而a2=2b2,c=b.
设椭圆方程为x2+2y2=2b2,A(x1,y1),B(x2,y2)在椭圆上.
则x12+2y12=2b2,x22+2y22=2b2,两式相减得,
(x12-x22)+2(y12-y22)=0,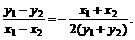
 设AB中点为(x0,y0),则kAB=-
设AB中点为(x0,y0),则kAB=-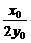 ,
,
又(x0,y0)在直线y=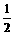 x上,y0=
x上,y0=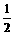 x0,
x0,
于是-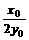 =-1,kAB=-1,
=-1,kAB=-1,
设l的方程为y=-x+1.
右焦点(b,0)关于l的对称点设为(x′,y′),
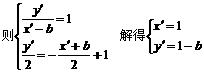
由点(1,1-b)在椭圆上,得1+2(1-b)2=2b2,b2=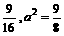 .
.
∴所求椭圆C的方程为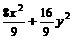 =1,l的方程为y=-x+1.
=1,l的方程为y=-x+1.
解法二:由e=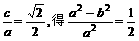 ,从而a2=2b2,c=b.
,从而a2=2b2,c=b.
设椭圆C的方程为x2+2y2=2b2,l的方程为y=k(x-1),
将l的方程代入C的方程,得(1+2k2)x2-4k2x+2k2-2b2=0,
则x1+x2=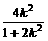 ,y1+y2=k(x1-1)+k(x2-1)=k(x1+x2)-2k=-
,y1+y2=k(x1-1)+k(x2-1)=k(x1+x2)-2k=-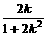 .
.
直线l:y=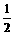 x过AB的中点(
x过AB的中点(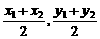 ),则
),则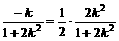 ,
,
解得k=0,或k=-1.
若k=0,则l的方程为y=0,焦点F(c,0)关于直线l的对称点就是F点本身,不能在椭圆C上,所以k=0舍去,从而k=-1,直线l的方程为y=-(x-1),即y=-x+1,以下同解法一.
解法3:设椭圆方程为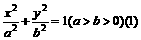
直线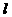 不平行于y轴,否则AB中点在x轴上与直线
不平行于y轴,否则AB中点在x轴上与直线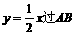 中点矛盾。
中点矛盾。
故可设直线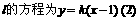

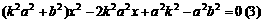
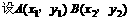 ,
,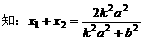
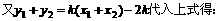
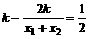 ,
,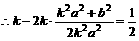 ,
,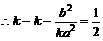 ,
,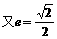
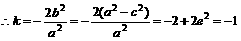 ,
,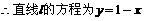 ,
,
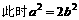 ,
,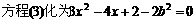 ,
,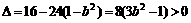
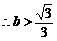 ,
,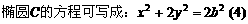 ,
,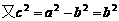 ,
,
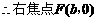 ,
,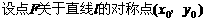 ,
,
则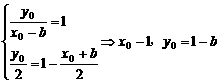 ,
,

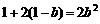 ,
,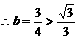 ,
,
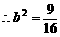 ,
, 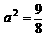
所以所求的椭圆方程为: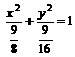
[例4]
如图,已知△P1OP2的面积为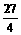 ,P为线段P1P2的一个三等分点,求以直线OP1、OP2为渐近线且过点P的离心率为
,P为线段P1P2的一个三等分点,求以直线OP1、OP2为渐近线且过点P的离心率为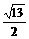 的双曲线方程.
的双曲线方程.
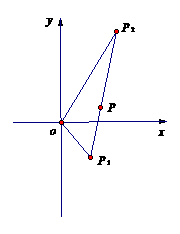 解:以O为原点,∠P1OP2的角平分线为x轴建立如图所示的直角坐标系.
解:以O为原点,∠P1OP2的角平分线为x轴建立如图所示的直角坐标系.
设双曲线方程为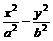 =1(a>0,b>0)
=1(a>0,b>0)
由e2=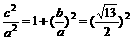 ,得
,得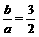 .
.
∴两渐近线OP1、OP2方程分别为y=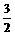 x和y=-
x和y=-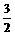 x
x
设点P1(x1, 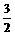 x1),P2(x2,-
x1),P2(x2,-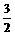 x2)(x1>0,x2>0),
x2)(x1>0,x2>0),
则由点P分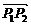 所成的比λ=
所成的比λ= =2,
=2,
得P点坐标为(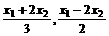 ),
),
又点P在双曲线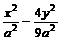 =1上,
=1上,
所以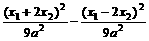 =1,
=1,
即(x1+2x2)2-(x1-2x2)2=9a2,整理得8x1x2=9a2 ①
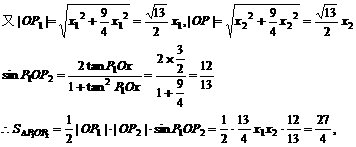
即x1x2= 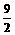 ②
②
由①、②得a2=4,b2=9
故双曲线方程为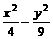 =1.
=1.
[例5]
过椭圆C: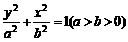 上一动点P引圆O:x2 +y2 =b2的两条切线PA、PB,A、B为切点,直线AB与x轴,y轴分别交于M、N两点。(1) 已知P点坐标为(x0,y0 )并且x0y0≠0,试求直线AB方程;(2) 若椭圆的短轴长为8,并且
上一动点P引圆O:x2 +y2 =b2的两条切线PA、PB,A、B为切点,直线AB与x轴,y轴分别交于M、N两点。(1) 已知P点坐标为(x0,y0 )并且x0y0≠0,试求直线AB方程;(2) 若椭圆的短轴长为8,并且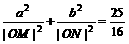 ,求椭圆C的方程;(3) 椭圆C上是否存在点P,由P向圆O所引两条切线互相垂直?若存在,
,求椭圆C的方程;(3) 椭圆C上是否存在点P,由P向圆O所引两条切线互相垂直?若存在, 请求出存在的条件;若不存在,请说明理由。
请求出存在的条件;若不存在,请说明理由。
解:(1)设A(x1,y1),B(x2, y2)
切线PA: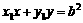 ,PB:
,PB: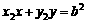
∵P点在切线PA、PB上,∴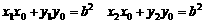
∴直线AB的方程为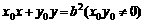
(2)在直线AB方程中,令y=0,则M(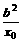 ,0);令x=0,则N(0,
,0);令x=0,则N(0,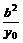 )
)
∴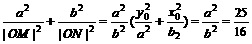 ①
①
∵2b=8 ∴b=4 代入①得a2 =25, b2 =16
∴椭圆C方程: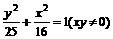 (注:不剔除xy≠0,可不扣分)
(注:不剔除xy≠0,可不扣分)
(3) 假设存在点P(x0,y0)满足PA⊥PB,连接OA、OB由|PA|=|PB|知,
四边形PAOB为正方形,|OP|=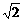 |OA| ∴
|OA| ∴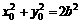 ①
①
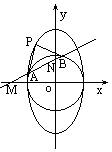
又∵P点在椭圆C上 ∴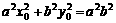 ②
②
由①②知x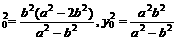
∵a>b>0 ∴a2 -b2>0
(1)当a2-2b2>0,即a>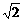 b时,椭圆C上存在点,由P点向圆所引两切线互相垂直;
b时,椭圆C上存在点,由P点向圆所引两切线互相垂直;
(2)当a2-2b2<0,即b<a<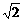 b时,椭圆C上不存在满足条件的P点
b时,椭圆C上不存在满足条件的P点
[例6]
已知椭圆C的焦点是F1(-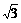 ,0)、F2(
,0)、F2(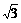 ,0),点F1到相应的准线的距离为
,0),点F1到相应的准线的距离为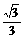 ,过F2点且倾斜角为锐角的直线l与椭圆C交于A、B两点,使得|F2B|=3|F2A|.
,过F2点且倾斜角为锐角的直线l与椭圆C交于A、B两点,使得|F2B|=3|F2A|.
(1)求椭圆C的方程;(2)求直线l的方程.
解:(1)依题意,椭圆中心为O(0,0),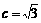
点F1到相应准线的距离为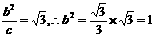 ,
,
 a2=b2+c2=1+3=4
a2=b2+c2=1+3=4
∴所求椭圆方程为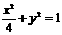
(2)设椭圆的右准线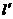 与l交于点P,作AM⊥
与l交于点P,作AM⊥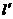 ,AN⊥
,AN⊥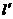 ,垂足
,垂足
分别为M、N. 由椭圆第二定义,
得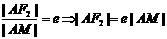
同理|BF2|=e|BN|
由Rt△PAM-Rt△PBN,得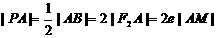 …9分
…9分
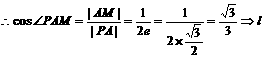 的斜率
的斜率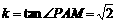 .
.
∴直线l的方程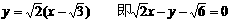
[例7]
已知点B(-1,0),C(1,0),P是平面上一动点,且满足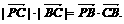
(1)求点P的轨迹C对应的方程;
(2)已知点A(m,2)在曲线C上,过点A作曲线C的两条弦AD和AE,且AD⊥AE,判断:直线DE是否过定点?试证明你的结论.
(3)已知点A(m,2)在曲线C上,过点A作曲线C的两条弦AD,AE,且AD,AE的斜率k1、k2满足k1·k2=2.求证:直线DE过定点,并求出这个定点.
解:(1)设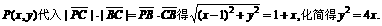
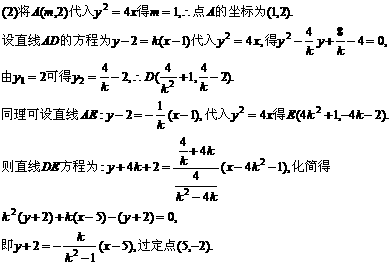

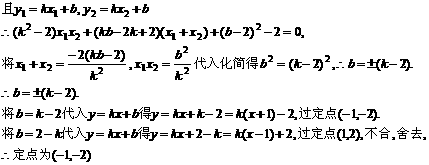
[例8]
已知曲线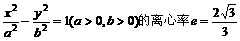 ,直线l过A(a,0)、
,直线l过A(a,0)、
B(0,-b)两点,原点O到l的距离是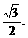
(Ⅰ)求双曲线的方程;
(Ⅱ)过点B作直线m交双曲线于M、N两点,若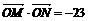 ,求直线m的方程.
,求直线m的方程.
解:(Ⅰ)依题意, 由原点O到l的距离
由原点O到l的距离
为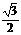 ,得
,得 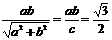 又
又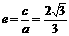
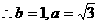
故所求双曲线方程为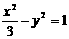
(Ⅱ)显然直线m不与x轴垂直,设m方程为y=kx-1,则点M、N坐标(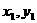 )、
)、
(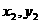 )是方程组
)是方程组 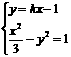 的解
的解
消去y,得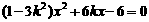 ①
①
依设,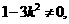 由根与系数关系,知
由根与系数关系,知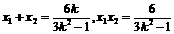
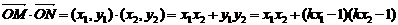
=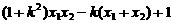 =
=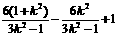
=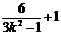
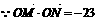 ∴
∴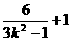 =-23,k=±
=-23,k=±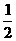
当k=±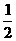 时,方程①有两个不等的实数根
时,方程①有两个不等的实数根
故直线l方程为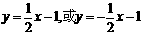
[例9]
已知动点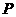 与双曲线
与双曲线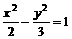 的两个焦点
的两个焦点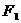 、
、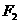 的距离之和为定值,且
的距离之和为定值,且
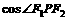 的最小值为
的最小值为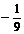 .
.
(1)求动点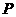 的轨迹方程;
的轨迹方程;
(2)若已知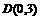 ,
,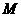 、
、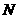 在动点
在动点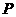 的轨迹上且
的轨迹上且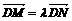 ,求实数
,求实数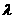 的取值范围.
的取值范围.
解:(1)由已知可得:
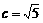 ,
,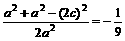
∴ 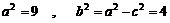
∴ 所求的椭圆方程为 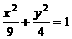 .
.
(2)方法一:
由题知点D、M、N共线,设为直线m,当直线m的斜率存在时,设为k,则直线m的方程为 y = k x +3 代入前面的椭圆方程得
(4+9k 2) x 2 +54 k +45 = 0 ①
由判别式 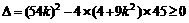 ,得
,得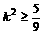 .
.
再设M (x 1 , y 1 ), N ( x 2 , y 2),则一方面有
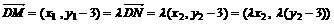 ,得
,得
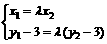
另一方面有 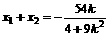 ,
,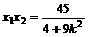 ②
②
将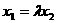 代入②式并消去 x 2可得
代入②式并消去 x 2可得
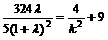 ,由前面知,
,由前面知,
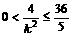
∴ 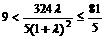 ,解得
,解得 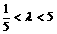 .
.
又当直线m的斜率不存在时,不难验证: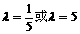 ,
,
所以 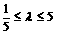 为所求。
为所求。
方法二:同上得
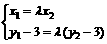
设点M (3cosα,2sinα),N (3cosβ,2sinβ)
则有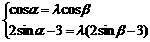
由上式消去α并整理得
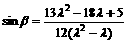 , 由于
, 由于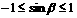
∴ 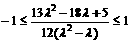 , 解得
, 解得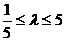 为所求.
为所求.
方法三:设法求出椭圆上的点到点D的距离的最大值为5,最小值为1.
进而推得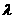 的取值范围为
的取值范围为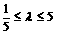 。
。
[求圆锥曲线的方程练习]
考试内容:
. 椭圆及其标准方程.椭圆的简单几何性质.椭圆的参数方程;
. 双曲线及其标准方程.双曲线的简单几何性质;
. 抛物线及其标准方程.抛物线的简单几何性质;
考试要求:
. (1)掌握椭圆的定义、标准方程和椭圆的简单几何性质,理解椭圆的参数方程;
. (2)掌握双曲线的定义、标准方程和双曲线的简单几何性质;
. (3)掌握抛物线的定义、标准方程和抛物线的简单几何性质;
. (4)了解圆锥曲线的初步应用。
(一)曲线和方程,由已知条件列出曲线的方程,曲线的交点
说明 在求曲线方程之前必须建立坐标系,然后根据条件列出等式进行化简 .特别是在求出方程后要考虑化简的过程是否是同解变形,是否满足已知条件,只有这样求 出的曲线方程才能准确无误.另外,要求会判断 曲线间有无交点,会求曲线的交点坐标.
5.坐标变换
坐标变换 在解析几何中,把坐标系的变换(如改变坐标系原点的位置或坐标轴的方向)叫做 坐标变换.实施坐标变换时,点的位置,曲线的形状、大小、位置都不改变,仅仅只改变点 的坐标与曲线的方程.
坐标轴的平移 坐标轴的方向和长度单位不改变,只改变原点的位置,这种坐标系的变换叫 做坐标轴的平移,简称移轴.
坐标轴的平移公式 设平面内任意一点M,它在原坐标系xOy中的坐标是9x,y),在新坐标系x ′O′y′中的坐标是(x′,y′).设新坐标系的原点O′在原坐标系xOy中的坐标是(h,k),则
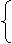
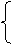 x=x′+h
x′=x-h
x=x′+h
x′=x-h
(1) 或(2)
y=y′+k y′=y-k
公式(1)或(2)叫做平移(或移轴)公式.
中心或顶点在(h,k)的圆锥曲线方程
中心或顶点在(h,k)的圆锥曲线方程见下表.
|
方 程 |
焦 点 |
焦 线 |
对称轴 |
|
|
椭圆 |
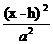 + +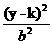 =1 =1 |
(±c+h,k) |
x=±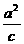 +h +h |
x=h y=k |
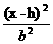 + +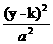 =1 =1 |
(h,±c+k) |
y=±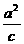 +k +k |
x=h y=k |
|
|
双曲线 |
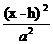 - -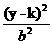 =1 =1 |
(±c+h,k) |
=±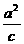 +k +k |
x=h y=k |
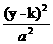 - -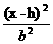 =1 =1 |
(h,±c+h) |
y=±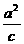 +k +k |
x=h y=k |
|
|
抛物线 |
(y-k)2=2p(x-h) |
(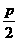 +h,k) +h,k) |
x=-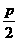 +h +h |
y=k |
|
(y-k)2=-2p(x-h) |
(-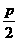 +h,k) +h,k) |
x=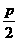 +h +h |
y=k |
|
|
(x-h)2=2p(y-k) |
(h, 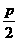 +k) +k) |
y=-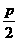 +k +k |
x=h |
|
|
(x-h)2=-2p(y-k) |
(h,- 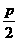 +k) +k) |
y=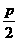 +k +k |
x=h |
4.圆锥曲线的统一定义
平面内的动点P(x,y)到一个定点F(c,0)的距离与到不通过这个定点的一条定直线l的距离之 比是一个常数e(e>0),则动点的轨迹叫做圆锥曲线.
其中定点F(c,0)称为焦点,定直线l称为准线,正常数e称为离心率.
当0<e<1时,轨迹为椭圆
当e=1时,轨迹为抛物线
当e>1时,轨迹为双曲线
3.椭圆、双曲线和抛物线
椭圆、双曲线和抛物线的基本知识见下表.
 |
椭 圆 |
双曲线 |
抛物线 |
|||
|
轨迹条件 |
点集:({M||MF1+|MF2|=2a,|F 1F2|<2a= |
点集:{M||MF1|-|MF2|. =±2a,|F2F2|>2a}. |
点集{M| |MF|=点M到直线l的距离}. |
|||
|
圆 形 |
|
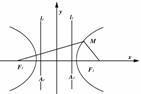 |
 |
|||
|
标准方程 |
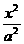 + +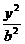 =1(a>b>0) =1(a>b>0) |
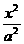 - -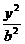 =1(a>0,b>0) =1(a>0,b>0) |
y2=2px(p>0) |
|||
|
顶 点 |
A1(-a,0),A2(a,0); B1(0,-b),B2(0,b) |
A1(0,-a),A2(0,a) |
O(0,0) |
|||
|
轴 |
对称轴x=0,y=0 长轴长:2a 短轴长:2b |
对称轴x=0,y=0 实轴长:2a 虚轴长:2b |
对称轴y= |
|||
|
焦 点 |
F1(-c,0),F2(c,0) 焦点在长轴上 |
F1(-c,0),F2(c,0) 焦点在实轴上 |
F(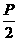 ,0) ,0)焦点对称轴上 |
|||
|
焦 距 |
|F1F2|=2c, c= 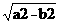 |
|F1F2|=2c, c= 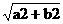 |
|
|||
|
准 线 |
x=±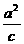 准线垂直于长轴,且在椭圆外. |
x=±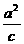 准线垂直于实轴,且在两顶点的内侧. |
x=-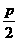 准线与焦点位于顶点两侧,且到顶点的距离相等. |
|||
|
离心率 |
e=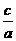 ,0<e<1 ,0<e<1 |
e=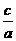 ,e>1 ,e>1 |
e=1 |
2.圆
圆的定义
点集:{M||OM|=r},其中定点O为圆心,定长r为半径.
圆的方程
(1)标准方程
圆心在c(a,b),半径为r的圆方程是
(x-a)2+(y-b)2=r2
圆心在坐标原点,半径为r的圆方程是
x2+y2=r2
(2)一般方程
当D2+E2-4F>0时,一元二次方程
x2+y2+Dx+Ey+F=0
叫做圆的一般方程,圆心为(-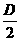 ,-
,-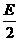 ,半径是
,半径是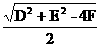 .配方,将方程x2+y2+Dx+Ey+F=0化为
.配方,将方程x2+y2+Dx+Ey+F=0化为
(x+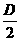 )2+(y+
)2+(y+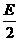 )2=
)2=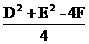
当D2+E2-4F=0时,方程表示一个点
(-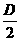 ,-
,-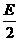 );
);
当D2+E2-4F<0时,方程不表示任何图形.
点与圆的位置关系 已知圆心C(a,b),半径为r,点M的坐标为(x0,y0),则
|MC|<r 点M在圆C内,
点M在圆C内,
|MC|=r 点M在圆C上,
点M在圆C上,
|MC|>r 点M在圆C内,
点M在圆C内,
其中|MC|=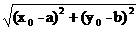 .
.
(3)直线和圆的位置关系
①直线和圆有相交、相切、相离三种位置关系
直线与圆相交 有两个公共点
有两个公共点
直线与圆相切 有一个公共点
有一个公共点
直线与圆相离 没有公共点
没有公共点
②直线和圆的位置关系的判定
(i)判别式法
(ii)利用圆心C(a,b)到直线Ax+By+C=0的距离d=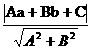 与半径r的大小关系来判定.
与半径r的大小关系来判定.
1.方程的曲线
在平面直角坐标系中,如果某曲线C(看作适合某种条件的点的集合或轨迹 )上的点与一个二元方程f(x,y)=0的实数解建立了如下的关系:
(1)曲线上的点的坐标都是这个方程的解;
(2)以这个方程的解为坐标的点都是曲线上的点.那么这个方程叫做曲线的方程;这条曲线叫 做方程的曲线.
点与曲线的关系 若曲线C的方程是f(x,y)=0,则点P0(x0,y0)在曲线C上 f(x0,y 0)=0;
f(x0,y 0)=0;
点P0(x0,y0)不在曲线C上 f(x0,y0)≠0
f(x0,y0)≠0
两条曲线的交点 若曲线C1,C2的方程分别为f1(x,y)=0,f2(x,y)=0,则
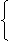 f1(x0,y0)=0
f1(x0,y0)=0
点P0(x0,y0)是C1,C2的交点
f2(x0,y0) =0
方程组有n个不同的实数解,两条曲线就有n个不同的交点;方程组没有实数解,曲线就没有 交点.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com