
题目列表(包括答案和解析)
13.(人教A版必修2第135页B组第3题)
已知点 与两个定点
与两个定点 ,
, 的距离的比为
的距离的比为 ,求点
,求点 的轨迹方程.
的轨迹方程.
变式1:(2006年四川卷)已知两定点 ,
, ,如果动点
,如果动点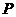 满足
满足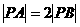 ,则点
,则点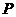 的轨迹所包围的面积等于( )
的轨迹所包围的面积等于( )
A. B.
B. C.
C. D.
D.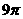
解:设点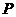 的坐标是
的坐标是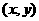 .由
.由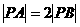 ,得
,得 ,化简得
,化简得 ,∴点
,∴点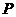 的轨迹是以(2,0)为圆心,2为半径的圆,∴所求面积为
的轨迹是以(2,0)为圆心,2为半径的圆,∴所求面积为 ,故选(B).
,故选(B).
变式2:(2004年全国卷)由动点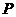 向圆
向圆 引两条切线
引两条切线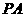 、
、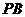 ,切点分别为
,切点分别为 、
、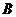 ,
, =600,则动点
=600,则动点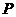 的轨迹方程是 .
的轨迹方程是 .
解:设 .∵
.∵ =600,∴
=600,∴ =300.∵
=300.∵ ,∴
,∴ ,∴
,∴ ,化简得
,化简得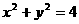 ,∴动点
,∴动点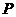 的轨迹方程是
的轨迹方程是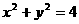 .
.
变式3:(2003年北京春季卷)设 为两定点,动点
为两定点,动点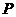 到
到 点的距离与到
点的距离与到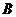 点的距离的比为定值
点的距离的比为定值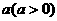 ,求
,求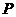 点的轨迹.
点的轨迹.
解:设动点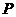 的坐标为
的坐标为 .由
.由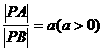 ,得
,得 ,
,
化简得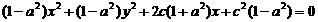 .
.
当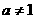 时,化简得
时,化简得 ,整理得
,整理得 ;
;
当 时,化简得
时,化简得 .
.
所以当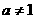 时,
时,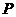 点的轨迹是以
点的轨迹是以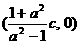 为圆心,
为圆心, 为半径的圆;
为半径的圆;
当 时,
时,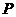 点的轨迹是
点的轨迹是 轴.
轴.
12.(人教A版必修2 第145页B组第2题)
已知点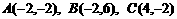 ,点
,点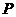 在圆
在圆 上运动,求
上运动,求 的最大值和最小值.
的最大值和最小值.
变式1:(2006年湖南卷)圆 上的点到直线
上的点到直线 的最大距离与最小距离的差是( )
的最大距离与最小距离的差是( )
A.36
B.18
C. D.
D.
解:∵圆 的圆心为(2,2),半径
的圆心为(2,2),半径 ,∴圆心到直线的距离
,∴圆心到直线的距离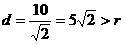 ,∴直线与圆相离,∴圆上的点到直线的最大距离与最小距离的差是
,∴直线与圆相离,∴圆上的点到直线的最大距离与最小距离的差是 ,故选(C).
,故选(C).
变式2:已知 ,
, ,点
,点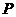 在圆
在圆 上运动,则
上运动,则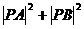 的最小值是 .
的最小值是 .
解:设 ,则
,则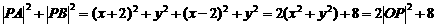 .设圆心为
.设圆心为 ,则
,则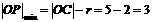 ,∴
,∴ 的最小值为
的最小值为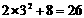 .
.
变式3:已知点 在圆
在圆 上运动.
上运动.
(1)求 的最大值与最小值;(2)求
的最大值与最小值;(2)求 的最大值与最小值.
的最大值与最小值.
解:(1)设 ,则
,则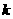 表示点
表示点 与点(2,1)连线的斜率.当该直线与圆相切时,
与点(2,1)连线的斜率.当该直线与圆相切时,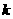 取得最大值与最小值.由
取得最大值与最小值.由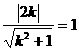 ,解得
,解得 ,∴
,∴ 的最大值为
的最大值为 ,最小值为
,最小值为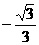 .
.
(2)设 ,则
,则 表示直线
表示直线 在
在 轴上的截距. 当该直线与圆相切时,
轴上的截距. 当该直线与圆相切时, 取得最大值与最小值.由
取得最大值与最小值.由 ,解得
,解得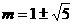 ,∴
,∴ 的最大值为
的最大值为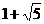 ,最小值为
,最小值为 .
.
11.(北师大版必修2第101页例8)
判断圆 与圆
与圆 的位置关系,并画出图形.
的位置关系,并画出图形.
变式1:(1995年全国卷)圆 和圆
和圆 的位置关系是( )
的位置关系是( )
A.相离 B.外切 C.相交 D.内切
解:∵圆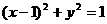 的圆心为
的圆心为 ,半径
,半径 ,圆
,圆 的圆心为
的圆心为 ,半径
,半径 ,∴
,∴ .∵
.∵ ,∴两圆相交,故选(C).
,∴两圆相交,故选(C).
变式2:若圆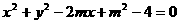 与圆
与圆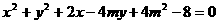 相切,则实数
相切,则实数 的取值集合是
.
的取值集合是
.
解:∵圆 的圆心为
的圆心为 ,半径
,半径 ,圆
,圆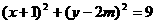 的圆心为
的圆心为 ,半径
,半径 ,且两圆相切,∴
,且两圆相切,∴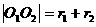 或
或 ,∴
,∴ 或
或 ,解得
,解得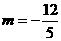 或
或 ,或
,或 或
或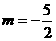 ,∴实数
,∴实数 的取值集合是
的取值集合是 .
.
变式3:求与圆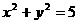 外切于点
外切于点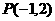 ,且半径为
,且半径为 的圆的方程.
的圆的方程.
解:设所求圆的圆心为 ,则所求圆的方程为
,则所求圆的方程为 .∵两圆外切于点
.∵两圆外切于点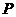 ,∴
,∴ ,∴
,∴ ,∴
,∴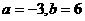 ,∴所求圆的方程为
,∴所求圆的方程为 .
.
10.(北师大版必修2第117页A组 第14题)
已知直线 和圆
和圆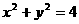 ,判断此直线与已知圆的位置关系.
,判断此直线与已知圆的位置关系.
变式1:(2006年安徽卷)直线 与圆
与圆 没有公共点,则
没有公共点,则 的取值范围是( )
的取值范围是( )
A. B.
B. C.
C. D.
D.
解:依题意有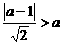 ,解得
,解得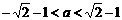 .∵
.∵ ,∴
,∴ ,故选(A).
,故选(A).
变式2:(2006年湖北卷)若直线 与圆
与圆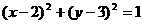 有两个不同的交点,则
有两个不同的交点,则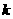 的取值范围是
.
的取值范围是
.
解:依题意有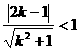 ,解得
,解得 ,∴
,∴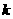 的取值范围是
的取值范围是 .
.
变式3:若直线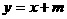 与曲线
与曲线 有且只有一个公共点,求实数
有且只有一个公共点,求实数 的取值范围.
的取值范围.
解:∵曲线 表示半圆
表示半圆 ,∴利用数形结合法,可得实数
,∴利用数形结合法,可得实数 的取值范围是
的取值范围是 或
或 .
.
9.(人教A版必修2 第144页 A组 第5题)
求直线 被圆
被圆 截得的弦
截得的弦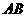 的长.
的长.
变式1:(1999年全国卷)直线 截圆
截圆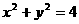 得的劣弧所对的圆心角为( )
得的劣弧所对的圆心角为( )
A.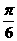 B.
B. C.
C.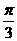 D.
D.
解:依题意得,弦心距 ,故弦长
,故弦长 ,从而△OAB是等边三角形,故截得的劣弧所对的圆心角为
,从而△OAB是等边三角形,故截得的劣弧所对的圆心角为 ,故选(C).
,故选(C).
变式2:(2006年天津卷)设直线 与圆
与圆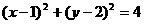 相交于
相交于 、
、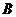 两点,且弦
两点,且弦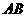 的长为
的长为 ,则
,则 .
.
解:由弦心距、半弦长、半径构成直角三角形,得 ,解得
,解得 .
.
变式3:已知圆 ,直线
,直线 .
.
(1)求证:不论 取什么实数,直线
取什么实数,直线 与圆
与圆 恒交于两点;
恒交于两点;
(2)求直线 被圆
被圆 截得的弦长最小时
截得的弦长最小时 的方程.
的方程.
解:(1)∵直线 恒过定点
恒过定点 ,且
,且 ,∴点
,∴点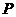 在圆内,∴直线
在圆内,∴直线 与圆
与圆 恒交于两点.
恒交于两点.
(2)由平面几何性质可知,当过圆内的定点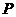 的直线
的直线 垂直于
垂直于 时,直线
时,直线 被圆
被圆 截得的弦长最小,此时
截得的弦长最小,此时 ,∴所求直线
,∴所求直线 的方程为
的方程为 即
即 .
.
8.(人教A版必修2第144页A组 3)
求以 为圆心,并且与直线
为圆心,并且与直线 相切的圆的方程.
相切的圆的方程.
变式1:(2006年重庆卷)过坐标原点且与圆 相切的直线的方程为( )
相切的直线的方程为( )
A. 或
或 B.
B. 或
或
C. 或
或 D.
D. 或
或
解:设直线方程为 ,即
,即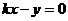 .∵圆方程可化为
.∵圆方程可化为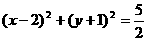 ,∴圆心为(2,-1),半径为
,∴圆心为(2,-1),半径为 .依题意有
.依题意有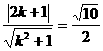 ,解得
,解得 或
或 ,∴直线方程为
,∴直线方程为 或
或 ,故选(A).
,故选(A).
变式2:(2006年湖北卷)已知直线 与圆
与圆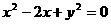 相切,则
相切,则 的值为 .
的值为 .
解:∵圆 的圆心为(1,0),半径为1,∴
的圆心为(1,0),半径为1,∴ ,解得
,解得 或
或 .
.
变式3:求经过点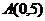 ,且与直线
,且与直线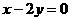 和
和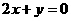 都相切的圆的方程.
都相切的圆的方程.
解:设所求圆的方程为 ,则
,则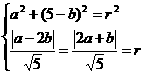 ,
,
解得 或
或 ,∴圆的方程为
,∴圆的方程为 或
或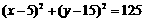 .
.
7.(北师大版必修2 第118页B组第2题)
光线自点 射到点
射到点 后被
后被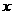 轴反射,求反射光线所在直线的方程.
轴反射,求反射光线所在直线的方程.
变式1:一条光线从点 射出,经
射出,经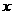 轴反射,与圆
轴反射,与圆 相切,则反射光线所在直线的方程是 .
相切,则反射光线所在直线的方程是 .
解:依题意得,点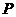 关于
关于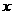 轴的对称点
轴的对称点 在反射光线所在的直线上,故可设反射光线所在直线的方程为
在反射光线所在的直线上,故可设反射光线所在直线的方程为 ,即
,即 .由反射光线与圆相切得
.由反射光线与圆相切得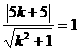 ,解得
,解得 或
或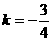 ,∴反射光线所在直线的方程是
,∴反射光线所在直线的方程是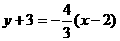 或
或 ,即
,即 或
或 .
.
变式2:(2003年全国卷)已知长方形的四个顶点 、
、 、
、 和
和 ,一质点从
,一质点从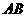 的中点
的中点 沿与
沿与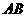 夹角为
夹角为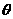 的方向射到
的方向射到 上的点
上的点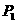 后,依次反射到
后,依次反射到 、
、 和
和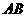 上的点
上的点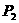 、
、 和
和 (入射角等于反射角).设
(入射角等于反射角).设 的坐标为
的坐标为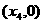 .若
.若 ,则
,则 的取值范围是( )
的取值范围是( )
A. B.
B.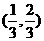 C.
C. D.
D.
解:用特例法,取 ,则
,则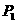 、
、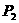 、
、 、
、 分别为
分别为 、
、 、
、 、
、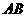 的中点,此时
的中点,此时 .依题意,包含
.依题意,包含 的选项(A)(B)(D)应排除,故选(C).
的选项(A)(B)(D)应排除,故选(C).
变式3:已知点 ,在直线
,在直线 上求一点P,使
上求一点P,使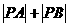 最小.
最小.
解:由题意知,点A、B在直线 的同一侧.由平面几何性质可知,先作出点
的同一侧.由平面几何性质可知,先作出点 关于直线
关于直线 的对称点
的对称点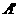 ,然后连结
,然后连结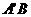 ,则直线
,则直线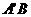 与
与 的交点P为所求.事实上,设点
的交点P为所求.事实上,设点 是
是 上异于P的点,则
上异于P的点,则 .
.
设 ,则
,则 ,解得
,解得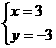 ,∴
,∴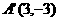 ,∴直线
,∴直线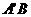 的方程为
的方程为 .由
.由 ,解得
,解得 ,∴
,∴ .
.
6.(人教A版必修2 第110页A组第3题)
已知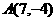 ,
, ,求线段
,求线段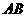 的垂直平分线的方程.
的垂直平分线的方程.
变式1:已知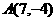 关于直线
关于直线 的对称点为
的对称点为 ,则直线
,则直线 的方程是( )
的方程是( )
A. B.
B.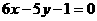 C.
C. D.
D.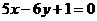
解:依题意得,直线 是线段
是线段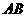 的垂直平分线.∵
的垂直平分线.∵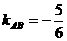 ,∴
,∴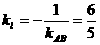 ,∵
,∵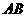 的中点为(1,1),∴直线
的中点为(1,1),∴直线 的方程是
的方程是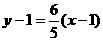 即
即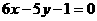 ,故选(B).
,故选(B).
变式2:已知圆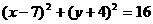 与圆
与圆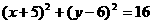 关于直线
关于直线 对称 ,则直线
对称 ,则直线 的方程是
.
的方程是
.
解:依题意得,两圆的圆心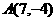 与
与 关于直线
关于直线 对称,故直线
对称,故直线 是线段
是线段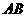 的垂直平分线,由变式1可得直线
的垂直平分线,由变式1可得直线 的方程为
的方程为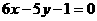 .
.
变式3:求点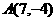 关于直线
关于直线 的对称点
的对称点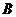 的坐标.
的坐标.
解:设 .由
.由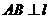 ,且
,且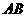 的中点在直线
的中点在直线 上,得
上,得 ,解得
,解得 ,∴
,∴ .
.
5.(北师大版必修2 第117页A组第7题)
若直线 和直线
和直线 垂直,求
垂直,求 的值.
的值.
变式1:(1987年上海卷)若直线 与直线
与直线 平行但不重合,则
平行但不重合,则 等于( )
等于( )
A.-1或2
B.-1 C.2
D.
解:∵ ,∴
,∴ 且
且 ,∴
,∴ 且
且 ,解得
,解得 ,故选(B).
,故选(B).
变式2:(2005年北京春季卷)“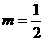 ”是“直线
”是“直线 与直线
与直线 相互垂直”的( )
相互垂直”的( )
A.充分必要条件 B.充分而不必要条件
C.必要而不充分条件 D.既不充分也不必要条件
解:由 或
或 ,知由
,知由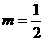 可推出
可推出 ,但由
,但由 推不出
推不出 ,故
,故 是
是 的充分不必要条件,故选(B).
的充分不必要条件,故选(B).
变式3:设直线 与圆
与圆 相交于点
相交于点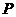 、
、 两点,
两点, 为坐标原点,且
为坐标原点,且 ,求
,求 的值.
的值.
解:∵圆 经过原点
经过原点 ,且
,且 ,∴
,∴ 是圆的直径,∴圆心(1,-2)在直线
是圆的直径,∴圆心(1,-2)在直线 上,∴
上,∴ .
.
4.(北师大版必修2 第117页A组第10题)
求过点 ,且与直线
,且与直线 平行的直线的方程.
平行的直线的方程.
变式1:(2005年全国卷)已知过点 和
和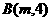 的直线与直线
的直线与直线 平行,则
平行,则 的值为( )
的值为( )
A.0 B.-8 C.2 D.10
解:依题意有 ,解得
,解得 ,故选(B).
,故选(B).
变式2:与直线 平行,且距离等于
平行,且距离等于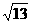 的直线方程是 .
的直线方程是 .
解:设所求直线方程为 ,则
,则 ,解得
,解得 或
或 ,∴直线方程为
,∴直线方程为 或
或 .
.
变式3:已知三条直线 不能构成三角形,求实数
不能构成三角形,求实数 的取值集合.
的取值集合.
解:依题意,当三条直线中有两条平行或重合,或三条直线交于一点时,三条直线不能构成三角形,故 或
或 或
或 ,∴实数
,∴实数 的取值集合是
的取值集合是 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com